1. HOME > 構造力学の基礎 > 固有値解析法について

固有値解析法について

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

固有値解析法は多質点系の振動解析や座屈モードの解析に利用される手法である。

ここでは，例えば振動の固有値問題を考える。多質点系の振動方程式から、以下のように固有値問題の式は解を深める。

([K] －λ[M]){u}={0} (1)

の解法について論じる。

ここで，[K]: 剛性マトリクス、[M]:質量マトリクスである。

(1)式を満たすλと，{0}でないベクトル{u}を求める。このようなλを一般固有値問題の固有値，{u}をλに対する固有ベクトルという。1)式は連立方程式とみなすことができる。

すなわち，([K] －λ[M])が係数マトリクス，{u}は未知数，{0}が定数項と考える。

定数項が{0}というのは，連立１次方程式では特殊な形（同次形）であって，そのような連立１次方程式が{0}以外の解を持つための条件は，「係数マトリクスの行列式の値が0であること｣であるから，

|[K] －λ[M]| = 0 (2)

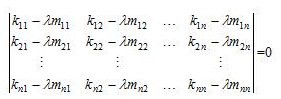(3)

(3)式を展開すると，λに対するn次の代数方程式

が得られる。これを特性方程式という。

一般に次の代数方程式には個の解があるから，次の固有値問題には個の固有値があるということがわかる。特性方程式を解いてλが決まれば，それを(1)式に代入し，対応する固有ベクトル{u}を求めることができる。

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

記事を書いた人

ハナダユキヒロ／建築学生が学ぶ「構造力学」

難解な構造力学、建築構造の用語を分かりやすく解説する専門家。高等専門学校在学中から建築学生が学ぶ「構造力学」を運営。その後、国立大学大学院⇒組織設計事務所⇒弊サイト運営に従事している。

著書：「わかる構造力学/工学社」、「わかる構造力学 改訂版/工学社」

LINEで質問したい方はこちら　⇒　【好評】管理人にLINEで質問してみよう

一般的な解法

上記の方法で計算すれば，原理的にはどんな問題も解けるはずである。しかし，実際は，

･必要演算回数が多い（特に次数nが大きい場合に不利）

･丸め誤差の影響を受けやすい（特に次数nが大きい場合に深刻）

という欠点があるため，極めて小規模な問題にしか適用できない。

そこで，固有値問題の数学的性質をうまく利用して，もっと能率的かつ，制度よく計算する方法が考察されている。

代表的なものに，

・ Jacobi法 ：原理も計算手順も簡単である。全部の固有値，固有ベクトルが同時に求められる。中規模用のプログラムの自作に最適である。

・ Householder法：Jacobi法より複雑ではあるが，概して能率はよい。計算センターのライブラリ，プログラムなどにおいて，固有値問題の標準的解法として使用されている。

がある。

一般的固有値問題を標準固有値問題に変換する方法

上記の方法はいずれも標準固有値問題

の解法であり，一般固有値問題

を解くには，それをまず標準固有値問題に変換する必要がある。それには，質量マトリクス[M]をコレスキー分解（LU分解の特別な場合）し，

[L]の逆マトリクス[L]-1を(6)式の左から乗ずる。

ここで，

とおく。また、

(10) 式を(8)式へ代入すれば，

となり，標準固有値問題と同じ形になる。したがって，計算手順として

を作る。その固有値λ，固有ベクトル{x}を求める。

とすればいい。一般に，「転置マトリクスの逆マトリクス」と「逆マトリクスの転置マトリクス」は等しいので

したがって，先に[L] -1が計算してあれば，それを転置マトリクスにするだけで，[L T]-1は得られる。

大規模固有値問題の解法

以上のような方法で次数（自由度）100ぐらいまでの問題を解くことができる。

簡単な問題ならばそれでも済むが，有限要素法ではもっと大きい問題を解きたいことがある。

そのためには，3）のような一般的解法では無理で，有限要素法のマトリクスの特殊性を利用して，大規模な問題にまで適用できるような方法を工夫する必要がある。

そのような解法としては，

a） べき乗法の系統の解法：べき乗法，逆反復法

b） 同時反復法：サブスペース法，Jennings法

c） 三角対角化の改良版：村田法，帯田Givens法

d） Lanczos法

e） 行列式法，Strum法

がある。ここでは，a）について簡単に説明する。

a-1）べき乗法

標準固有値問題

を解きたい場合，適当なベクトル{x}0をとる。{x}0≠{0}

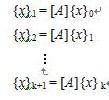
よって，ベクトル列

を作れば，それが[A]の絶対値最大の固有値に対応する固有ベクトルに収束するというのが，べき乗法の原型である。

固有値は，Rayleigh商

により近似計算できる。例として，

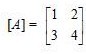
のとき

で出発すれば，

これらより，Rayleigh商をとると，

固有値は約5.372であることがわかる。

固有値の推定にはRayleigh商を用いるのが精度的にも有利であるが，もっと手軽な方法としては，成分の比率をとってもよい。

「成分の比率の最大値と最小値の間に真の固有値がある」という性質があるので，計算精度を手軽にチェックできるという利点がある。

上記の例に適用すると，

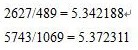
であるから，この間に真の固有値があることがわかる。特性方程式を用いて厳密な固有値（大きいほう）を計算してみると，

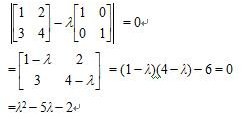
であるから，確かに上記の範囲内に入っている。

a-2）べき乗の根拠

[A]の固有値を

とし，それに対する固有ベクトルを

とする。ベクトル{x}0は（特殊な場合を除き）固有ベクトルの1次結合，

の形で表すことができる。Cnはスカラーである。上式に左から[A]をかけると，

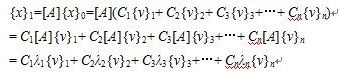
以下，同様にして，

となることがわかる。固有値の番号を絶対値の大きい順に付けてあるとして，

とすると，kを大きくしていく順に従って，(25)式の右辺第一項が卓越するようになり，k→∞のとき，

となる。上式から，収束の速さが主として，21/λλすなわち，「最大固有値と2番目の固有値の比」で決まることがわかる。

a-3）逆反復法

べき乗法を適用すると、最大固有値が求められるが、振動、座屈の問題の場合最も関心があるのは、最小固有値である。

それには標準固有値問題[A]{x} = λ{x}の両辺に左からλ-1 [A]-1をかけて，

に変形し、

の形でべき乗法を適用すればよい。固有値はReyleigh商の逆数

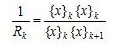
より計算できる（固有ベクトルはそのまま）。このような方法を逆反復法という。実際には、逆マトリクス[A]-1をつくることは時間がかかり、不効率なので、代わりに連立1次方程式

を解いて、{x}k+1を計算する。

一般固有値問題、(1)式の場合には、(30)式の代わりに、

を用いる。詳しく述べると、

以上のように，一般固有値問題の{x}k+1を求めることができる。

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

▼スポンサーリンク▼

【初回資料が今だけ無料！】1日約13円で情報をアップデート！

有料メルマガを無料で見てみませんか？⇒　忙しい社会人、学生のためのビルディング・アップデート

更新情報

• 当サイトでは、ほぼ毎日、記事更新・追加を行っております。


• 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。


• 新着記事一覧

プロフィール

• 
• 略歴▼
• 名前　ハナダユキヒロ/MITUME lab代表.
• 2010年　弊サイトを開設
• 2010～2017年　国立大学大学院修了
• 2017年12月に当HPが書籍化。
• 「わかる構造力学」
• 2022年4月に「わかる構造力学」の改訂版出版。
• 「わかる構造力学(改訂版)」


• 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。


• 当サイトの目的▼
• 建築学生が学ぶ「構造力学」の目的


• とりあえず10記事▼
• 初めましての方に10記事用意しました


• おすすめ書籍紹介▼
• ハナダユキヒロが建築関連書籍の良書を選びました

建築の本、紹介します。▼

▼【好評！】管理人おすすめ▼

• あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！

同じカテゴリの記事一覧