- HOME > 二級建築士の問題 構造解説 > 梁の応力から荷重を計算する問題の解説
梁の応力から荷重を計算する問題の解説
【管理人おすすめ!】セットで3割もお得!大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集&図解集セット(※既に26人にお申込みいただきました!)
梁の応力は荷重条件、梁のスパン、支点条件が既知であるとき、力のつりあい(ΣV=0、ΣH=0、ΣM=0)を計算して求めます。
応力は部材の断面内に生じる力で、部材を曲げる力(曲げモーメント)、ずらす力(せん断力)、引っ張るまたは押す力(軸方向力)の3つが作用します。
応力は断面内に生じるため、部材を任意の位置で仮想的に切断し、切断面に前述した3つの応力が生じていると仮定し、外力、反力との釣り合いから求めます。
梁の応力と荷重の関係
では、具体的な問題から梁の応力の計算を学びましょう。
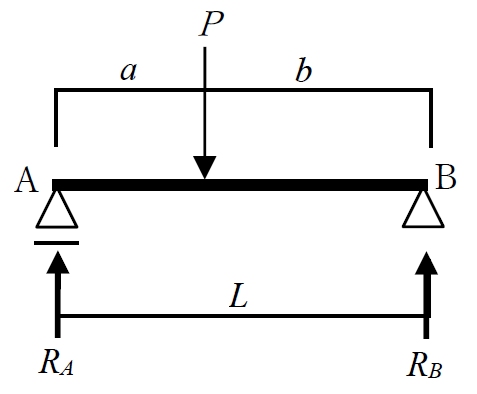
基本的な考え方は反力の求め方と同じです。ただし応力は部材断面に生じる力なので、まずは部材を切断して作用する応力を仮定します。
切断する位置は支点から任意の点(x)としますが、荷重の作用点を境に応力が変化する可能性を考慮して切断します。
よって、点Aを原点とするとき「0からa」と「aからL」の任意の点xで切断します。
このとき切断面には正の向きの応力が作用すると仮定します。水平方向の荷重は無いので、梁を引っ張る、押す力(軸力)は0とします。
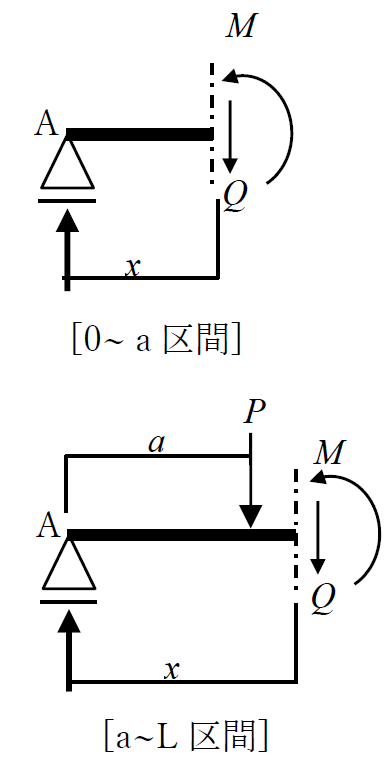
なお、点Bを原点として同様に切断してもよいです。その場合「0からb」と「bからL」の任意の点xで切断します。
梁を任意の点で切断しても応力と荷重、反力はつりあうので、ΣH=0、ΣV=0、ΣM=0のつりあいを考えれば良いのです。
※水平力は無いのでΣH=0は省略します。「0からa」と「aからL」の区間と順番に計算します。
[0からaの区間]
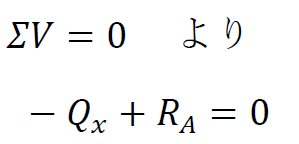
計算過程は省略しますが、本例題の反力はRA=Pb/L、RB=Pb/Lです。よって、
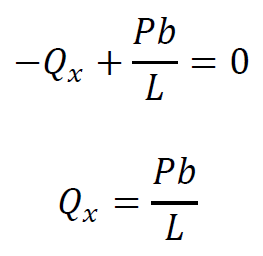
です。次にモーメントのつりあいを考えます。点xでの曲げモーメントを求めたいので、点xが中心となるようモーメントを求めましょう。
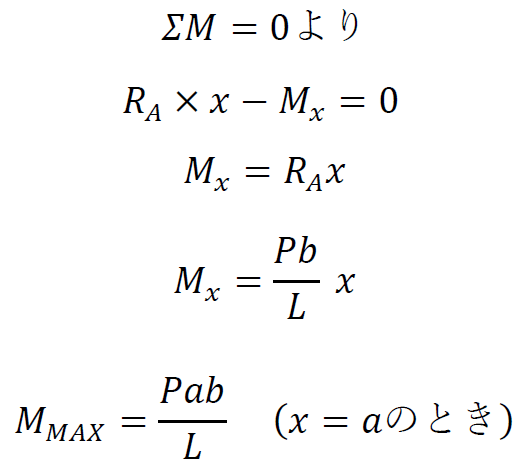
となります。 aからLの区間も同様の手順で応力を求めます。
[aからLの区間]
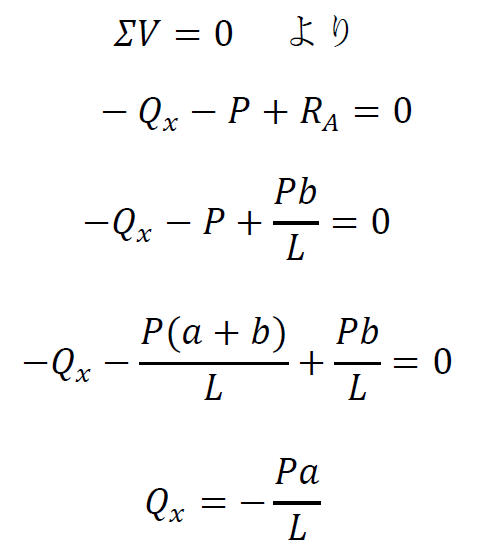
です。
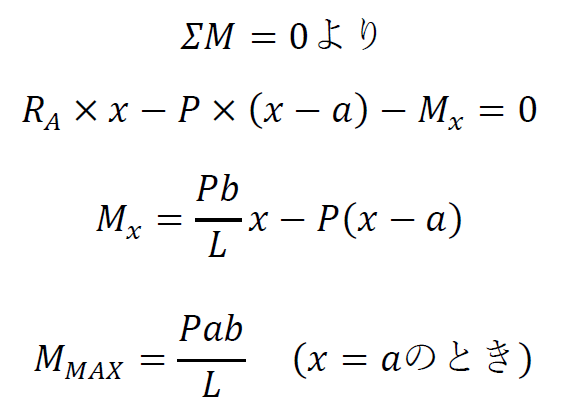
です。 以上より、せん断力は0からa区間まではPb/L(正のせん断力)が作用し、aからL区間では-Pa/L(負のせん断力)となります。
また曲げモーメントは支点では0となり、x=aのとき最大値となります。
逆に、梁の応力(曲げモーメント、せん断力)が既知であれば、その他の諸条件(たとえば荷重)を算定できます。
実際、建築士試験の問題では、梁の曲げモーメントが既知である状態から、梁の支点反力やせん断力を求める問題などが出題されます。
建築士試験の例題を解説
実際に下図の例題を解きながら、梁の応力の計算を理解しましょう。下図に示すように、梁に荷重Pが作用しています。
しかし、問題発生。Pの値は与えられていません。その代り、Pの作用位置における曲げモーメントの大きさが分かっています。少し頭を捻らないと解けなさそうです。

上図のようにPが中央でない位置に作用したとき、その反力を求める公式は

です。
今回の場合、a=2mで、b=4mです。Lは全体の長さですから、
です。
よって、左支点の反力Rを算定すると
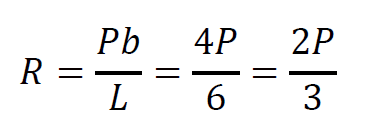
です。
次に曲げモーメントを求めます。曲げモーメントとは、部材を曲げようとする力です。
Pの作用位置における曲げモーメントMは「支点反力×Pまでの距離」で算定できるので、左側支点から考えると
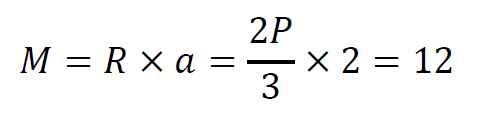
です。あとは、この方程式を解けばPが逆算できるので、
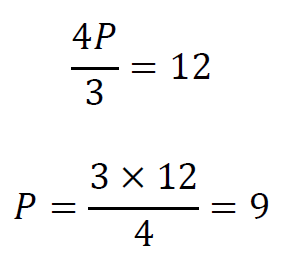
となります。
最後にせん断力を算定します。せん断力とは、部材をずらそうとする応力です。
部材断面に生じるせん断力も力のつり合いで求めます。点C(Pの作用位置)の切断面に生じるせん断力は、支点Aに生じる反力と釣り合うので
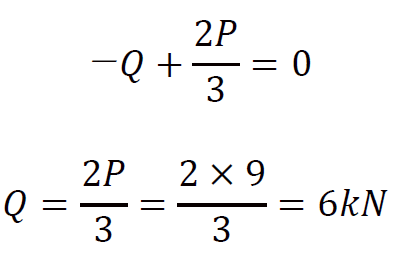
となり、答えは3だとわかります。
まとめ
今回は、梁の応力から荷重、せん断力を計算する問題を解説しました。建築士試験で頻出する問題です。
力のつり合い、梁の反力、応力の算定の基礎が試されます。慣れるまでは同様の問題を解き続けましょう。梁の力のつり合い、応力の計算など下記も参考になります。
集中荷重の作用する単純梁の解き方は?1分でわかる曲げモーメント、せん断力、たわみ、2点集中荷重の計算は?
【管理人おすすめ!】セットで3割もお得!大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集&図解集セット(※既に26人にお申込みいただきました!)
▼スポンサーリンク▼
▼用語の意味知らなくて大丈夫?▼

▼同じカテゴリの記事一覧▼
- 二級建築士試験問題の構造計算とは?1分でわかる問題の種類、解き方、曲げモーメントの関係
- 二級建築士の構造力学は?問題の特徴、覚えるべき公式、独学で合格可能?
- 二級建築士の構造力学は捨てて大丈夫?合格の可能性、構造の試験問題、力学が苦手な人の勉強法
- 二級建築士の構造の勉強法は?独学、問題内容、過去問との関係
- 二級建築士の構造の問題は?必要な公式、過去問の解説、暗記の必要性
- 二級建築士H27 トラスに鉛直力が作用する問題
- 二級建築士H27 ラーメン構造に鉛直、水平力が作用する問題
- 二級建築士H27 I型の断面二次モーメントの算定
- 座屈長さの求め方と例題の計算
- 鉄筋コンクリート柱のせん断補強筋比の考え方と例題
▼カテゴリ一覧▼
- 一級建築士について(まずは、一級建築士を取得するには?絶対取る!と決めた日から始めること3選から)
- 二級建築士の問題 構造解説(H28年)(まずは、二級建築士H28 リップ溝型鋼の断面二次モーメントの算定から)
- 二級建築士の問題 構造解説(H27年)(まずは、二級建築士H28 鉄骨構造に関する不適当な記述を選ぶ問題から)
- 二級建築士の問題 構造解説(H26年)(まずは、二級建築士H26 L型断面の図芯を求める問題から)
▼他の勉強がしたい方はこちら▼
更新情報
- 当サイトでは、ほぼ毎日、記事更新・追加を行っております。
- 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。
- 新着記事一覧
プロフィール

- 略歴▼
- 名前 ハナダユキヒロ/MITUME lab代表.
- 2010年 弊サイトを開設
- 2010~2017年 国立大学大学院修了
- 2017年12月に当HPが書籍化。
- 「わかる構造力学」
- 2022年4月に「わかる構造力学」の改訂版出版。
- 「わかる構造力学(改訂版)」
- 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に向けて
- 「構造力学、構造計算、鋼構造、鉄筋コンクリート造、基礎構造、土質力学、水理学、材料力学、数学の基礎」を分かりやすくお伝えします。
- 当サイトの目的▼
- 建築学生が学ぶ「構造力学」の目的
- とりあえず10記事▼
- 初めましての方に10記事用意しました
- おすすめ書籍紹介▼
- ハナダユキヒロが建築関連書籍の良書を選びました
同じカテゴリの記事一覧
- 二級建築士試験問題の構造計算とは?1分でわかる問題の種類、解き方、曲げモーメントの関係
- 二級建築士の構造力学は?問題の特徴、覚えるべき公式、独学で合格可能?
- 二級建築士の構造力学は捨てて大丈夫?合格の可能性、構造の試験問題、力学が苦手な人の勉強法
- 二級建築士の構造の勉強法は?独学、問題内容、過去問との関係
- 二級建築士の構造の問題は?必要な公式、過去問の解説、暗記の必要性
- 二級建築士H27 トラスに鉛直力が作用する問題
- 二級建築士H27 ラーメン構造に鉛直、水平力が作用する問題
- 二級建築士H27 I型の断面二次モーメントの算定
- 座屈長さの求め方と例題の計算
- 鉄筋コンクリート柱のせん断補強筋比の考え方と例題
- HOME > 二級建築士の問題 構造解説 > 梁の応力から荷重を計算する問題の解説
- 1級の過去問(計算)解説
- 限定メルマガ
- わかる建築構造の用語集・図解集
- 1頁10円!PDF版の学習記事




