1. HOME > 構造力学の基礎 > 断面二次モーメントとは？1分でわかる意味、計算式、h形鋼、公式、たわみとの関係

断面二次モーメントとは？1分でわかる意味、計算式、h形鋼、公式、たわみとの関係

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

断面二次モーメントは、「材料の曲げにくさ（曲げる力に対する抵抗性）」を表します。断面二次モーメントが大きいほど、曲げにくい材料です。今回は断面二次モーメントの意味、計算式、h形鋼、たわみとの関係について説明します。

断面二次モーメントと似た用語の断面係数の意味、たわみの計算は下記が参考になります。

断面係数とは

たわみとは？1分でわかる意味、求め方、公式、単位、記号、計算法

断面二次モーメントとたわみの関係は？1分でわかる意味、計算式、剛性との関係

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

記事を書いた人

ハナダユキヒロ／建築学生が学ぶ「構造力学」

難解な構造力学、建築構造の用語を分かりやすく解説する専門家。高等専門学校在学中から建築学生が学ぶ「構造力学」を運営。その後、国立大学大学院⇒組織設計事務所⇒弊サイト運営に従事している。

著書：「わかる構造力学/工学社」、「わかる構造力学 改訂版/工学社」

LINEで質問したい方はこちら　⇒　【好評】管理人にLINEで質問してみよう

断面二次モーメントとは？

断面二次モーメントは、「材料の曲げにくさ（曲げる力に対する抵抗性）」を表します。

部材の｢曲げにくさ｣は、材料の性質で決まります。ゴムよりも木の方が曲げにくいですし、木よりも鉄の方が曲げにくいです。また部材の形状（H型やI型など）でも曲げにくさは違います。専門的にいうと、下記の値が関係します。

・ヤング係数（材料そのものの固さ。ゴムや木、鉄ごとに値が変わる）

・断面二次モーメント（部材の形による固さの違い。正方形とH形では固さが変わる）

ヤング係数の意味は、下記が参考になります。

ヤング係数ってなに？1分でわかるたった1つのポイント

断面二次モーメントと近い値に、断面係数があります。断面係数については、断面係数とは何か？で説明しています。

断面二次モーメントと、たわみの関係

断面二次モーメントは、曲げモーメントにどの程度耐えられるかを判断する値です。また部材の剛性を計算するとき、振動特性・座屈などあらゆる場面で活躍します。

特に、「たわみの計算」では断面二次モーメントが必要不可欠です。たわみの計算は下記が参考になります。

断面二次モーメントとたわみの関係は？1分でわかる意味、計算式、剛性との関係

たわみとは？1分でわかる意味、求め方、公式、単位、記号、計算法

剛性の意味は下記をご覧ください。

剛性とは？簡単な意味、剛性の計算、単位、強度との違い

断面二次モーメントの公式

一般的に使う断面二次モーメントの公式を下記に整理しました。

長方形　⇒　I=bh³/12

円形　⇒　I=πd⁴/64

円筒形　⇒　I=π(d⁴－d1⁴)/64

ｂは長方形の幅、ｈは高さです。ｄは円形、円筒形の外形、ｄ1は円筒形の内法寸法です。※外径、内法寸法の意味は、下記が参考になります。

外径とは？1分でわかる意味、図、直径との違い、円周の求め方

断面二次モーメントの公式は、下記も参考にしてください。

断面二次モーメントの計算式は？1分でわかる求め方、円、パイプ、i型の計算式

断面二次モーメントの公式の導出

まず初めに、断面二次モーメントの定義から公式を導出します。いきなり公式を覚えるのも良いですが、導出方法を理解することで公式の暗記が不要になります。

断面二次モーメントの定義は、

同様にy軸に関する断面二次モーメントは

よって、図のような長方形のx軸に関する断面二次モーメントは、

です。

次節で学ぶ曲げ応力度を計算するときなどは、部材図心軸に関する断面二次モーメントが重要ですから、図心に関するx軸の断面二次モーメントをIuとすれば、

となります。図心に関するx軸の断面二次モーメントを求めるので、積分範囲は0～b/2です。また、図心x軸に対して対称ですから半分の部材に関して断面二次モーメントを求めれば、その値に2を乗じたものが図心に関するx軸の断面二次モーメントIuです。

図心の意味、断面二次モーメントとの関係は下記をご覧ください。

図心ってなに？図心の求め方と断面一次モーメントの関係

断面二次モーメントと図心の関係は？3分でわかる意味と計算、図心を通らない断面二次モーメントの求め方

軸から離れた位置にある図形の断面二次モーメントの求め方

さて、もう少し一般的な問題について断面二次モーメントを考えてみましょう。次のような任意の物体についての断面二次モーメントを求めます。まず、原点Oとその座標軸xyを考え、さらに、その座標軸がuvだけ平行移動した場合を考えます。

このように、ある任意の物体についてのx軸に関する断面二次モーメントは、定義式から

で、元の座標軸と変化した座標軸の関係から、

と変形することができますね。同様に、y軸に関しても計算すると、

となります。さらに、新しい座標軸を図心を原点（xo,yo）にもつ座標軸とした場合、以上に示した式

となるので、

ですね。以上に示した式は、任意の座標（u,v）に関する断面二次モーメントを求める際に良く用いられる式です。この式も重要ですので、導出方法を理解し、式は暗記してもいいくらいですね。

材料力学の中で、とても重要な概念の1つが｢断面二次モーメント｣です。次章では、実際に断面二次モーメントの計算を行ってさらに、理解しましょう。これまでは、定義式だけの勉強を行ってきましたが、本来は簡便な計算法を用います。その方法で断面二次モーメントを計算し問題に慣れましょう。

例題　Ｈ型断面、トラス梁、ＲＣ梁のＩを算定する

先ほど軸から任意の位置にある図形の断面二次モーメントを求めました。この式は一体いつ使うのでしょうか？

実は、かなり使用する場面があります。例えば、Ｈ型鋼の断面二次モーメントを算定する場合を紹介します。

H形鋼、トラスの意味は下記が参考になります。

Ｈ形鋼とは？1分でわかる意味、規格、寸法、重量、断面係数、材質、用途

トラス構造とは？1分でわかるメリット、デメリット、計算法

Ｈ型断面のＩの算定

Ｈ型断面は下図のように、中立軸が断面の中央にあります。

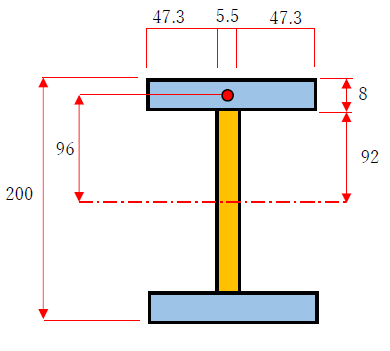
このとき、オレンジ色部分（ウェブといいます）は中立軸に対して丁度真ん中に位置していますので、このＩは

I＝bh³／12＝5.5×(92*2)³／12=2855189

次に、青部分（フランジといいます）のＩを求めます。フランジは中立軸に対して離れた位置にあります。つまり、先ほど勉強した「軸から任意の位置にある図形のＩの求め方」が活きてくるわけです。

もう一度、その公式をおさらいすると、

でした。つまり、フランジ部分のＩを片側だけ計算すると、

これは片側のフランジのＩなので、２倍します。

です。よって、ウェブとフランジ部分のＩを足し合わせてＨ型断面のＩとなります。結果は、

I=14754132+2855189=17609321 mm⁴

ｃｍ4の単位に直すと、

I=1760 cm⁴

です。

実は、このＨ型は構造設計の実務でも良く用いる部材の１つ。Ｈ-200ｘ100ｘ5.5ｘ8というＨ型鋼でした。本当はＲ部分があって、断面がもう少し大きいことから、公称のＩは1810と決まっています。

今回の計算結果とほぼ同じなので、計算結果が正しいことも確認できました。H形鋼の意味、断面二次モーメントは、下記が参考になります。

Ｈ形鋼とは？1分でわかる意味、規格、寸法、重量、断面係数、材質、用途

h形鋼断面の断面二次モーメントは？5分でわかる求め方、弱軸と強軸の違い、一覧

トラス梁のＩの算定

下図のようなトラス梁があります（断面図）。上下弦材にＨ型鋼を用いており、間をつなぐ部材をチャンネル材としました。このトラス材が合理的か否かはひとまず置いといて。

トラス梁のＩを求める方法も、先ほどの方法を用いれば簡単です。さて、トラス梁Ｉは繋ぎ材は考慮しませんから、上下弦材のみのＩを求めます。

なので、Ｈ型鋼　Ｈ-200ｘ100ｘ5.5ｘ8単体のＩは1810cm4です。Ａは8ｘ100ｘ2+5.5ｘ96ｘ2＝2656m㎡。ｙは、1000/2＝500mmです。

となりました。

いかがでしょうか？いかにトラス梁の断面性能が大きいか理解して頂けたと思います。実務でもトラス梁のＩは、上記の計算で求めています。

トラスの意味は、下記が参考になります。

トラス構造とは？1分でわかるメリット、デメリット、計算法

ＲＣ梁の鉄筋を考慮したＩの算定

実はＲＣ梁のＩも簡単に求めることが可能です。中立軸から離れた位置にある鉄筋のＩを考慮するだけです。

詳しくは当ＨＰの「ＲＣ梁の鉄筋を考慮した断面二次モーメントの算定方法について」をご確認ください。

まとめ

今回は断面二次モーメントについて説明しました。意味が理解頂けたと思います。断面二次モーメントは材料の曲げにくさを表す値です。たわみの計算で必要不可欠です。似た用語である断面係数との違いも理解しましょうね。下記も併せて学習しましょう。

断面係数とは

断面二次モーメントの導出方法は？式の意味と考え方、慣性モーメントとの関係

断面二次モーメントと図心の関係は？3分でわかる意味と計算、図心を通らない断面二次モーメントの求め方

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

▼スポンサーリンク▼

【初回資料が今だけ無料！】1日約13円で情報をアップデート！

有料メルマガを無料で見てみませんか？⇒　忙しい社会人、学生のためのビルディング・アップデート

更新情報

• 当サイトでは、ほぼ毎日、記事更新・追加を行っております。


• 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。


• 新着記事一覧

プロフィール

• 
• 略歴▼
• 名前　ハナダユキヒロ/MITUME lab代表.
• 2010年　弊サイトを開設
• 2010～2017年　国立大学大学院修了
• 2017年12月に当HPが書籍化。
• 「わかる構造力学」
• 2022年4月に「わかる構造力学」の改訂版出版。
• 「わかる構造力学(改訂版)」


• 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に向けて


• 「構造力学、構造計算、鋼構造、鉄筋コンクリート造、基礎構造、土質力学、水理学、材料力学、数学の基礎」を分かりやすくお伝えします。


• 当サイトの目的▼
• 建築学生が学ぶ「構造力学」の目的


• とりあえず10記事▼
• 初めましての方に10記事用意しました


• おすすめ書籍紹介▼
• ハナダユキヒロが建築関連書籍の良書を選びました

建築の本、紹介します。▼

▼【好評！】管理人おすすめ▼

• あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！

同じカテゴリの記事一覧

• 断面二次モーメントの導出方法は？式の意味と考え方、慣性モーメントとの関係
• 断面二次モーメントのIxとIyの違いは？1分でわかる意味、使い方、計算方法は？
• 断面二次モーメントと図心の関係は？3分でわかる意味と計算、図心を通らない断面二次モーメントの求め方
• 断面二次モーメントとたわみの関係は？1分でわかる意味、計算式、剛性との関係
• 断面二次モーメントの単位は？1分でわかる意味、読み方、換算方法
• 断面二次モーメントの計算式は？1分でわかる求め方、円、パイプ、i型の計算式
• 断面二次モーメントの足し算とは？1分でわかる意味、引き算、図心を通らない断面の断面二次モーメントは？
• 長方形の断面二次モーメントは？1分でわかる求め方と計算式、向きと方向、幅の関係
• 正方形の断面二次モーメントは？1分でわかる公式、計算、断面係数の公式、長方形との違い
• 円の断面二次モーメントの求め方は？1分でわかる公式、導出方法、計算例