1. HOME > 構造力学の基礎 > 断面係数とは

断面係数とは

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

断面係数とは何でしょうか？『断面』+『係数』という言葉ですから、これは断面に関係することだなと、なんとなく分かります。 実は、こうやって言葉の意味を考えるのは重要です。理系の専門用語１つ決めるために、何十人の偉い先生たちが色々議論をしています。 ですから断面係数という呪文のような言葉も、意味があります。

 

断面係数とは『部材の断面性能を表す値』です。曲げる力（曲げモーメント）に対する強さ・抵抗力と言えます。 今回は、そんな断面係数の意味や断面係数の公式、公式の導出方法について分かりやすく説明していきますね。

ちなみに、下記の項目を理解しておけば、今回の説明がより理解できるはずです。あわせて参考にしてください。

• 断面係数の誘導に必須⇒・断面二次モーメントとは何か？
• 理解すると今回の記事がよりスムーズに読める⇒・梁の曲げ応力度と誘導方法
• 曲げモーメントの意味を理解する⇒・断面力とは何か？

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

記事を書いた人

ハナダユキヒロ／建築学生が学ぶ「構造力学」

難解な構造力学、建築構造の用語を分かりやすく解説する専門家。高等専門学校在学中から建築学生が学ぶ「構造力学」を運営。その後、国立大学大学院⇒組織設計事務所⇒弊サイト運営に従事している。

著書：「わかる構造力学/工学社」、「わかる構造力学 改訂版/工学社」

LINEで質問したい方はこちら　⇒　【好評】管理人にLINEで質問してみよう

断面係数の意味

断面係数は『断面二次モーメント』という係数と密接な関係があります。 なぜなら、断面係数は断面二次モーメントから求めた式だからです。 つまり断面係数≒断面二次モーメントと言えるくらい似ています。両者とも曲げモーメントにどれだけ抵抗できるか？を意味しています。※断面二次モーメントについては下記の記事が参考になります。

断面二次モーメントとは何か？

一方で断面係数と断面二次モーメントは、構造力学（構造計算）で全く違う使い方をします。断面係数は『応力度算定』、断面二次モーメントは 『たわみの算定』に用いられます。では、実際に断面係数の公式をみていきましょう。

断面係数の公式

まずは構造力学で良く用いる断面係数の公式を紹介します。この後、公式の導出を２つの方法について説明を行いますね。

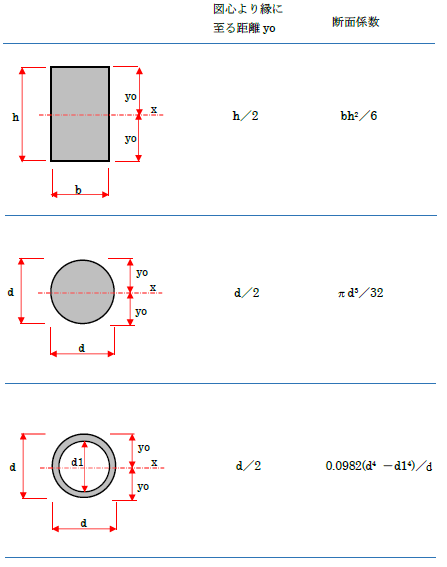
こんな図形も考えられますね。

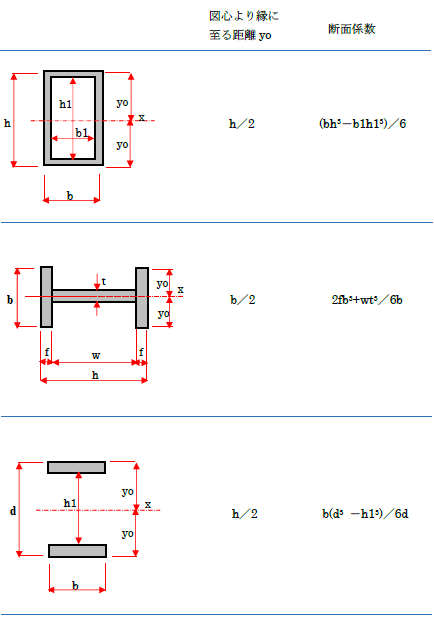
断面係数　矩形断面公式の導出　一般的な方法

前述したように、断面係数Ｚとは簡単に言えば、「曲げモーメントにどれだけ抵抗できるか？」示す値です。この断面係数の大本の式は、当サイトの曲げ応力度の誘導で示しています。下式をみてください。

σ＝Ｍ×y／I

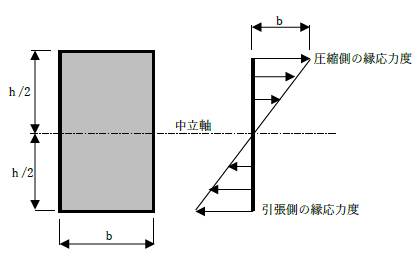
このとき、曲げ応力度の縁応力度は下図に示すように引張側、圧縮側にそれぞれ

• σ₁＝Ｍ×y₁／I
• σ₂＝Ｍ×y₂／I

となりました。

上式を少し簡略化して、σ＝Ｍ／Ｚとしたとき、「Ｚ」を断面係数といいます。つまりＺは、

Ｚ＝Ｉ／ｙ

です。

• σ＝Ｍ/Ｚ

という式を導きました。この式を見て明らかなように、断面係数Ｚが大きければ、曲げ応力度σが小さくなります。また、梁せい（梁の高さ）が大きいほど断面二次モーメントも大きくなります。同様に、断面係数も大きくなるのです。

さて、四角形断面を考えると断面二次モーメントＩ＝bh³/12ですから、断面係数Ｚは

• Ｚ＝I/y＝( bh³/12)/h/2＝bh²/6

となります。

σ＝Ｍ/Ｚを変形して、

Ｍ＝σＺ

です。

σは曲げ応力度ですが、例えば、鋼（スチール）の長期許容曲げ応力度fb＝156です。短期許容応力度fb＝235です。（本来、許容曲げ応力度は横座屈の低減がありますが、ここでは割愛することにします。）

つまり

Ｍ＝σ×Z＝f_b×Z

という式に置き換えることもできます。Maは許容曲げ応力度です。実務では、部材の応力を求めた時点でざっくりMaを上式で計算し、作用応力と見合う部材かどうか確認します。

 

断面係数の不思議（読み飛ばしてもOK）

ところで、一番上の曲げ応力度の式を求める段階で

• Ｍ＝E×I／Ρ

という式が導かれます。

この式は、Ｍの中に断面二次モーメントとヤング係数が関わっています。つまり、部材の「形状」と「材質」ですね。

でも、σ＝Ｍ／Ｚから明らかなように、曲げ応力度は、「曲げモーメントを断面係数で除した値」ですから、部材の「材質」による影響は一切ありません。

部材に作用する応力を「部材の形状に関わる係数」で割ることで得られます。σ（曲げ応力度）は、部材の材質に関わらず求められます。

σ＝Ｍ/Ｚの誘導で部材の「材質」と「形状」が関わる式を使っておきながら、結果として「形状」だけが関係してくる式を導くことが出来たのは不思議ですね。

また、鋼の短期許容応力度ft＝235はσ＝Ｅεという関係から求められます。これは、部材の「材質」と「形状の変化」から応力を求めるフックの法則ですが、σ＝Ｍ／Ｚは「形状」しか関わってきません。それにもかかわらず、得られた曲げ応力度と許容応力度を比較しているのも不思議です。

断面係数　矩形断面公式の導出　もう一つの方法

断面係数の公式は、断面二次モーメントから展開する方法と、もう１つ別の展開があります。これは、部材断面に作用している曲げ応力度の釣り合い式から求める方法です。

まず、矩形断面に曲げ応力が作用している状態を考えます。

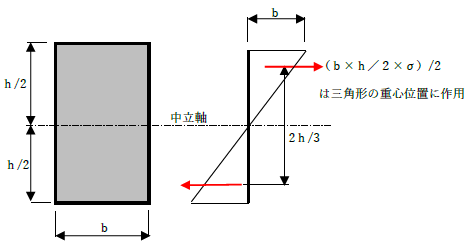
この時、矩形断面ならば中立軸は部材高さの半分です。例えば、高さをｈとするならば（上図の一番上の断面を見てください。）ｈ／２ですね。この中立軸を境に、応力は圧縮・引っ張りに分かれていることを、曲げ応力度の導出でも勉強しました。

曲げ応力は、それぞれ三角形分布のように部材断面に作用しています。少し理解し難いかもしれませんが、圧縮・引張それぞれの曲げ応力を三角形型の分布荷重と考えるなら、三角形の重心位置に集中荷重が作用していると考えることができます。

この時、集中荷重とは三角形の面積×σ（ここでは仮定した値）なので、

• （ｂ×ｈ／２×σ）／2

です。

この応力度を集中荷重に変換した値は、三角形の重心位置に作用しています。また、圧縮・引張りと逆方向に作用している力なので、これは中立軸を基点とした偶力と言えます。つまり、圧縮・引張りそれぞれの重心位置間距離×集中荷重＝偶力ですから、

• （ｂ×ｈ／２×σ）／2×2ｈ／3＝Ｍ

です。σ＝Ｍ/Ｚという関係式を思い出します。すると、式を整理して

• Ｚ＝ｂｈ²／6

が導けました。

実務で使う断面係数

構造設計の実務では、断面係数を暗算で求める場面が多々あります。そのとき使う公式が、

Ｚ＝bh²／6

です。使用例をいくつか紹介します。

ベースプレートのＺを求める

ベースプレートは柱脚を構成する部材の１つです。下図をみてください。これは露出柱脚というごく一般的な柱脚の形状です。

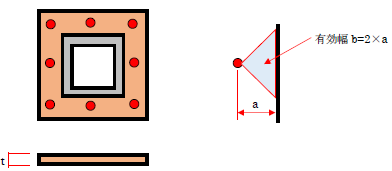
柱脚のアンカーボルトに引張力が作用すると、ベースプレートに曲げモーメントが発生します。この曲げモーメントは、当然ベースプレートで耐える必要があります。つまり、

σ＝Ｍ／Ｚ

を計算して、許容曲げ応力度以下に納まっていればＯＫです。ベースプレートの断面係数は、下式で計算します。

Ｚ＝bt²／6

bは、上図で示す「有効幅」、tはベースプレートの厚みです。

鉄骨階段の蹴上と段板のＺを求める

鉄骨階段はササラ、段板、蹴上で構成されます（蹴上が無い鉄骨階段もあります）。蹴上と段板のある段部は、下図の形状です。

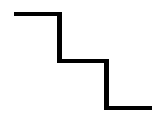
階段は荷重が作用すると曲げモーメントが発生します。この応力は段部で負担しますが、下図の形状の断面係数を考えます。

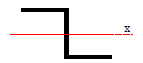
悩みそうな形状ですが実は簡単です。なぜならx軸回り（曲げモーメントが発生する軸回り）の断面係数は、下図と同じだからです。

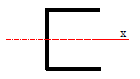
あるいはＨ形鋼の形状とも同じですね。矩形断面ではないので単純にbh2／6で計算するよりも、断面二次モーメントＩを算定し、yoで除して求める方が簡単です。

上図のような中立軸から離れた位置に部材があるときの、断面二次モーメントの求め方は下記の記事が参考になります。

断面二次モーメントとは何か？

まとめ

断面係数とは曲げモーメントに抵抗する値だと覚えてください。また、断面係数はとても重要な値ですが、大本のσ＝Ｍｙ／Ｉが最も重要ですので、まずはここの誘導からできるようになりましょう。※下記の記事が参考になります。

梁の曲げ応力度と誘導方法

断面係数を理解した後は、塑性断面係数と全塑性モーメントに進みましょう。塑性設計に必要な基礎知識です。

塑性断面係数と全塑性モーメント

手前味噌ですが、当HPを１冊の本にしたこちらも参考になります。

わかる構造力学―「数式」や「用語」の意味を「源流」から完全理解! (I・O BOOKS)

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

▼スポンサーリンク▼

【初回資料が今だけ無料！】1日約13円で情報をアップデート！

有料メルマガを無料で見てみませんか？⇒　忙しい社会人、学生のためのビルディング・アップデート

更新情報

• 当サイトでは、ほぼ毎日、記事更新・追加を行っております。


• 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。


• 新着記事一覧

プロフィール

• 
• 略歴▼
• 名前　ハナダユキヒロ/MITUME lab代表.
• 2010年　弊サイトを開設
• 2010～2017年　国立大学大学院修了
• 2017年12月に当HPが書籍化。
• 「わかる構造力学」
• 2022年4月に「わかる構造力学」の改訂版出版。
• 「わかる構造力学(改訂版)」


• 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。


• 当サイトの目的▼
• 建築学生が学ぶ「構造力学」の目的


• とりあえず10記事▼
• 初めましての方に10記事用意しました


• おすすめ書籍紹介▼
• ハナダユキヒロが建築関連書籍の良書を選びました

建築の本、紹介します。▼

▼【好評！】管理人おすすめ▼

• あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！

同じカテゴリの記事一覧

• 断面係数の公式は？1分でわかる求め方、断面二次モーメントとの違い
• 断面係数の単位は？1分でわかる単位、読み方、mmとの関係、断面二次モーメントの単位との違い
• 断面係数を大きくするには？3分でわかる方法、断面係数の大きな形状、断面二次モーメントとの関係
• 断面係数と断面方向の関係は？1分でわかる考え方、求め方、xyの違いは？
• 断面係数と応力の関係は？1分でわかる意味、単位、モーメントとの関係
• 正方形の断面係数は？1分でわかる求め方、中空断面、正方形の断面二次モーメントは？
• 長方形の断面係数は？1分でわかる求め方、長方形の向き、断面二次モーメントとの関係
• 円の断面係数の求め方は？1分でわかる公式、導出方法と計算例