図心ってなに？図心の求め方と断面一次モーメントの関係
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
図心とは何でしょうか。例えば四角形の図心は、明らかに中央にあります。では複雑な形状の図心はどこでしょうか。複雑な図形の図心は、図形の中心にはありません。つまり、
- 図心＝図形の中心
では無いのです。では、図心はどうやって求めるのでしょうか。今回は図心の意味と、図心と中立軸の関係、図心の求め方、図心と断面一次モーメントの関係について説明します。
中立軸、断面一次モーメントの意味、図心と重心の違いは下記が参考になります。
中立軸とは？1分でわかる意味、定義、コンクリートの中立軸、合成梁
図心と重心の違いは？1分でわかる意味、読み方、図心と断面二次モーメントとの関係
図心ってなに？
図心とは、その位置を支点にしたとき、図形が釣り合う点です（ただし重量は均一に作用する）。言葉で説明するより図を見て頂いた方が分かりやすいです。下図を見てください。
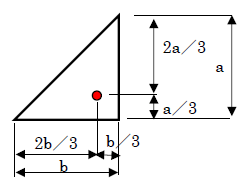
上図のように、直角三角形の重心位置は三角形の長さの1/3にあります。
つまり直角三角形は、上図の赤丸位置を支点にすれば、外部からの影響がない限り、倒れたりしません。下図を見てください。
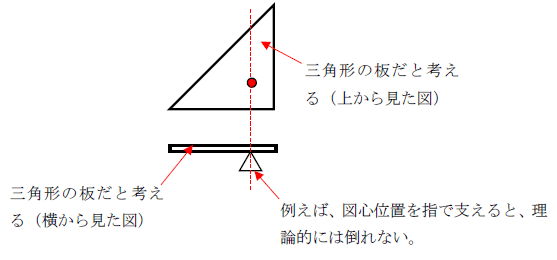
三角形の、木の板があると考えます。前述したように、三角形の図心位置は赤丸印の位置です。この板の図心に指をかざし支えれば、理論上は倒れることはありません。
図心は、図形の形状によって異なります。四角形の図心は、皆さんがご存知の通り中央にありますが、三角形や色々な形によって図心は違うのです。
では、図心はどうやって算定すれば良いのでしょうか。
実は、図心位置を算定するには、ある値を計算する必要があります。それが「断面一次モーメント」です。断面一次モーメントの意味、図心と重心の違いは下記が参考になります。
図心と重心の違いは？1分でわかる意味、読み方、図心と断面二次モーメントとの関係
では、皆さんが断面一次モーメントについて理解頂いたとして、実際に図心を計算しましょう。
100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒ いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事
図心の求め方
さて、図心の求め方は断面一次モーメントを使うことで簡単に求めることができました。会の通りです。
- Σ（A×ｙ）／ΣA
Aは、ある図形の断面積、ｙは、ある図形の図心位置です。つまり、断面積と図心位置までの距離を合計した値を、全断面積で割ればよいのです。
試しに下図の図心位置を求めましょう。
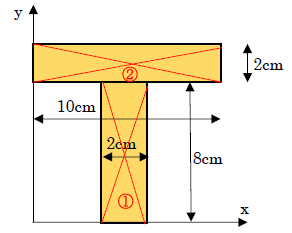
一見、複雑な形をしていて図心位置が難しそうに思います。しかし、実際の計算は簡単です。まず、図心を求める計算式を思い出してください。下記でした。
- Σ（A×ｙ）／ΣA
これは図形を分割して、A×ｙを求め、全断面積で割って求めても良いのです。つまり、上図のように①の図形と、②の図形に分けて考えます。まずｙ方向の図心を求めます。
①の図形は、
A×ｙ＝2×8×4＝64
です。
②の図形は、
A×ｙ＝2×10×9＝180
です。
全断面積は、
A=2×8+2×10＝36
です。
よって、ｙ方向の図心位置は
ｙ＝ (64+180)／36＝6.77⇒6.8ｃｍ
です。
ｘ方向の図心位置も上記と同様の方法で算定できます。但し、今回は左右対称の図形のため、ｘ方向の図心位置は中心です。よって、算定を省略します。
図心と中立軸の関係
部材は曲げモーメントが作用するとき、引張力を圧縮力を受けて曲げられます。部材は中立軸を境に曲げられますが、中立軸では変形していません。
つまり中立軸は応力が作用していない点です。中立軸は部材の図心に等しく、前述した方法により計算します。
中立軸の意味は下記も参考にしてください。
中立軸とは？1分でわかる意味、定義、コンクリートの中立軸、合成梁
まとめ
今回は図心について説明しました。なんとなく図心＝中央と考えがちですが、そうではありません。
図形の形状によって異なる値です。計算方法は、断面一次モーメントが深く関係しています。まだ読んでいない方は、是非読んでみてください。
また、重心の意味、図心と重心の違いも勉強しましょうね。
図心と重心の違いは？1分でわかる意味、読み方、図心と断面二次モーメントとの関係
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
▼スポンサーリンク▼
▼【好評！】管理人おすすめ▼
- あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！
▼用語の意味知らなくて大丈夫？▼
▼同じカテゴリの記事一覧▼
- 断面二次モーメントとは？1分でわかる意味、計算式、h形鋼、公式、たわみとの関係
- 断面二次モーメントの単位は？1分でわかる意味、読み方、換算方法
- 長方形の断面二次モーメントは？1分でわかる求め方と計算式、向きと方向、幅の関係
- 正方形の断面二次モーメントは？1分でわかる公式、計算、断面係数の公式、長方形との違い
- 円の断面二次モーメントの求め方は？1分でわかる公式、導出方法、計算例
- 断面二次モーメントの計算式は？1分でわかる求め方、円、パイプ、i型の計算式
- 断面二次極モーメントとは？1分でわかる意味、長方形の公式と計算方法、単位、断面二次モーメントとの関係
- 断面相乗モーメントとは？1分でわかる意味、公式、計算
- 断面係数とは
- 断面係数の公式は？1分でわかる求め方、断面二次モーメントとの違い
▼カテゴリ一覧▼
- 建築物と構造力学の関係(まずは、苦手な勉強の進め方から)
- モデル化を学ぶ(まずは、構造物のモデル化から)
- 静定構造物の解き方を学ぶ(まずは、静定構造物に関する基礎用語から)
- 断面の性質を学ぶ(まずは、断面図形に関する基礎用語から)
- 梁のたわみを学ぶ(まずは、梁のたわみと基礎用語から)
▼他の勉強がしたい方はこちら▼
【好評】LINEで質問！
管理人に質問してみる？
わかる1級建築士の計算問題解説書
【初回資料が今だけ無料！】1日約13円で情報をアップデート！
有料メルマガを無料で見てみませんか？⇒ 忙しい社会人、学生のためのビルディング・アップデート
わかる2級建築士の計算問題解説書！
【30%OFF】一級建築士対策も◎！構造がわかるお得な用語集
更新情報
- 当サイトでは、ほぼ毎日、記事更新・追加を行っております。
- 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。
- 新着記事一覧
プロフィール
- 略歴▼
- 名前 ハナダユキヒロ/MITUME lab代表.
- 2010年 弊サイトを開設
- 2010～2017年 国立大学大学院修了
- 2017年12月に当HPが書籍化。
- 「わかる構造力学」
- 2022年4月に「わかる構造力学」の改訂版出版。
- 「わかる構造力学(改訂版)」
- 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。
- 当サイトの目的▼
- 建築学生が学ぶ「構造力学」の目的
- とりあえず10記事▼
- 初めましての方に10記事用意しました
- おすすめ書籍紹介▼
- ハナダユキヒロが建築関連書籍の良書を選びました
建築の本、紹介します。▼
▼【好評！】管理人おすすめ▼
- あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！
同じカテゴリの記事一覧
- 断面二次モーメントとは？1分でわかる意味、計算式、h形鋼、公式、たわみとの関係
- 断面二次モーメントの単位は？1分でわかる意味、読み方、換算方法
- 長方形の断面二次モーメントは？1分でわかる求め方と計算式、向きと方向、幅の関係
- 正方形の断面二次モーメントは？1分でわかる公式、計算、断面係数の公式、長方形との違い
- 円の断面二次モーメントの求め方は？1分でわかる公式、導出方法、計算例
- 断面二次モーメントの計算式は？1分でわかる求め方、円、パイプ、i型の計算式
- 断面二次極モーメントとは？1分でわかる意味、長方形の公式と計算方法、単位、断面二次モーメントとの関係
- 断面相乗モーメントとは？1分でわかる意味、公式、計算
- 断面係数とは
- 断面係数の公式は？1分でわかる求め方、断面二次モーメントとの違い
- HOME > 構造力学の基礎 > 図心ってなに？図心の求め方と断面一次モーメントの関係
- 1級の過去問(計算)解説
- 限定メルマガ
- わかる建築構造の用語集・図解集
- 1頁10円！PDF版の学習記事