建築学生が学ぶ構造力学

【好評】LINEで質問 構造力学が苦手 おすすめ書籍 おすすめPDF教材 無料メルマガ 図解集 用語集
  1. HOME > 構造力学の基礎 > ヤング係数とは？求め方と公式、単位、材料ごとの値【図解】

ヤング係数とは？求め方と公式、単位、材料ごとの値【図解】

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

ヤング係数


ヤング係数は「材料のもつ固有のかたさ（変形のしにくさ）を表す値」です。


つまり、ヤング係数の大きい材料ほど「変形は小さく」なります。

ヤング係数の意味

言ってしまえば、その一言でヤング係数の解説は済みますが、それだけでは「ヤング係数を適切に理解している」とは言えません。意外と奥が深いのです。


今回は「ヤング係数ってなに？」という疑問に建築構造の専門家がわかりやすく、徹底的に解説します。

ヤング係数は材料のかたさ（変形のしにくさ）

さて、ヤング係数は"材料固有のかたさ"（※言い換えるなら、変形のしにくさ）で、下記のことが言えます。


１．"材料ごと"にヤング係数の値は違う

２．部材形状や部材の断面形状を変化させても"ヤング係数は変わらない"

３．ヤング係数が大きいほど変形しにくい


それぞれ解説します。ヤング係数は材料のもつ「固有のかたさ」を表す値です。


言い換えれば「材料ごとにヤング係数（かたさ）は異なる」という意味です。


石と糸では全く固さが違うことをイメージすれば良いでしょう。


また、鋼、木のように、材料のかたさが違うことも、日常生活で身に付けた直観力から理解頂けるはずです。

ヤング係数は材料ごとに違う

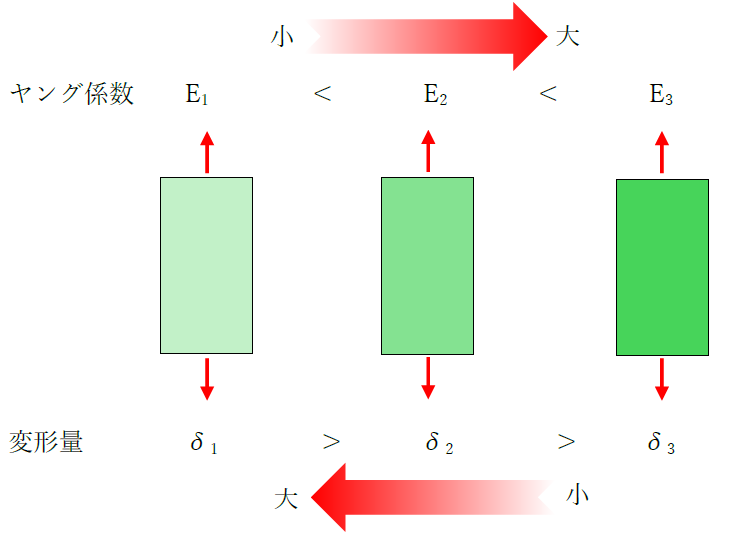
「ヤング係数≒材料のかたさ」ですから、同じ力で異なる材料（材料の断面形状は同じとする）を引張ると、


その変形量は「ヤング係数の大きさに反比例」します。


つまり、ヤング係数が大きいほど「かたい材料」なので、変形量は小さくなります。


逆にヤング係数が小さければ、部材は柔らかくなります。

ヤング係数が大きいほど変形しにくい

部材の変形量を小さくしたければ「ヤング係数の大きい材料を用いる」ことも方法の１つです。


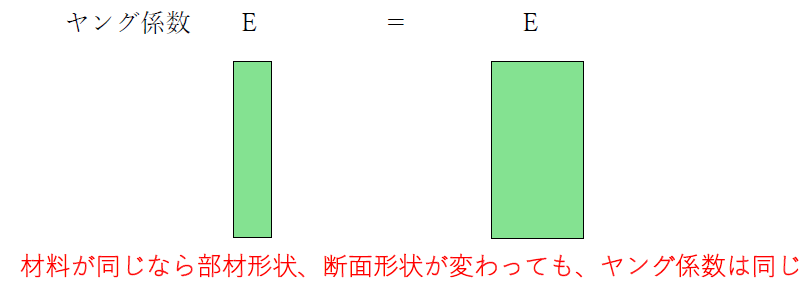
また、ヤング係数は材料のもつかたさなので、部材形状や部材の断面形状をかえても「ヤング係数自体が変わるわけでは無い」です。


石を磨いてキラキラにしても金や銀にはならず"石のまま"ということです。

ヤング係数は材料のもつかたさ

ただし、部材のかたさはヤング係数だけでなく、他２つの要素で決定します。１つは「部材の断面形状」、2つめが「部材の長さ」です。


つまり、ヤング係数を加えて合計３つの要素から部材のかたさは決まります。何が言いたいかというと


・部材のかたさは、必ずしもヤング係数の大小だけで決まるとは限らない


ことです。仮にヤング係数の大きな材料を用いても、断面形状や部材長さによっては「変形しやすい部材となる」ことも多いので注意しましょう。


断面形状のもつかたさを表す値を「断面二次モーメント」といいます。断面二次モーメントの詳細は下記をご覧ください。

断面二次モーメントとは？1分でわかる意味、計算式、h形鋼、公式、たわみとの関係

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

記事を書いた人

ハナダユキヒロ／建築学生が学ぶ「構造力学」

難解な構造力学、建築構造の用語を分かりやすく解説する専門家。高等専門学校在学中から建築学生が学ぶ「構造力学」を運営。その後、国立大学大学院⇒組織設計事務所⇒弊サイト運営に従事している。

著書：「わかる構造力学/工学社」、「わかる構造力学 改訂版/工学社」

LINEで質問したい方はこちら　⇒　【好評】管理人にLINEで質問してみよう

ヤング係数の求め方と公式

ヤング係数の求め方は、ヤング係数の力学的な意味を踏まえて理解しましょう。ポイントは下記の２つです。


１．ヤング係数は、応力度とひずみの比例定数である（フックの法則に従う）

２．上記は材料が弾性範囲の場合のみ成立する


はじめにヤング係数の求め方の公式を示します。Eはヤング係数、σは応力度（σ＝P/A）、εをひずみ（ε＝ΔL/L）といいます。下式を変形すると「σ＝Eε」となり本式をフックの法則といいます。

E=σ/ε

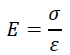
フックの法則は材料の弾性範囲において「力と変形が比例関係」にあることを示す法則です。


σ=Eεは切片が0の一次関数（y=ax）なので、ヤング係数とは「σはεに比例するときの比例定数」といえます。※どのように本式（フックの法則）が導かれたかは後述します。


また、y=axのaは一次関数の傾きであることと同様に、応力度σを縦軸、ひずみεを横軸にとったグラフ（応力ひずみ曲線）を描いたときの「傾きがヤング係数に等しい」のです。

ヤング係数の求め方

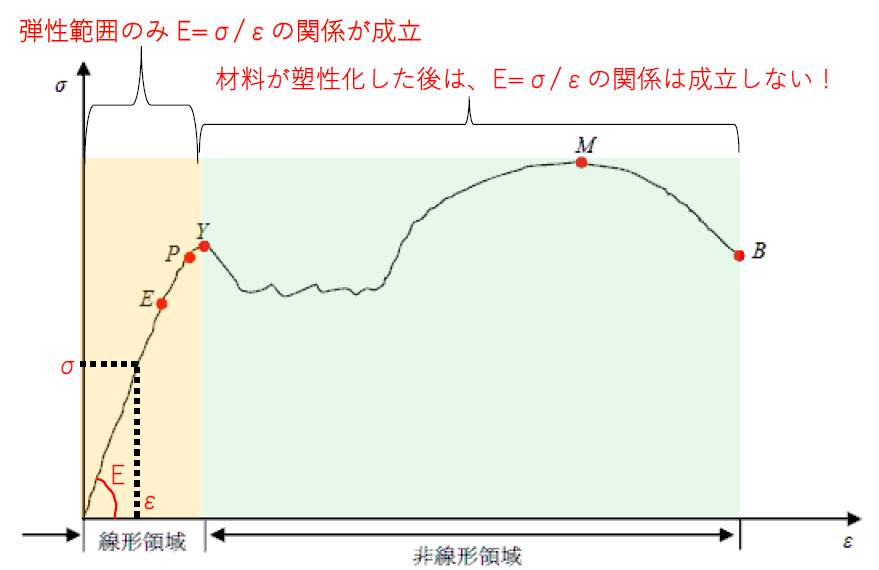
ただしフックの法則は、応力度σとひずみεが比例関係（y=ax）にあることが前提となります。


言い換えるなら、応力度σとひずみεの関係が"弾性範囲"の場合のみ本関係は成立します。


よって、ヤング係数を「弾性係数」ともいいます。これは文字通り「弾性範囲内で成り立つ係数であること」を意味します。


さて、上図のようにσを縦軸、εを横軸にとったグラフを「応力ひずみ曲線」といいます。なお上図は鋼材の応力ひずみ曲線を表しており、点Yを降伏点といいます。


鋼材は、弾性（力を加えると変形するが、力を取り除くと変形も無くなり元の状態に戻る性質）を持っていますが、


力を加えすぎると塑性化（力を取り除いても変形が残る状態になったこと）します。


鋼材の場合、弾性範囲ではy=axの関係が成立しますが、材料が塑性化して以降はy=axの関係が成立しませんので、


ヤング係数は「あくまでも材料の弾性範囲内における"かたさ"」を意味します。


また、鋼材の弾性範囲内においては「応力度とひずみの関係は線形（直線的）である」ため「σ＝Ｅε　⇒　Ｅ＝σ/ε」の関係がピタリと当てはまります。


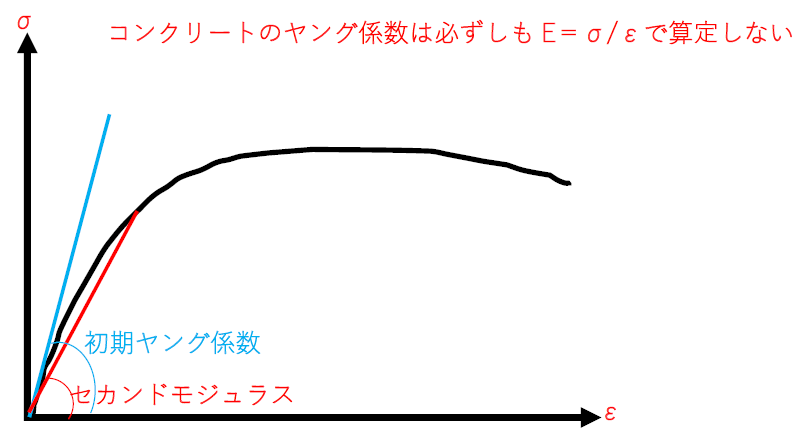
一方で、ネットの記事では誤った解説も多いので注意して頂きたいですが、弾性範囲だとしてもコンクリートは応力度σとひずみεの関係は「必ずしも線形ではなく曲線」となります。


つまり、コンクリートの場合、σとεのとる位置によってEは変化しますので、単純にE=σ/εに当てはめてもダメで、そのため、ヤング係数を求める様々な推定式が提案されています。

コンクリートのヤング係数

以上より、ヤング係数の求め方も「実は材料により違う」ので注意しましょう。

ヤング係数Eとσ＝Eεの導き方

フックの法則は、物体の弾性を示した人物ロバート・フック(1635-1703)により実験的に示されました。


下図をみてください。バネに重りを付けると重りの質量分、バネは変形します（伸びる）。フックの実験は、バネに付けた重りの質量と、重りに応じた変形量を測定して関係性を導いたことです。

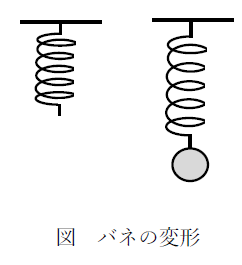
フックの法則

本実験により、力と変形は比例関係にありこれをフックの法則といいます。力が作用すると変形し、力を取り除くと変形は0になるのですから、力と変形の関係は下式で示されます。

f=kx

fは力、kはバネのかたさ（剛性またはバネ定数という）、xは変形量です。なお、kの単位は単位長さ当たりの力でN/cm、kN/cmなどを用います。


上式よりkが大きいほど変形量x小さくなります。つまり、バネがかたくなるほどバネの伸びは小さいことを意味し、これは直感的にも理解できます。


fを縦軸、xを横軸にすると下図のような1次関数が描けます。この直線の傾きがkとなり、kは一定の値ですから、力の大きさ又は変形の大きさの一方が既知であれば、他方を算定できます。

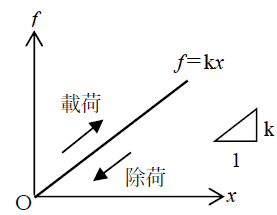
フックの法則

フックの法則f=kxは、変位量xと力fが比例関係にあることを示しますが、部材のかたさを表すkは同じ材料を用いても断面の形状や大きさ部材の長さが影響するため、やや扱いづらさが残ります。


そこでフックの法則の力を応力度σに、変位量をひずみεに置き換えるとき、バネ定数kはヤング係数Eと定義されて下式のように示されます。

σ=Eε

Eはトーマス・ヤング（1773-1829）によって取り入れられたことからヤング係数（ヤング率、弾性係数）と言います。

ヤング係数の値と材料の関係

建築物に用いる構造材料のヤング係数を下表に示します。下表の通り、ヤング係数は各材料により値が異なります。また、コンクリートのように計算式により算定する場合もあります。


表　各材料のヤング係数

材料 ヤング係数
鋼材 205000
コンクリート 3.35 × 104 × ( γ / 24 )2 × ( Fc / 60 )1/3
木 7000～12000
アルミ 7000(鋼の1/3程度)

鋼やアルミは強度がいくら高くても、ヤング係数は一定です。一方、コンクリートは強度が高くなるほどヤング係数も高くなります。


近年は、高強度コンクリートの研究が行われており、圧縮強度が鋼に迫る勢いです。その分ヤング係数も高くなるので、鋼よりも優れた材料になるかもしれません。


木は、スギやヒノキなど種類によって強度もヤング係数も違います。木は生き物ですから、鋼やコンクリートよりも扱いにくいと覚えてください。


それでは各材料のヤング係数について解説します。

鋼のヤング係数

鋼のヤング係数は205000N/mm2です。前述したように、鋼は弾性範囲では概ねσとεは比例関係にあります。


よって、鋼の弾性範囲内において任意のε、それに応じたσについて「E＝σ/ε」を計算すれば「鋼のヤング係数E＝205000N/mm2」が得られます。

鋼のヤング係数

鋼材のヤング係数は？1分でわかる値、Mpa、kN/㎡の値、ss400との関係

コンクリートのヤング係数

コンクリートのヤング係数はσとεの関係が比例ではありません。

コンクリートのヤング係数

上図のように、応力度とひずみの関係の初期のヤング係数と、ひずみが進行してからのσとεの関係によるヤング係数（セカンドモジュラス）では、値が変わります。


要するに、コンクリートは鋼のようにヤング係数は一定では無いため、様々な推定式が提案されています。現在、コンクリートのヤング係数は下式より算定します。

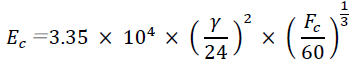
E_c＝3.35 × 10^4 × ( γ/24 )^2 × ( F_c/60 )^(1/3)

Ecはコンクリートのヤング係数、γはコンクリートの単位体積重量、Fcはコンクリートの設計基準強度です。例題としてFc=24、γ=23の普通コンクリートのヤング係数を求めると。

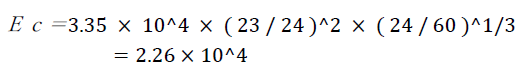
Ｅｃ＝3.35 × 10^4 × ( 23 / 24 )^2 × ( 24 / 60 )^1/3=2.26×10^4

になります。コンクリートの比重や、設計基準強度Fcについては、下記が参考になります。

コンクリートの比重は？鉄筋コンクリートとの違い、骨材、鉄筋の影響

設計基準強度と品質基準強度の違いと、５分で分かるそれぞれの意味

木材のヤング係数

木はその種類に応じてヤング係数も変わります。また、木の場合、木の繊維方向と繊維直交方向ではヤング係数が変わる点に注意が必要です。

まとめ

今回はヤング係数について説明しました。ヤング係数の意味、各材料のヤング係数など覚えておきましょう。鋼のヤング係数は良く使うので、値を暗記しておくと便利ですよ。下記も併せて参考にしてください。

ヤング率が大きいとは？1分でわかる意味、かたさとの関係、ヤング率の大きい（高い）材料

ヤング率とポアソン比の関係は？1分でわかる意味と違い、求め方

ヤング率の単位は？1分でわかる単位、意味、読み方、MPa、kgf/mm2との関係

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）


▼スポンサーリンク▼

▼【好評！】管理人おすすめ▼

▼用語の意味知らなくて大丈夫？▼

建築学生が学ぶ「構造力学」の用語集

▼同じカテゴリの記事一覧▼

▼カテゴリ一覧▼

▼他の勉強がしたい方はこちら▼

建築構造がわかる基礎図解集

noteで学ぶ建築士試験の構造

ゼロから建築士試験の構造を勉強しよう～！

ゼロから学ぶ建築士試験の構造

【好評】LINEで質問！

管理人に質問してみる？

友だち追加

わかる1級建築士の計算問題解説書

計算の流れ、解き方がわかる！1級建築士【構造】計算問題解説集

【初回資料が今だけ無料！】1日約13円で情報をアップデート！

有料メルマガを無料で見てみませんか？⇒　忙しい社会人、学生のためのビルディング・アップデート

わかる2級建築士の計算問題解説書！

【30%OFF】一級建築士対策も◎！構造がわかるお得な用語集

建築学生が学ぶ「構造力学」の用語集
pdf版の学習記事

更新情報

プロフィール

建築の本、紹介します。▼

すぐにわかる構造力学の本

▼【好評！】管理人おすすめ▼

同じカテゴリの記事一覧

Topへ >>

  1. HOME > 構造力学の基礎 > ヤング係数とは？求め方と公式、単位、材料ごとの値【図解】
  2. 1級の過去問(計算)解説
  3. 限定メルマガ
  4. わかる建築構造の用語集・図解集
  5. 1頁10円！PDF版の学習記事