1. HOME > 構造力学の基礎 > 剛性とは？簡単な意味、剛性の計算、単位、強度との違い

剛性とは？簡単な意味、剛性の計算、単位、強度との違い

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

剛性の意味をご存じでしょうか。剛性は、物体の変形のしにくさ（しやすさ）を表す値です。建築では、地震などの力に対して剛性の大きさが重要です。また、建築以外でも（例えば自動車）剛性は大切です（自動車なら、衝撃による変形量を推定するなど）。

今回は、そんな剛性に着目し、意味、剛性とヤング率との関係、強度との違い、単位などあらゆる側面から剛性について説明します。

似た用語に、剛比があります。剛比の意味は、下記が参考になります。

剛比とは？3分でわかる剛比の意味と計算方法

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

記事を書いた人

ハナダユキヒロ／建築学生が学ぶ「構造力学」

難解な構造力学、建築構造の用語を分かりやすく解説する専門家。高等専門学校在学中から建築学生が学ぶ「構造力学」を運営。その後、国立大学大学院⇒組織設計事務所⇒弊サイト運営に従事している。

著書：「わかる構造力学/工学社」、「わかる構造力学 改訂版/工学社」

LINEで質問したい方はこちら　⇒　【好評】管理人にLINEで質問してみよう

剛性とは？

剛性は、物体の固さ（かたさ）を表す値です。要するに、剛性の大小が「固い」「柔らかい」を意味します。剛性を説明するとき、「ばね」を使います。ばね、は私達の生活に身近な道具です。ボールペンを分解すると、ばねがでてきます。

ばねは押さえつけると変形しますが、力を抜くと元に戻ります。この性質を「弾性」といいます。弾性については下記が参考になります。

塑性とは？1分でわかる意味、靭性、延性、弾性との違い、対義語、塑性変形能力との関係

ばねの中には「固いばね」と「柔らかいばね」があります。固いばねは、中々変形しません。一方柔らかいばねは、手で簡単に変形します。剛性は、このような固さ（すなわち変形のしやすさ）を表しています。

では、剛性の意味が分かったところで、実際に剛性の計算をしてみましょう。剛性が大きければ、変形しにくい部材です（つまり固い）。逆に剛性が小さければ変形しやすいです（柔らかい）。剛性をk、変形をδとします。このとき剛性と変形の間には、下式が成り立ちます。

P＝kδ

よって、剛性kは下式で計算します。

k＝P／δ

Pは荷重（単位はN、kNなど）、kは剛性（N/mm、kN／cmなど）、δは変形（mm、mなど）です。これを「フックの法則」といいます。物理学者ロバートフックは、バネ秤を用いた実験で、力と変形は比例関係にあることを見つけました。

また、バネの固さによって変形量が違うことにも気づいたのです。バネの固さとは、つまり「剛性の大きさ」です。

上式は、定量的な分析（量に着目すること。上式なら荷重の量や、変形量）には役立ちますが、物体を定性的に分析できません（本質的な性質）。そこで上式を下記のように変形します。当式もフックの法則と言います（こちらが有名かもしれません）。

σ＝Eε

σは応力度（曲げ応力度又は軸応力度）、Eはヤング係数、εはひずみ（ひずみ度）です。※ヤング係数については下記が参考になります。

ヤング係数ってなに？1分でわかるたった1つのポイント

剛性の意味は前述した「変形のしにくさを示す値」で間違いないのですが、「変形」にも色々あります。部材を単純に引っ張ったときの変形と、曲げた時の変形は違うはずです。それは、「剛性の違い」でもあります。

建築では主に３つの変形を考えます（今回、ねじれの話は省略します）。

・軸変形

・曲げ変形

・せん断変形

軸変形による剛性を「軸剛性」といいます。また曲げ変形、せん断変形による剛性を、それぞれ「曲げ剛性」「せん断剛性」といいます。

単に「剛性」といっても、実は３種類あることを覚えておきましょう。ですから「剛性」という用語は曖昧な言い方です。前述したように、「一体どのような変形に対する剛性なのか」は大切だからです。

剛性と強度の違い

剛性と強度を混同する理由は２つあります。

１．強度の正しい意味を認識していない

２．強度＝固いという誤った認識

「強度が高い」というと、何となく「固い」と連想しがちです。しかし、強度と剛性は全く関係しません。一番良い例は「糸」です。糸の強度は驚くほど高いです。一方で糸は、柔らかい材料ですよね。強度と剛性が全く結びついていない証拠です。

剛性の意味は前述しました。固さを表す値です。強度とは、「材料が、どのくらいの単位面積当たりの力に耐えられるか」示す値です。建築で単に「強度」というと、材料強度や許容応力度など様々な強度があります。剛性と同じく、曖昧な用語です。

※材料強度や、許容応力度については下記が参考になります。

材料強度がわかるたった2つのポイントと、許容応力度の関係

許容応力度計算が簡単にわかる、たった３つのポイント

剛性と変形の関係

さて、剛性は３種類あると説明しました。各剛性は変形と関連づけると理解しやすいです。各剛性について計算式や特徴を説明します。

軸剛性と軸変形

軸変形とは、下図のように部材に引張力又は圧縮力のみ作用するときの変形です。

軸剛性の計算式を導出します。

P＝kδ

σ＝P／A

σ＝Eε

ε＝ΔL／L

以上の式を紐づけて、kを求める形に直します。

P／A＝Eε

P／A＝E*ΔL／L

P＝E*ΔL*A／L

ΔL＝δより

P＝δ*EA／L

P＝kδの式と上式を紐づけます。よってkは、

k ＝EA／L

です。kは軸剛性、Eはヤング係数、Aは部材の断面積、Lはスパンです。軸剛性は、ヤング係数と断面積の積に比例し、スパンに反比例します。

曲げ剛性と曲げ変形

部材を曲げると、曲げ応力（曲げモーメント）が作用します。また、この時部材は曲げ変形を伴います。曲げ変形は「梁のたわみ」と言った方が分かりやすいでしょうか。例えば、下図の単純梁に集中荷重が作用しています。梁のたわみは、PL3／48 EIです。

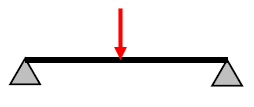
フックの法則より

P＝kδ

δ＝PL3／48 EI

です。よって曲げ剛性kは、

k＝P／δ＝P／（PL3／48 EI）＝48EI／L3

です。曲げ剛性の大きさは、ヤング係数Eと断面二次モーメントIの積に比例し、スパンLの三乗に反比例します。

曲げ変形に強い（たわみにくい）部材とは、ヤング係数、断面二次モーメントが大きい部材です。

※ヤング係数、曲げ剛性については下記が参考になります。

ヤング係数ってなに？1分でわかるたった1つのポイント

曲げ剛性の基礎知識、1分でわかる意味と計算方法

せん断剛性とせん断変形

せん断力が作用すると、物体は下図のように変形します。このような変形をせん断変形と言います。

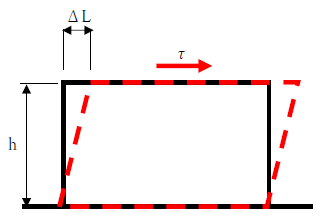
せん断力とせん断変形の間にも、フックの法則が成り立ちます。但しせん断力に対しては別途フックの法則が成り立ちます。下式をみてください。

τ＝Ｇγ

τはせん断応力度、Ｇはせん断弾性係数、γはせん断変形です。※せん断弾性係数については下記が参考になります。

横弾性係数の基礎知識と、縦弾性係数との関係

またせん断応力度は、下式でも計算できます。

τ＝Q／A

τはせん断応力度、Qはせん断力、Aは断面積です。※ところで、曲げモーメントが作用する梁のせん断応力度については下記が参考になります。

梁のせん断応力度

２つの式を紐づけて、剛性の形に直します。

Q／A＝Ｇγ

Q＝ＧγA

＝ＧAΔL/L

よってせん断剛性は、

k＝ＧA/L

下記も参考にしてくださいね。

せん断剛性とは？1分でわかる意味、計算、単位、ヤング率、曲げ剛性との関係

剛性の単位

以上、各変形による剛性を計算しました。計算式から明らかなように、剛性の単位は

N／mm又はkN／cm

などです。後述するバネ定数も、同様の値です。下記も参考にしてください。

曲げ剛性の単位は？1分でわかる意味、軸剛性との違い、梁、eiとの関係

剛性とばね定数の違い

剛性とばね定数は同じ意味と考えてください。物理用語としては「ばね定数」、建築や工学分野では「剛性」という程度の違いでしょうか。実質は同じです。ばね定数の単位が、

N／mm又はkN／cm

な点からも明らかです。但し、後述する柱脚の剛性は、なぜか「ばね定数」という方もいます。又は回転剛性ともいいます。ばね定数の詳細は下記もご覧ください。

ばね定数とは？1分でわかる意味、公式、ヤング率、単位、求め方

柱脚のバネ定数（回転剛性）の求め方

柱脚のバネ定数は下式で計算します。

Kbs＝(E*nt*Ab*(dt+dc)^2)／2*Lb

Kbsがばね定数、Eはヤング係数、ntは引張側のアンカーボルト、Abはアンカーボルトの軸断面積、dtは柱芯からアンカーボルト芯までの距離、dcは柱芯から柱面までの距離、Lbはアンカーボルトの有効長さです。

Abは有効断面積ではなく軸断面積です。また切削ネジと転造ネジの違いで、軸断面積が異なるので注意しましょう。

演習　片持ち柱の曲げ剛性の計算

下図の片持ち柱に集中荷重が作用しています。この部材の曲げ剛性を計算してください。

前述した例を思い出せば簡単ですね。片持ち柱の変形は下式です。

δ＝PL3／3EI

フックの法則より、剛性kは

k＝3EI／L3

です。

補足　剛性と剛度、剛比の関係

剛性は、地震力の計算で大切です。なぜなら、各柱が負担する地震力は剛性の大きさに応じて変わるからです。

前述したように剛性は、スパン、断面二次モーメント、ヤング係数によって決まります。ヤング係数は、各部材で同じはずなので問題になりません。しかし柱や梁の断面は、全て同じではなく意匠・構造・設備設計の兼ね合いで変わります。

剛比とは、各部材による剛性の大きさを比率によって表した値です。剛比は、Ｄ値法や固定モーメント法などの応力算定に用いられます。剛度は、

K＝I／L

で求まる値で、剛比の算定に使います。

※剛比の計算方法については、下記が参考になります。

剛比とは？3分でわかる剛比の意味と計算方法

まとめ

今回は、剛性について説明しました。剛性が実に幅広い意味を含んでいると気づいたでしょう。剛性＝固さ、で間違いないのですが部材には様々な変形があるので、剛性の計算方法も変わります。余裕がある人は、剛比の考え方も理解したいですね。剛比の計算が、構造計算の基本になります。下記も併せて学習しましょう。

曲げ剛性の単位は？1分でわかる意味、軸剛性との違い、梁、eiとの関係

強度と剛性の違いは？1分でわかる違い、相関、靭性との関係

せん断剛性とは？1分でわかる意味、計算、単位、ヤング率、曲げ剛性との関係

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

▼スポンサーリンク▼

【初回資料が今だけ無料！】1日約13円で情報をアップデート！

有料メルマガを無料で見てみませんか？⇒　忙しい社会人、学生のためのビルディング・アップデート

更新情報

• 当サイトでは、ほぼ毎日、記事更新・追加を行っております。


• 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。


• 新着記事一覧

プロフィール

• 
• 略歴▼
• 名前　ハナダユキヒロ/MITUME lab代表.
• 2010年　弊サイトを開設
• 2010～2017年　国立大学大学院修了
• 2017年12月に当HPが書籍化。
• 「わかる構造力学」
• 2022年4月に「わかる構造力学」の改訂版出版。
• 「わかる構造力学(改訂版)」


• 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。


• 当サイトの目的▼
• 建築学生が学ぶ「構造力学」の目的


• とりあえず10記事▼
• 初めましての方に10記事用意しました


• おすすめ書籍紹介▼
• ハナダユキヒロが建築関連書籍の良書を選びました

建築の本、紹介します。▼

▼【好評！】管理人おすすめ▼

• あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！

同じカテゴリの記事一覧

• 曲げ剛性の基礎知識、1分でわかる意味と計算方法
• 曲げ剛性の単位は？1分でわかる意味、軸剛性との違い、梁、eiとの関係
• 強度と剛性の違いは？1分でわかる違い、相関、靭性との関係
• せん断剛性とは？1分でわかる意味、計算、単位、ヤング率、曲げ剛性との関係
• ヤング係数ってなに？1分でわかるたった1つのポイント
• ヤング率が大きいとは？1分でわかる意味、かたさとの関係、ヤング率の大きい（高い）材料
• ヤング率の公式は？1分でわかる求め方、単位、公式と伸びの関係
• ヤング係数の求め方は？1分でわかる求め方、コンクリート、鋼材の値、グラフの傾きとの関係
• 横弾性係数の基礎知識と、縦弾性係数との関係
• 横弾性係数の一覧は？3分でわかる値、単位、縦弾性係数との違い
• 弾塑性とは？1分でわかる意味、読み方、材料、弾性と塑性の違い