- 【無料お試しキャンペーン中！】1級・2級建築士試験の構造の疑問を気軽に相談 初心者でもわかる！1級・2級建築士試験(構造)相談カフェ
- 管理人が業界分析！1日13円で建築業界がわかるLINE配信！ ⇒ まずはリンクをクリックして友だち追加！
面積と積分の関係は？1分でわかる意味、公式、なぜ積分で面積を計算するのか
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
ある線分を積分すると、面積になります。また、任意な形状の微小面積を積分すると、任意断面の面積になります。今回は、面積と積分の関係、積分の公式、なぜ積分で面積が計算できるのか、わかりやすく説明します。なお、数学的な説明ではなく、建築の実務を元に、算数程度の知識で積分を体験しましょう。
100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒ いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事
面積と積分の関係は？
積分は、ある線分、微小面積などの「総和」を意味します（※数学的な意味では無いです）。総和とは、「合計」のことです。下図をみてください。四角形（図形Ａ）があります。
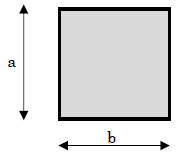
私たちは、四角形の面積の公式が、
- 面積＝a×b
だと知っています。では、別の方法で四角形（図形Ａ）の面積を算定できないでしょうか。その答えが「積分」です。積分とは、「総和（合計）」を意味しました。微小な面積を少しずつ合計（積分）し、求めたかった形状の面積を算定します。
下図のように、まず単位幅当りで長さaの微小面積を計算します。微小面積の大きさは下記です。
- 微小面積＝１×a＝a
単位幅当りなので、1をかけるだけですね。
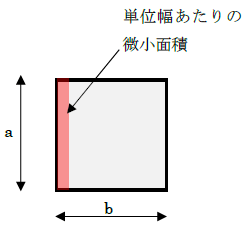
微小面積は、単位幅当りの値です。これを、「ｂ」という長さに渡って合計すれば、長さa×bの面積が算定できます。微小面積をｂという長さ分、積分すれば、
- a×（1+1+・・・・＝b）＝a×ｂ
です。※（1+1+・・・・＝b）とは、単位幅をｂになるまで加えることを意味します。
上記より、積分で四角形の面積を計算しました。「微小面積を合計する」ことが、積分の本質的な意味です（微小体積を合計すれば、体積が算定できます）。
なお、数学的には「∫（いんてぐらる）」を使い、積分を行います（∫は積分記号です）。
積分の公式
積分の公式は下記です。
- A＝∫dA
Ａは任意断面の面積、∫は積分記号です。∫に下添え字、上添え字をつけて、積分する範囲を指定できます。dAは微小面積の意味です。
例えば∫に「下添え字0、上添え字10」という数値が付きました。微小面積dAは、0～10の範囲まで積分を行う、という意味です。
なぜ積分で面積を計算するのか？
積分を使って面積の求め方を説明しました。例題にした「四角形の面積」では、積分のメリットを感じられなかったと思います。
積分を使った面積の算定で、最大のメリットは、
任意断面の面積が計算できる
ことです。下図をみてください。任意断面の面積は計算が困難です。公式もありません。しかし、四角形の微小面積dAを合計すれば、どうでしょうか。dAを、任意断面を埋め尽くすように合計すれば、面積が算定できます。
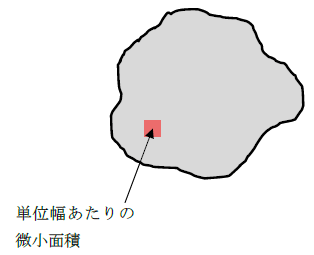
よって、微小面積dAは細かい値でないと意味がないです。下図のように、dAが大きいと、任意形状の断面ができないからです。
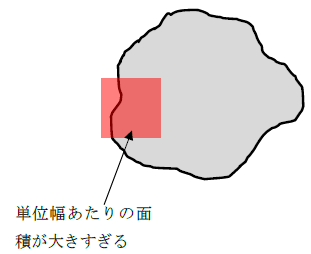
まとめ
今回は面積と積分の関係について説明しました。意味が理解頂けたと思います。積分と聞くと、「∫（いんてぐらる）」のような難しい記号を思い浮かべます。数学的にはそうですが、本質的な意味は簡単です。建築の実務では、積分を使う機会があります。ぜひ、積分の本質的な意味を理解してくださいね。
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
▼人気の記事ベスト３▼
- 1.断面係数の計算方法を本当にわかっていますか？→断面係数とは？
- 2.丸暗記で良いと思ったら大間違い→断面二次モーメントとは何か？
- 3.違いを適切に説明できますか？→等分布荷重とは？集中荷重との違いや使い方について
▼用語の意味知らなくて大丈夫？▼
▼同じカテゴリの記事一覧▼
- 建築学生のメモ
- 建築学科の大学ランキングと進学後の就職について
- 構造設計者に成るための就職先について
- どうすれば構造設計者になれる？ 実務経験と資格について
- 工学系大学を卒業した社会人が、ものづくりが嫌いだと気づいたとき読む記事
▼カテゴリ一覧▼
▼他の勉強がしたい方はこちら▼
【読まれています】管理人による建築業界の分析！
1日13円で建築業界がわかるLINE配信！。
わかる1級建築士の計算問題解説書
あなたは数学が苦手ですか？
【有料メルマガの初回資料が今だけ無料！】1日約13円で情報をアップデート！
有料メルマガを無料で見てみませんか？⇒ 忙しい社会人、学生のためのビルディング・アップデート
わかる2級建築士の計算問題解説書！
【30%OFF】一級建築士対策も◎！構造がわかるお得な用語集
更新情報
- 当サイトでは、ほぼ毎日、記事更新・追加を行っております。
- 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。
- 新着記事一覧
プロフィール
- 略歴▼
- 名前 ハナダユキヒロ/MITUME lab主宰.（筆者のコラムはこちら）
- 2010年 弊サイトを開設
- 2010～2017年 国立大学大学院修了
- 2017年12月に当HPが書籍化。
- 「わかる構造力学」
- 2022年4月に「わかる構造力学」の改訂版出版。
- 「わかる構造力学(改訂版)」
- 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。
- 自己紹介▼
- 建築学生が学ぶ「構造力学」とは？
- とりあえず10記事▼
- 初めましての方に10記事用意しました
- おすすめ書籍紹介▼
- ハナダユキヒロが建築関連書籍の良書を選びました
建築の本、紹介します。▼
同じカテゴリの記事一覧
- HOME > 構造力学の基礎> 面積と積分の関係は？1分でわかる意味、公式、なぜ積分で面積を計算するのか
- 1級の過去問(計算)解説
- 限定メルマガ
- わかる建築構造の用語集・図解集
- 1頁10円！PDF版の学習記事