1. HOME > 構造力学の基礎 > 力のモーメントってなに？本当にわかるモーメントの意味と計算方法

力のモーメントってなに？本当にわかるモーメントの意味と計算方法

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

力のモーメント（モーメント）とは何でしょうか。もしかすると、書籍やネットの記事を色々読んでもピンと来なかった人が多いかと思います。その理由は、教科書的な説明ばかりで、

「力のモーメント」が私達の生活や実現象に、どう結びついているのか見えないからです。

私は建物の構造設計に携わっています。毎日のように、力のモーメントを計算し、力のモーメントに対して建物が安全であるよう検証してきました。それらは空想上の話ではなく、力のモーメントを実際の現象として捉えているのです。

今回はその経験を元に、力のモーメントが何か説明すること、また実際問題、力のモーメントは私たちの生活とどのように関係するのか説明します。

構造力学で最も重要な法則の１つに、「モーメントのつりあい」があります。詳細は下記をご覧ください。

モーメントのつり合いとは？1分でわかる意味、考え方、重心位置の求め方は？

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

記事を書いた人

ハナダユキヒロ／建築学生が学ぶ「構造力学」

難解な構造力学、建築構造の用語を分かりやすく解説する専門家。高等専門学校在学中から建築学生が学ぶ「構造力学」を運営。その後、国立大学大学院⇒組織設計事務所⇒弊サイト運営に従事している。

著書：「わかる構造力学/工学社」、「わかる構造力学 改訂版/工学社」

LINEで質問したい方はこちら　⇒　【好評】管理人にLINEで質問してみよう

力のモーメントってなに？

初めに、一般的になされる力のモーメントの説明をしておきます。下図をみてください。色々な記事で散見されますね。

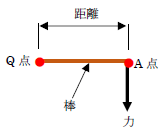
「Q点を固定して、Ａ点から力を加えると棒は回転する。この棒を回転させる力の大きさが、力のモーメントだ」と説明されます。それ自体間違いではありません。

一応計算式で示すと、力のモーメントは

｢作用させる力×Q点からA点までの距離｣

です。

上記の説明で「理解した」と思っている方、「理解できない」方、実際に上図の状況を想像できますか？私はできません。そもそもQ点は固定しているのに回転するなんて、どういう状況でしょうか？「棒を固定するのに、回転するなんて矛盾していないか」と思う方が普通です。この力のモーメント以前の、説明文の矛盾が理解を遅らせます。

では上図を、実際の現象に即した説明に直します。下図をみてください。壁に太めの釘が刺さっています（この状況自体不可思議ですが置いときましょう）。棒の元端に穴を開けて、釘に引っ掛けました。

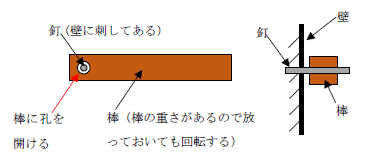
この状況こそが、「Q点を固定して自由に回転できる」の部分です。棒を固定しては回転しません。実際問題、固定されるのは釘などです。その釘に、孔を空けた棒を引っ掛けることで、自由に回転します。なお、棒自体の重さ（自重）があるので、放っておいても棒は下向きに回転します。

しかし、これでもまだ力のモーメントが何たるか理解できないはずです。棒が自由に回転できる状況で力を加えても、回転するのは当たり前だし、そもそも棒の自重で回転します。「力のモーメント」というくらいだから、物体の「質量」のように力の大きさを実感したいわけです。

力のモーメントと私たちの生活

さて、いよいよ力のモーメントの確信に迫りまります。力のモーメントが、私たちの生活にどうか変わっているのか考えましょう。

例えば、手でカバンを持つ時、力のモーメントの大きさを感じられます。下図をみてください。ある男性が両手を広げ、左手でカバンを持っています。

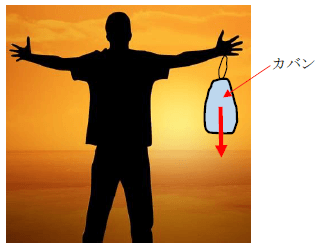
このとき、カバンの重量は下向きに作用します。実際にこの状態を試してみるとわかるのですが、腕に負担がかかるのが分かります。こんなに腕を広げて物を持つ人はいないはずです。

一方、今度は下図のように、肘を曲げ左腕の腕の長さを短くした状態でカバンを持ってみます。すると上図の状態よりも、いくらか腕の負担は減るはずです（実際に試すとよくわかります）。

この違いが、今回のテーマである「力のモーメント」の大きさなのです。再度、力のモーメントについて確認しましょう。力のモーメントの式は下記でした。

｢作用させる力×Q点からA点までの距離｣

つまり、カバンの重量は同じですが、腕の長さが短い分、力のモーメントは小さくなったのです。力のモーメントは、物体を回転させようとする力です。腕の力を抜けば、カバンの重量により腕は下方向へ回転するでしょう。腕が疲れるのは、その力のモーメントに対して筋肉が抵抗しているからです。

さて、もう１つ力のモーメントに関する例を説明します。それが「テコ」です。下図を見てください。

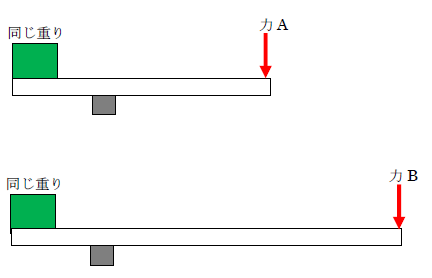
古来より、重い物を持ち上げるときテコが使われてきました。経験上、あるいは感覚的にわかると思いますが、同じ重りを持ち上げるとき、力Aと力Bでは、どちらが小さい力で重りを持ち上げられるのでしょうか。

答えは、力Bです。これも力のモーメントが関係しています。距離が長い分、力のモーメントが大きいので、小さな力で重りを持ち上げられるのです。詳細は下記も参考になります。

モーメントのつり合いとは？1分でわかる意味、考え方、重心位置の求め方は？

 

力のモーメントの計算方法と単位

ここまで説明すれば、力のモーメントが何か見えてきたと思います。ここからは力のモーメントの計算方法と、単位について説明します。下図を見てください。棒の先端にPという力が作用しています。「△」印は「支点」といって、回転はしますが水平、鉛直方向には動きません。

このときの、力のモーメントを求めてください。

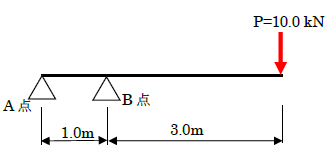
力のモーメントをMとすれば、

M=P×L＝10.0×3.0ｍ＝30.0　kN・ｍ

が力のモーメントです。つまり、下図の方向（B点を起点として時計回り）に力のモーメントが発生しています。

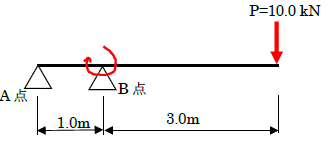
このような問題では、どこを起点に回転するのか考えると理解が早くなります。例えば上図の場合、10ｋNが作用するとB点を起点にして、棒は回転しますよね。

では、次の問題です。上記のモーメントが作用するとき、棒が回転しないためには、A点とB点にはどのくらいの力が作用するか求めてください。条件は下図です（最初の図と同じ）。

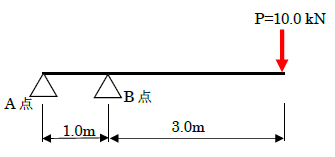
これは、力のモーメントの釣り合いの問題です。前述のように、力のモーメントはB点を起点にして、時計回りに30ｋNｍ作用していました。棒が回転しないためには、B点で力のモーメントが０になる必要があります。つまり下式を満足すべきです。

B点のモーメント＝時計回りに30ｋNｍ－反時計回りに30ｋNｍ＝０

反時計回りに30ｋNｍの力のモーメントが作用するためには、下式を計算すれば良いのです。

• A点の力（Fとする）×AB間距離（1.0ｍ）＝30ｋNｍ
• F×1.0＝30 ｋNｍ
• F＝30 ｋN

です。よって、下図のように力が作用することで、力のモーメントは釣合います。

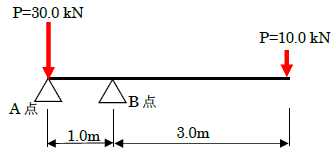
さて、例題から分かるように、力のモーメントの単位は下記となります。

力のモーメントの単位　N・m又はkN・m

モーメントの単位は、下記も参考になります。

モーメントの単位は？1分でわかる意味、読み方、換算、n・mm

角度のある力と、力のモーメント

では、力が鉛直方向に作用するのではなく、角度が付くとどうなるのでしょうか。下図を見てください。力が45度の方向に作用しています。このとき、B点に作用する力のモーメントを求めましょう。

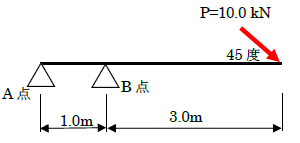
これは、数学で習ったベクトルを理解していれば大丈夫です。もし理解できていない人は、下記の記事を参考にしてください。角度のある力を分解する方法について、詳細に説明しています。

力の分解その計算方法

今回は簡単に説明しますが、斜めの力は鉛直と水平に分解すれば良いのです。45度のとき、ピタゴラスの定理より、鉛直・水平線に対する斜め線の比率は「1：1.41」でしたね。

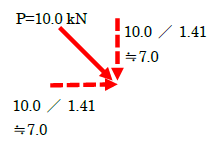
よって、力のモーメントは下記となります。

M＝10.0/1.41×3≒21.0　ｋNｍ

また別の方法でも算定可能です。力は斜めに作用したままで、作用する距離を水平ではなく斜め方向に変換します。すると下記となります。

M＝10.0×3/1.41≒21.0　ｋNｍ

両者の計算式を見てもらえば分かりますが、同じことですよね。また、角度が分かっていない場合は「cosθ」「sinθ」などで、力の方向あるいは距離の方向を変換すれば良いのです。

力のモーメントと偶力

次に力のモーメントと偶力を説明しましょう。偶力は教科書的に説明すれば、「ある点に対して、力の大きさが等しく、力の向きが反対で、力のモーメントが０にならない１組の力」です。

下図を見てください。左点は上方向に力が作用しています。物体A点に力のモーメントが作用すると考えてください。一方、右点は下方向に力が作用します。同じくA点にモーメントが作用します。

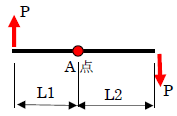
このとき左点の力により、時計回りの力のモーメントが発生します。一方、右点による力も、時計回りの力のモーメントが起きます。つまり、この物体Aは回転しますね。このような力を偶力といいます。

さて、偶力Pは物体Aを回転させます。つまり力のモーメントが作用するのです。偶力Pによる力のモーメントは、

M=P×(L1+ L2)

となります。偶力の意味は、下記が参考になります。

偶力の基礎知識と、モーメントの関係

偶力のモーメントとは？1分でわかる意味、公式、正負、力のモーメントとの違い

力のモーメントと曲げモーメントの違い

最後に、建築で学ぶ構造力学での注意点を説明します。前述してきた力のモーメントが作用するとき、「応力」と呼ばれる部材内部に力が発生しています。応力については下記を参考にしてください。

応力とは？1分でわかる意味と種類、記号、計算法

さて、応力には大まかに３つの種類があります。今回は説明を省きますが、その中に「曲げモーメント」があります。曲げモーメントは、物体内部に作用する力で、力のモーメントとは別物です。これを間違えないように注意しましょう。

曲げモーメントは下記が参考になります。

梁の曲げ応力度と誘導方法

曲げ応力とは？1分でわかる意味、公式と演習問題、単位、曲げ応力度

まとめ

今回は、力のモーメントについて説明しました。既に理解されている方は、クドイと思うくらい丁寧に説明したと思います。教科書的な計算式を理解した気になるのではなく、実現象として何が起きているのか理解すると、知恵として身に付きますよ。

モーメントの単位、偶力の意味など併せて勉強しましょうね。

モーメントの単位は？1分でわかる意味、読み方、換算、n・mm

偶力のモーメントとは？1分でわかる意味、公式、正負、力のモーメントとの違い

力のモーメントの正負とは？1分でわかる意味、公式、力のモーメントの和に関する例題

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

▼スポンサーリンク▼

【初回資料が今だけ無料！】1日約13円で情報をアップデート！

有料メルマガを無料で見てみませんか？⇒　忙しい社会人、学生のためのビルディング・アップデート

更新情報

• 当サイトでは、ほぼ毎日、記事更新・追加を行っております。


• 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。


• 新着記事一覧

プロフィール

• 
• 略歴▼
• 名前　ハナダユキヒロ/MITUME lab代表.
• 2010年　弊サイトを開設
• 2010～2017年　国立大学大学院修了
• 2017年12月に当HPが書籍化。
• 「わかる構造力学」
• 2022年4月に「わかる構造力学」の改訂版出版。
• 「わかる構造力学(改訂版)」


• 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。


• 当サイトの目的▼
• 建築学生が学ぶ「構造力学」の目的


• とりあえず10記事▼
• 初めましての方に10記事用意しました


• おすすめ書籍紹介▼
• ハナダユキヒロが建築関連書籍の良書を選びました

建築の本、紹介します。▼

▼【好評！】管理人おすすめ▼

• あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！

同じカテゴリの記事一覧

• 力のモーメントの正負とは？1分でわかる意味、公式、力のモーメントの和に関する例題
• 腕の長さとは？1分でわかる意味、モーメントの関係、作用点、向きの関係
• 合モーメントとは？1分でわかる意味、正負、モーメントの合成と計算方法
• 回転方向とは？1分でわかる意味、右回りと左回りの覚え方、正負の考え方
• モーメントのつり合いとは？1分でわかる意味、考え方、重心位置の求め方は？
• 力とは何か？3分でわかる意味、物体の移動、回転、変形との関係
• 力の3要素とは？1分でわかる意味、力の大きさ、作用点、方向
• 力の合成とその計算方法
• 力の分解その計算方法
• 合力とは？1分でわかる意味、読み方、求め方、角度との関係