構造図解で一発理解建築用語サクッと理解構造力学が苦手おすすめ書籍おすすめPDF教材 noteで学ぶ

HOME > 構造力学の基礎 > 反力とは？支点の種類・求め方と鉛直反力の計算を解説【図解】

反力とは？支点の種類・求め方と鉛直反力の計算を解説【図解】

この記事の要点

反力とは、荷重（外力）に対して支点に生じる力のことで、建築物が静止している状態では荷重と反力の合計が必ずゼロになる。

支点の種類（ローラー・ピン・固定端）によって生じる反力の向きと数が異なるため、支点の条件を正しく把握することが反力計算の出発点となる。

この記事では、反力とは何か、どのような支点があるのかを整理します。

反力とは、荷重（外力）に対して支点に生じる力です。構造物が静止する（動かない）とき、

荷重の合計と反力の合計を足し合わせると必ずゼロ、すなわち「力が釣り合う」状態になります。

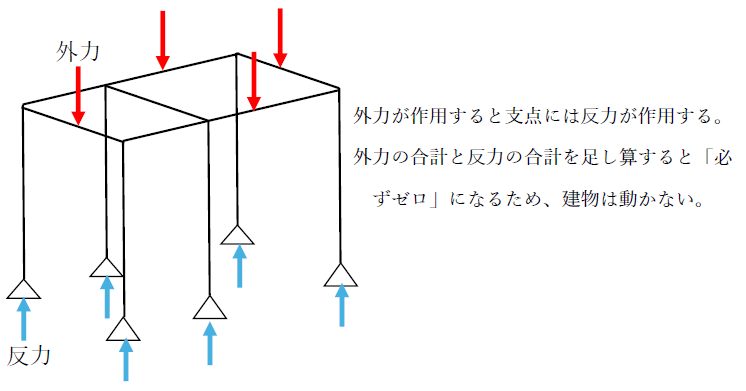
反力の意味

当然、私たちが利用する建物は通常「静止した状態」です。よって、建物に生じる荷重と反力は釣り合っているのです。支点の意味は下記をご覧ください。

支点とは？意味・種類の違い【図解】｜ローラー・ピン・固定端

支点を理解すれば構造力学がわかる：ピン・ローラー・固定の違いと反力

次に反力を身近な生活からイメージしましょう。部屋に机があります。机の脚は四本です。

机の上にはPCやマグカップが置いています。それらの質量は、重力により下向きの荷重として作用します。

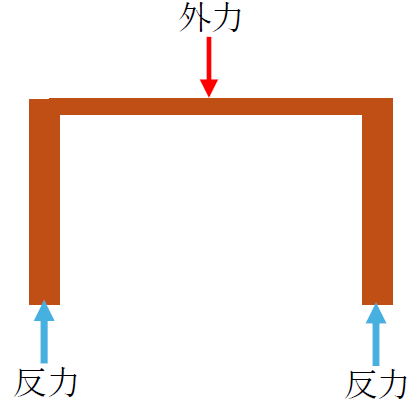
反力を身近な物からイメージする

普段私達は意識していませんが、机が静止するためには、机の４つの脚に対して、下向きの荷重とは逆方向（上向き）の力が作用しています。

なお、反力は構造物の支点に生じるので「支点反力（してんはんりょく）」ともいいます。

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

基礎と支点、反力の関係

では前述した「支点（してん）」とは何でしょうか。支点は構造物の基礎等をモデル化したものです。

基礎は、建築物を支える構造部材です。基礎のように支える部分を点としてモデル化しています。

基礎が無ければ建築物として成立しないように、いかなる構造モデルも支点がなければ成立しません。

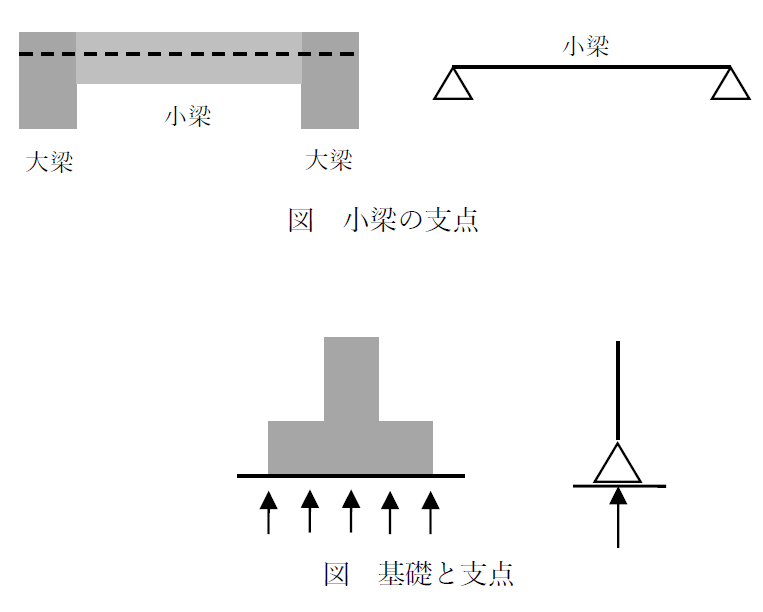
なお、基礎だけが支点になるわけではなく、たとえば、小梁は大梁に接合するため、大梁を小梁にとっての支え（支点）として考えます。

また、支点はモデル化に過ぎません。なお、図に示すように、実際は、基礎などは点ではなく面で支えています。

基礎と支点、反力の関係

引越しで重い荷物を両手で運ぶことを想像してください。荷物が落ちないように両手でしっかり「支えている」でしょう。

荷物の重さを両手で支えるには、両手に力を入れて荷物を押し返す必要があります。

このように支点には外力に抵抗する力が作用し、これが支点反力（反力）なのです。

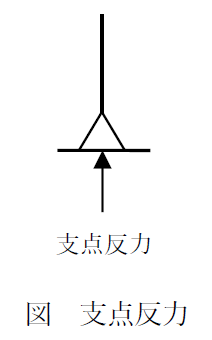
荷物を支える手を離すと、荷物はただちに落下します。すなわち、支点は部材の移動を拘束する役割があり、移動が拘束される方向には反力が作用するのです。

なお、支点の移動が拘束されるということは「支点の変位＝0（支点は動かないこと）」を意味します。

支点の種類と反力の向き

一般的に、支点は下表に示す３つに分類されます。

表　支点の種類

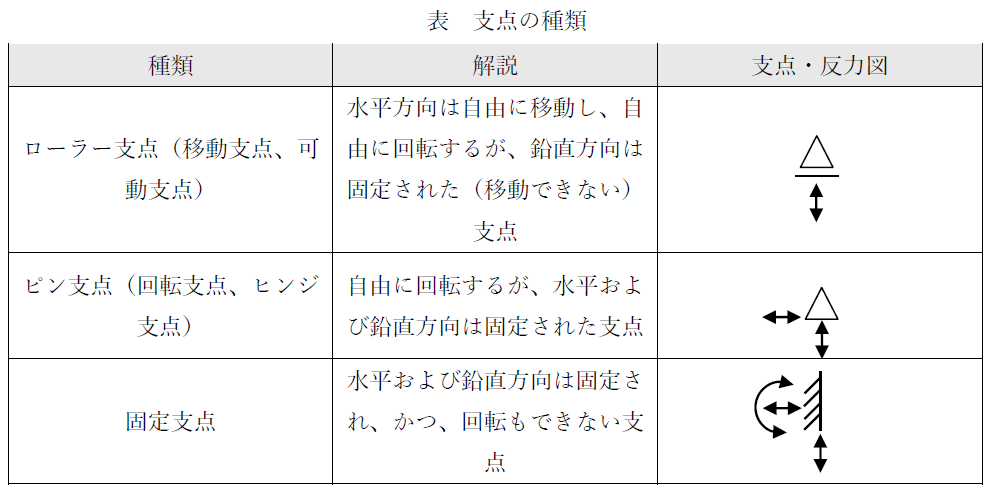
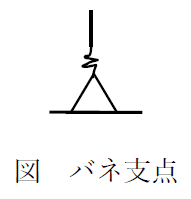
なお、上表の他にバネの性質をもった支点（バネ支点または弾性支承という）があります。

バネはある程度のかたさを持っていて、力を加えると反力を返しながら変形します。つまりバネ支点は、変形しながら力を支えます※。

バネ支点

それでは各支点の特徴と反力の向きを解説します。

ローラー支点（移動支点、可動支点）

台車やスーツケースは車輪（コロ）が付いているため、押している手を離しても勝手に移動します。

現実には床と車輪に働く摩擦力（抵抗力）により、自然に移動は止まりますが、ローラー支点は水平力に一切抵抗できないと考えます。

図のように、水平力が作用する両端をローラー支点とした梁を考えます。このとき、ローラー支点は水平力に抵抗できないので、梁は加力方向に移動するでしょう。

ローラー支点

さらに、ローラー支点は回転方向にも自由に移動できます。よって、ローラー支点に生じる反力は「鉛直方向の反力（一方向の反力）のみ」です。

なお、下図のような構造物は力に対して「静止しない」不安定な構造として扱います。

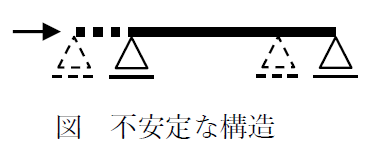
不安定な構造

ローラー支点では鉛直反力のみ生じると書きましたが、

下図のようにローラー支点を90度回転させて配置した場合、鉛直方向に自由に移動する支点となり、反力は水平方向に生じます。

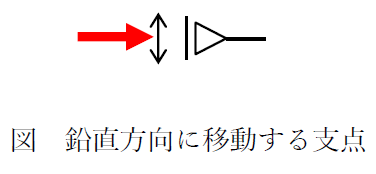
鉛直方向に移動する支点

ローラー支点の詳細は下記をご覧ください。

ローラー支点とは？1分でわかる意味、具体例、モーメントとの関係、ピン支点との違い

ピン支点（回転支点、ヒンジ支点）

下図のように、ピン支点では水平・鉛直方向に力をかけても移動しません。すなわち、ピン支点には鉛直反力と水平反力の２方向の反力が生じます。

ピン支点

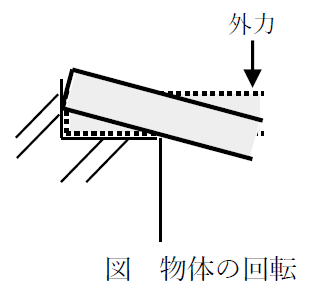
下図のように物体の端部を下向きに押すと少しの力で落下します。

このように、ピン支点ではモーメントが作用すると自由に回転します。これは回転方向に自由に移動することを意味します。

ピン支点の詳細は下記をご覧ください。

ピン支点とは？1分でわかる意味、モーメント反力との関係、ローラー支点、固定支点との違い

固定支点（固定端）

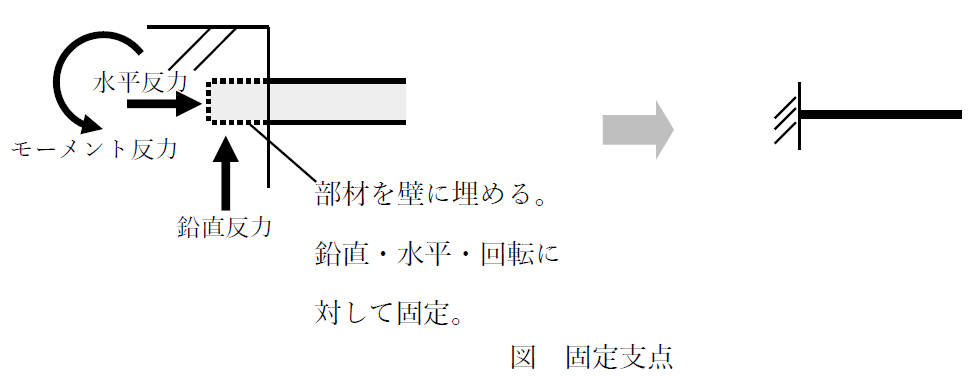
固定支点では水平、鉛直、回転の全てが拘束されるため、１端を固定支点とするだけで構造物が安定します。反力は３方向（鉛直、水平、回転）に生じます。

固定支点

固定支点の詳細は下記をご覧ください。

固定支点とは？反力・モーメントの意味とピン支点・ローラー支点との違い（図解）

支点の変位と反力の関係

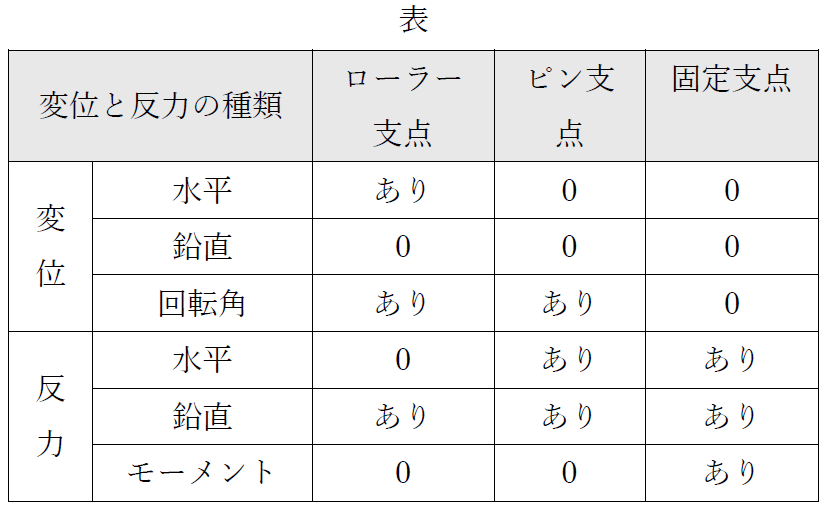
前述の支点に生じる変位、反力の関係を整理して示します。下表の通り、支点の変位が拘束される場合に反力が生じます。逆に支点の移動が自由であれば反力がゼロです。

変位と反力の種類

反力の求め方

反力の求め方は「力のつり合い条件」を用います。名前だけ聞くと難しそうですが、前述した話そのものです。

構造物が静止するとき、外力の合計と反力の合計を足し合わせると「必ずゼロ」になります。

この性質を「方向別」に整理するのです。力の方向には

・鉛直方向

・水平方向

・回転方向

があります。それぞれの方向で力はつり合うので下記の等式が成り立ちます。

力のつり合い条件

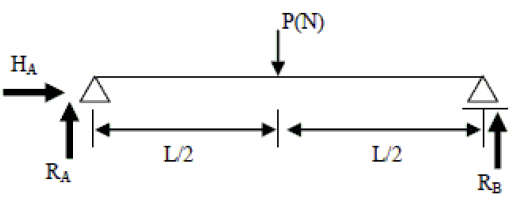
実際に下図の例題について、それぞれの方向の力のつり合いを考えます。例題の左支点はピン支点、右支点はローラー支点です。

反力を求める前に、あらかじめ反力の向きを決めておきます。ここでは水平反力は右向き、鉛直反力は上向きとして仮定します。

反力の求め方

水平方向のつり合い

水平力が作用する梁について力のつり合いを考えます。上図の構造物は、外力として水平力は作用していません。

よって、ΣH=0の関係式を考えると、

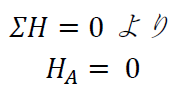
水平方向のつり合い

ですね。外力が作用していないわけですから、当然、反力もありません。ちなみに、力のつり合いを考える場合、どちらが正でも良いです。

ただし、正の値と決めた方向の逆方向は必ず負の値となるように定義しましょう。

鉛直方向のつり合い

次に、鉛直方向のつり合いを考えます。

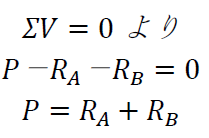
鉛直方向のつり合い

だとわかります。

モーメントのつり合い

さて、問題はここです。モーメントのつり合いを考えます。モーメントの定義は｢支点からの距離×作用する力｣です。

前述したように、ピン支点は回転変位が自由のためモーメントは生じません。よって、A点でのモーメントのつり合いはゼロになります。

モーメントのつり合い

A点を基準にモーメントのつり合いを考えると、まず中央に作用する力があるので、このモーメントは

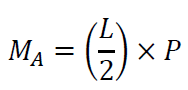
M_A=(L/2)×P

です。さらに、反力RBが逆向きの力を作用させていますから

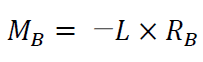
M_B=－L×R_B

です。

(L/2)×P－L×R_B=0

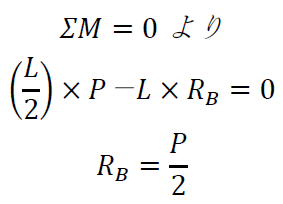
です。また、鉛直方向の力のつり合いから

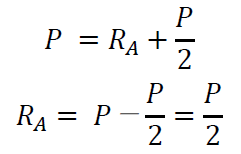
P =R_A+P/2

になります。今回は最も簡単な例題を通して反力の求め方を解説しました。

支点の条件、外力の条件により、計算のパターンはいくらか変わります。色々な例題を通して反力の求め方を練習しましょう。

梁の反力の求め方｜つり合い条件式と演習問題で計算を身につける

混同しやすい用語

反力

外力（荷重）に対して支点が抵抗するために生じる力のこと。

ローラー支点・ピン支点・固定端など支点の種類によって生じる反力の方向と数が変わる。

外力（荷重）が「建物に作用する力」であるのに対し、反力は「支点が外力に抵抗するために発生する力」という点で向きが逆になる。

外力（荷重）

建物の外部から作用する力で、固定荷重・積載荷重・風荷重・地震荷重などが代表的。

構造解析では力の大きさと作用方向を明確にする。

反力は外力に対して生じる「応答」であるため、外力の大きさ・方向が決まれば釣り合い条件式（ΣH＝0・ΣV＝0・ΣM＝0）から反力を求められる。

試験での問われ方｜管理人の一言

一級建築士試験では「支点の種類と反力の方向・数」の組み合わせが基本問題として頻出であり、ローラー（1方向）・ピン（2方向）・固定端（3方向）の違いを正確に覚えることが合格への近道となる。

反力の求め方は釣り合い条件式を使うだけだが、まず支点条件と荷重の向きを図示することで式の立て間違いが防げるため、図を描く習慣を身につけよう。

反力を整理した表を示します。

項目	内容	備考
ローラー支点	1方向の反力（鉛直方向のみ）が生じる	水平移動は自由。回転も自由
ピン支点	水平・鉛直の2方向の反力が生じる	回転は自由。移動は拘束
固定端	水平・鉛直・モーメントの3方向の反力が生じる	移動も回転もすべて拘束