等差数列の公式は？3分でわかる公式、覚え方、等差数列の和の計算
7/1最新版入荷！一級建築士対策も◎！290名以上の方に大好評の用語集はこちら⇒ 全92頁！収録用語1100以上！建築構造がわかる専門用語集
等差数列（とうさすうれつ）の一般項を求める公式は「an=a+(n－1)d」です。また、等差数列の和の公式はn(a+an)/2で算定されます。anはｎ番目の項、ｄは公差、aは初項です。公差とは等差数列における一定の数ｄです。今回は等差数列の公式、覚え方、等差数列の和の計算について説明します。公差の意味は下記が参考になります。
【無料自己分析】あなたの本当の強みを知りたくないですか？⇒ 就活や転職で役立つリクナビのグッドポイント診断
等差数列の公式は？
等差数列の公式（一般項を求める、等差数列の和の計算）には下記があります。
anはｎ番目の項、aは初項、ｎは数列における項の数、ｄは公差です。上記の公式にあてはめれば、等差数列における各値を算定できます。
なお、公差とは等差数列における一定の数ｄのことです。等差数列では「a,a+d,a+2d…」のように項が変化します。このとき「2番目の項－初項＝a+d－a=d」のように、順番に項の差をとると一定の値になります。これが公差です。公差の詳細は下記が参考になります。
等差数列の公式の覚え方
「等差数列はどのような数列か？」理解すれば、公式も自然と覚えられるでしょう。
等差数列は「a,a+d,a+2d…」のように、初項に一定の値ｄを加えて増えていく数列です。まずは数列の意味を理解してください。
一般項を求める公式は、簡単な数列をイメージすると良いでしょう。例えばn=2の項はa+dです。どうすればnという文字を考慮して「a+d」になるか考えると「a+(n－1)d」が導けます。
等差数列の和の計算
前述した公式を使って、実際に等差数列の和を計算しましょう。
下記の等差数列の和を計算してください。
1,2,3…10
2,4,6…20
1問目から解きます。まず数列の公差を求めます。
2－1＝1なのでｄ＝1、n=10、a=1です。まず一般項anを求めます。
よって
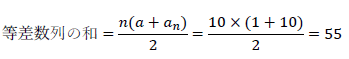
です。２問目も同様の流れで解きます。
4－2＝2なのでｄ＝2、n=20÷2=10、a=2です。まず一般項anを求めます。
よって
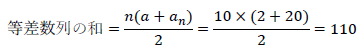
です。
まとめ
今回は等差数列の公式について説明しました。等差数列の公式は暗記すると便利です。ただし、まずは等差数列の意味を理解しましょう。意味を理解すれば公式を忘れても思い出せます。公差の意味など下記も勉強しましょうね。
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
▼スポンサーリンク▼
▼【好評！】管理人おすすめ▼
- あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！
▼用語の意味知らなくて大丈夫？▼
▼同じカテゴリの記事一覧▼
- 等比数列の一般項は？1分でわかる求め方、和の計算、等差数列との違い
- 公差とは？1分でわかる意味、一般項、n項、等差数列との関係
- 公比とは？1分でわかる意味、求め方、公差との違い、等比数列の公式
- 一般項とは？1分でわかる意味、求め方、末項との違い、一般項の和との関係
- 初項とは？1分でわかる意味、末項、一般項との違い、公比と公差との関係、第n項までの和
- 初項の求め方は？1分でわかる意味、等比数列と等差数列での求め方、一般項、末項との違い
▼カテゴリ一覧▼
▼他の勉強がしたい方はこちら▼
【好評】LINEで質問！
管理人に質問してみる？
わかる1級建築士の計算問題解説書
【初回資料が今だけ無料！】1日約13円で情報をアップデート！
有料メルマガを無料で見てみませんか？⇒ 忙しい社会人、学生のためのビルディング・アップデート
わかる2級建築士の計算問題解説書！
【30%OFF】一級建築士対策も◎！構造がわかるお得な用語集
更新情報
- 当サイトでは、ほぼ毎日、記事更新・追加を行っております。
- 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。
- 新着記事一覧
プロフィール
- 略歴▼
- 名前 ハナダユキヒロ/MITUME lab代表.
- 2010年 弊サイトを開設
- 2010～2017年 国立大学大学院修了
- 2017年12月に当HPが書籍化。
- 「わかる構造力学」
- 2022年4月に「わかる構造力学」の改訂版出版。
- 「わかる構造力学(改訂版)」
- 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。
- 当サイトの目的▼
- 建築学生が学ぶ「構造力学」の目的
- とりあえず10記事▼
- 初めましての方に10記事用意しました
- おすすめ書籍紹介▼
- ハナダユキヒロが建築関連書籍の良書を選びました
建築の本、紹介します。▼
▼【好評！】管理人おすすめ▼
- あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！
同じカテゴリの記事一覧
- HOME > 数学の基礎 >等差数列の公式は？3分でわかる公式、覚え方、等差数列の和の計算
- 1級の過去問(計算)解説
- 限定メルマガ
- わかる建築構造の用語集・図解集
- 1頁10円！PDF版の学習記事