片持ち梁の最大曲げ応力は？1分でわかる求め方、例題、応力と位置の関係
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
片持ち梁の最大曲げ応力Mは「M＝PL（先端集中荷重作用時）」「M＝wl^2/2（等分布荷重作用時）」です。荷重条件で最大応力の値が変わります。1種類の荷重が作用する場合、「先端に集中荷重が作用する場合」が最も曲げ応力が大きくなります。今回は片持ち梁の最大応力の求め方、例題、応力と位置の関係について説明します。片持ち梁、最大曲げ応力の詳細は下記が参考になります。
最大曲げモーメントとは？1分でわかる意味、求め方と例題、集中荷重、片持ち梁、両端固定梁の計算
100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒ いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事
片持ち梁の最大曲げ応力は？求め方、応力と位置の関係
片持ち梁の最大曲げ応力Ｍは「Ｍ＝PL（先端集中荷重作用時）」「Ｍ＝wL^2/2（等分布荷重作用時）」等です
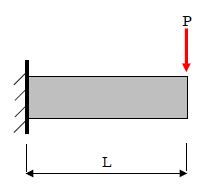
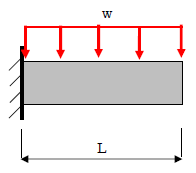
上図のように、片持ち梁の最大応力は「荷重条件」によって変わります。なお、1種類の荷重が作用する場合「先端に集中荷重の作用する」ときの曲げ応力が最も大きくなります。
例として、先端集中荷重と等分布荷重による最大曲げ応力の違いを確認しましょう。
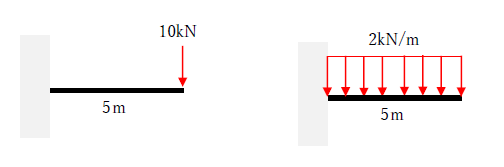
等分布荷重ｗは、ｗＬ＝Ｐとなるよう設定したのでＰ＝10kN、Ｌ＝5m、w=2kN/mです。各片持ち梁の最大曲げ応力は下記の通りです。
・先端集中荷重の作用する片持ち梁 ⇒ M=PL=10×5＝50kNm
・等分布荷重の作用する片持ち梁 ⇒ M=wL^2/2=2×5^2/2=25 kNm
荷重の大きさは同じにも関わらず「先端集中荷重」の方が2倍も曲げ応力が大きくなりましたね。
下図をみてください。等分布荷重は「集中荷重に変換」できます。集中荷重に変換すると「等分布荷重の作用幅の中央」に荷重が作用しています。
集中荷重による曲げ応力は「M＝PL」です。よって、Lが大きいほどMは大きくなり、Lが小さければMも小さくなります。
等分布荷重は「梁の中央に作用する集中荷重」と同じ条件なので、曲げ応力が半分も小さいのです。
以上より、片持ち梁の最大曲げ応力は「荷重の位置」で大きく変わります。固定端からより離れた距離に荷重が作用するほど最大曲げ応力は大きくなるでしょう。
単純な事実ですが、構造設計の実務でも応用できます。例えば、片持ち梁先端から全ての力を伝達するのではなく、複数の部材を介して力を伝達することで、最大曲げ応力を「小さくする」などです。
下図に色々な荷重条件による片持ち梁の最大曲げ応力を示しました。
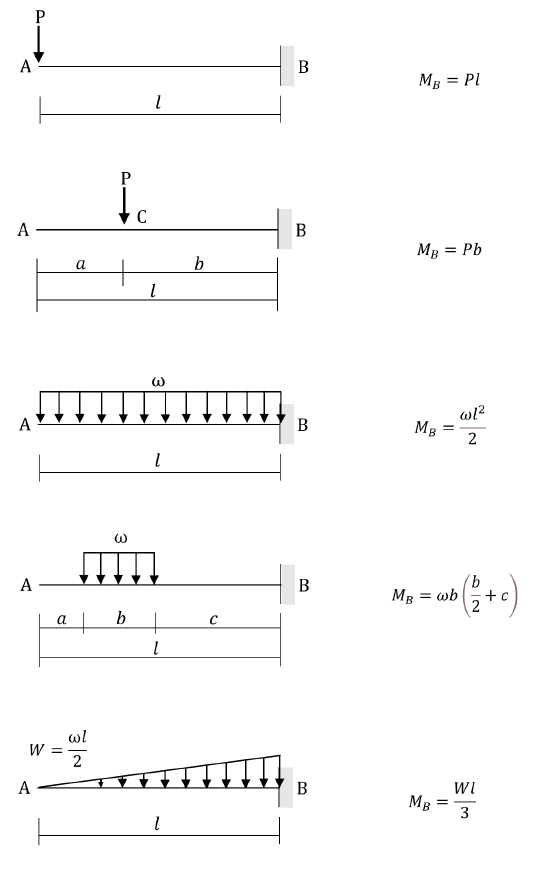
先端集中荷重と比較して「どのくらい応力が小さくなるのか」を調べてみましょうね。片持ち梁の意味、応力の求め方など下記も参考になります。
片持ち梁の最大曲げ応力と例題
例題として、下図に示す片持ち梁の最大曲げ応力を求めてください。
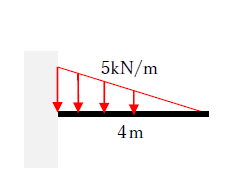
前述した公式を使っても良いのですが、三角形分布荷重も集中荷重に変換できます（三角形の面積を算定する）。変換の方法は下記が参考になります。
三角形分布荷重とは？1分でわかる意味、作用点、集中荷重との関係、片持ち梁
上図の三角形分布荷重を集中荷重に変換すると「5kN/m×4m/2＝10kN」です。また、変換した集中荷重の作用する位置は、三角形の重心位置（作用長さの1/3）です。
よって、最大曲げ応力＝10kN×4m/3=40/3=13.3kNmとなります。
まとめ
今回は、片持ち梁の最大曲げ応力について説明しました。片持ち梁の最大曲げ応力Mは「M＝PL（先端集中荷重）」「M=wL^2/2（等分布荷重）」です。その他、荷重条件により最大応力の値は変わります。まずは片持ち梁の特徴を勉強しましょう。下記が参考になります。
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
▼スポンサーリンク▼
▼【好評！】管理人おすすめ▼
- あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！
▼用語の意味知らなくて大丈夫？▼
▼同じカテゴリの記事一覧▼
- 片持ち梁とは？1分でわかる構造、様々な荷重による応力と例題
- 片持ち梁の応力は？1分でわかる種類、公式、計算方法
- 片持ち梁のモーメントは？1分でわかる計算、公式、荷重との関係、モーメントとせん断力の求め方
- 片持ち梁の曲げモーメント図は？1分でわかる書き方、公式、計算、三角分布荷重との関係
- 集中荷重が作用する片持ち梁とは？1分でわかる計算、反力、応力、たわみの求め方
- 等分布荷重が作用する片持ち梁とは？3分でわかる計算、応力、せん断力、たわみ、公式、モーメント図
- 片持ち梁の最大モーメントを求める
▼カテゴリ一覧▼
- 建築物と構造力学の関係(まずは、苦手な勉強の進め方から)
- モデル化を学ぶ(まずは、構造物のモデル化から)
- 静定構造物の解き方を学ぶ(まずは、静定構造物に関する基礎用語から)
- 断面の性質を学ぶ(まずは、断面図形に関する基礎用語から)
- 梁のたわみを学ぶ(まずは、梁のたわみと基礎用語から)
▼他の勉強がしたい方はこちら▼
【好評】LINEで質問！
管理人に質問してみる？
わかる1級建築士の計算問題解説書
【初回資料が今だけ無料！】1日約13円で情報をアップデート！
有料メルマガを無料で見てみませんか？⇒ 忙しい社会人、学生のためのビルディング・アップデート
わかる2級建築士の計算問題解説書！
【30%OFF】一級建築士対策も◎！構造がわかるお得な用語集
更新情報
- 当サイトでは、ほぼ毎日、記事更新・追加を行っております。
- 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。
- 新着記事一覧
プロフィール
- 略歴▼
- 名前 ハナダユキヒロ/MITUME lab代表.
- 2010年 弊サイトを開設
- 2010～2017年 国立大学大学院修了
- 2017年12月に当HPが書籍化。
- 「わかる構造力学」
- 2022年4月に「わかる構造力学」の改訂版出版。
- 「わかる構造力学(改訂版)」
- 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。
- 当サイトの目的▼
- 建築学生が学ぶ「構造力学」の目的
- とりあえず10記事▼
- 初めましての方に10記事用意しました
- おすすめ書籍紹介▼
- ハナダユキヒロが建築関連書籍の良書を選びました
建築の本、紹介します。▼
▼【好評！】管理人おすすめ▼
- あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！
同じカテゴリの記事一覧
- HOME > 構造力学の基礎 > 片持ち梁の最大曲げ応力は？1分でわかる求め方、例題、応力と位置の関係
- 1級の過去問(計算)解説
- 限定メルマガ
- わかる建築構造の用語集・図解集
- 1頁10円！PDF版の学習記事