- 【無料お試しキャンペーン中！】1級・2級建築士試験の構造の疑問を気軽に相談 初心者でもわかる！1級・2級建築士試験(構造)相談カフェ
- 管理人が業界分析！1日13円で建築業界がわかるLINE配信！ ⇒ まずはリンクをクリックして友だち追加！
モーメントのつり合いとは？1分でわかる意味、考え方、重心位置の求め方は？
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
モーメントのつりあいとは、ある点における力のモーメント（物体を回転させようとする力）の総和です。モーメントのつり合いが0になるとき、物体は静止します。モーメントのつりあいは、構造力学で最も重要な法則の１つです。モーメントのつりあいの考え方を元に重心の算定、断面一次モーメントも定義できます。今回は、モーメントのつり合いの意味、考え方、重心位置の求め方について説明します。力のモーメント、重心の求め方など下記も参考になります。
力のモーメントってなに？本当にわかるモーメントの意味と計算方法
モーメントから重心を求める方法は？1分でわかる計算、モーメントのつりあい
100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒ いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事
モーメントのつり合いとは？考え方
モーメントのつり合いとは、ある点における力のモーメント（物体を回転させようとする力）の総和です。つまり、モーメントのつり合いが0になるとき物体は静止します。
モーメントのつり合いの考え方を解説します。下図に示すような、支点と梃（てこ）を用いて物体の質量を比較する器械を天秤（てんびん）といいます。
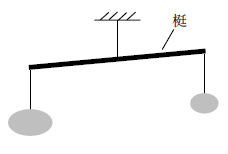
天秤は下図に示すように、梁と１つのピン支点からなる構造物と力学的には同じです。
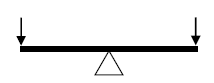
下図に示すように、質量WA、WBが作用してつりあうとき、ΣH=0、ΣV=0、ΣM=0が成り立ちます。
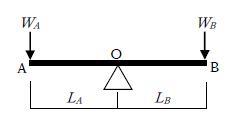
ピン支点でのモーメントは0なので、物体A、Bの重さをWA、WB、物体の重心位置から支点までの距離をLA、LBとすると、点Oでのモーメントのつりあいは下式となります（※ただし、てこの変形は考えない）。
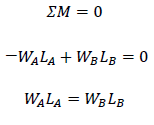
点Aを中心にモーメントのつりあいを求めても上式は成立します。まずはピン支点の支点反力Rを求めます。鉛直方向の力はつりあうので、
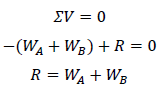
となります。※なお、下向きの力を負値、上向きの力を正値と考える。点Aのモーメントのつりあいは、
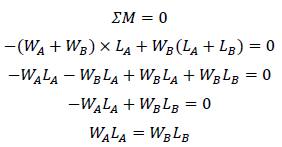
です。WA+WBは各重さの合力なので、上式は合力によるモーメントと各部分の重さによるモーメントの合計が等しい（つりあう）ことを意味します。
さて、上式を比率の関係で表すと
となります。天秤がつりあうとき、重さの比率と距離の比率は等しくなければいけません。前述の図に示す天秤がつりあうとき重さWAの値を求めると
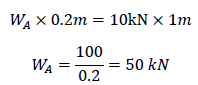
となります。つまりWAは10kNに対して5倍もの質量でないとつりあいません。見方を変えれば10kNで50kNの力を生み出せることを意味します。式5.4または小さな力で大きな力を生み出す原理を、てこの原理ともいいます。
モーメントのつり合いと重心位置の求め方は？
前述より、ある点における各力のモーメントの総和は、合力のモーメントと等しくなります。合力は重心位置に作用するので、各力によるモーメントと合力の値が分かれば、合力の作用点すなわち重心位置が算定できます。
たとえば下図に示す重心位置は下式のように求められます。
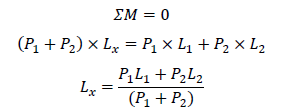
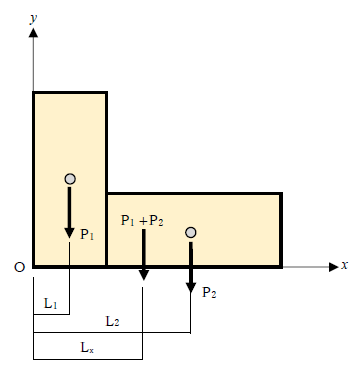
なお、上式の分子「P1L1+P2L2」を断面について定義した値が断面一次モーメントです。重心、断面一次モーメントの詳細は下記が参考になります。
まとめ
今回は、モーメントのつり合いについて説明しました。モーメントのつり合いとは、ある点における力のモーメントの総和です。モーメントのつり合いが0になるとき物体は静止します。力のモーメント、断面一次モーメント、重心位置など下記も勉強しましょう。
力のモーメントってなに？本当にわかるモーメントの意味と計算方法
モーメントから重心を求める方法は？1分でわかる計算、モーメントのつりあい
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
▼人気の記事ベスト３▼
- 1.断面係数の計算方法を本当にわかっていますか？→断面係数とは？
- 2.丸暗記で良いと思ったら大間違い→断面二次モーメントとは何か？
- 3.違いを適切に説明できますか？→等分布荷重とは？集中荷重との違いや使い方について
▼用語の意味知らなくて大丈夫？▼
▼同じカテゴリの記事一覧▼
- 力のモーメントってなに？本当にわかるモーメントの意味と計算方法
- 力のモーメントの正負とは？1分でわかる意味、公式、力のモーメントの和に関する例題
- 腕の長さとは？1分でわかる意味、モーメントの関係、作用点、向きの関係
- 合モーメントとは？1分でわかる意味、正負、モーメントの合成と計算方法
- 回転方向とは？1分でわかる意味、右回りと左回りの覚え方、正負の考え方
- 力とは何か？3分でわかる意味、物体の移動、回転、変形との関係
- 力の3要素とは？1分でわかる意味、力の大きさ、作用点、方向
- 力の合成とその計算方法
- 力の分解その計算方法
- 合力とは？1分でわかる意味、読み方、求め方、角度との関係
▼カテゴリ一覧▼
- 建築物と構造力学の関係(まずは、苦手な勉強の進め方から)
- モデル化を学ぶ(まずは、構造物のモデル化から)
- 静定構造物の解き方を学ぶ(まずは、静定構造物に関する基礎用語から)
- 断面の性質を学ぶ(まずは、断面図形に関する基礎用語から)
- 梁のたわみを学ぶ(まずは、梁のたわみと基礎用語から)
- 座屈を学ぶ(まずは、座屈-基礎用語-から)
▼他の勉強がしたい方はこちら▼
【読まれています】管理人による建築業界の分析！
1日13円で建築業界がわかるLINE配信！。
わかる1級建築士の計算問題解説書
あなたは数学が苦手ですか？
【有料メルマガの初回資料が今だけ無料！】1日約13円で情報をアップデート！
有料メルマガを無料で見てみませんか？⇒ 忙しい社会人、学生のためのビルディング・アップデート
わかる2級建築士の計算問題解説書！
【30%OFF】一級建築士対策も◎！構造がわかるお得な用語集
更新情報
- 当サイトでは、ほぼ毎日、記事更新・追加を行っております。
- 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。
- 新着記事一覧
プロフィール
- 略歴▼
- 名前 ハナダユキヒロ/MITUME lab主宰.（筆者のコラムはこちら）
- 2010年 弊サイトを開設
- 2010～2017年 国立大学大学院修了
- 2017年12月に当HPが書籍化。
- 「わかる構造力学」
- 2022年4月に「わかる構造力学」の改訂版出版。
- 「わかる構造力学(改訂版)」
- 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。
- 自己紹介▼
- 建築学生が学ぶ「構造力学」とは？
- とりあえず10記事▼
- 初めましての方に10記事用意しました
- おすすめ書籍紹介▼
- ハナダユキヒロが建築関連書籍の良書を選びました
建築の本、紹介します。▼
同じカテゴリの記事一覧
- HOME > 構造力学の基礎 > モーメントのつり合いとは？1分でわかる意味、考え方、重心位置の求め方は？
- 1級の過去問(計算)解説
- 限定メルマガ
- わかる建築構造の用語集・図解集
- 1頁10円！PDF版の学習記事