2軸方向に生じる応力の計算方法｜任意断面の応力と力のつりあい

この記事の要点

FEM解析で複雑な荷重を受ける板要素を設計するとき、2軸方向の応力が同時に生じる。

「どの方向の断面で最も大きな応力が出るか」を知るために、任意断面の応力計算が必要になる。

2軸応力（平面応力状態）では、σx・σy・τxyの三成分から任意角θの断面の応力を計算できる。

変換式またはモールの応力円を使えば、最大主応力方向が特定できる。

2軸応力状態から主応力（最大・最小垂直応力）を求めるには、モールの応力円を用いる方法が有効で、建築士試験でも出題される重要な考え方。

【管理人おすすめ！】セットで3割もお得！約1,100語の用語集＋476点の図解集セット⇒　建築構造がわかる基礎用語集＆図解集セット

2軸方向の応力状態では、x・y各軸方向の垂直応力とせん断力が同時に作用します。

２次元の四角形の物体には、各面にx軸およびy軸（2軸）の各軸方向に生じる垂直応力、各軸と直交する方向に生じるせん断力が生じます。

この四角形から微小直角三角形要素を取り出し、三角形要素の斜辺に生じる垂直応力、せん断力を求めれば、任意の傾きをもつ断面に生じる応力が算定できます。

今回は、2軸方向の応力状態、任意断面の応力の求め方と力のつりあいについて説明します。

一次元物体の任意断面の応力、三次元物体の力のつりあいは下記が参考になります。

任意断面の応力とは｜斜め断面の垂直応力とせん断応力の計算方法

応力の平衡方程式とは？意味・導出と有限要素法・弾性力学への応用（座標軸別の式）

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

2軸方向に生じる応力とは？

２次元の四角形の物体には、下図に示すように2軸方向（x、ｙ軸方向）に生じる垂直応力、各面に平行に作用するせん断力が生じます。

２次元物体に生じる応力状態を下図に示します。

※ここでいう応力とは構造力学における「応力度（単位面積当たりの断面力）」とする。

また、物理学などでは「断面力を合応力」、建築構造力学では「断面力のことを応力」という。

なお、四角形物体は平面でz方向（奥行）の長さは1、ｚ方向の応力、ひずみは考えません。

また、簡単のため力の矢印を１本で図示していますが、各応力は各面に「分布」しています。

たとえば、σyに「面積（dz×dx＝1×dx=dx）」を掛け算すれば「σydx」となり、断面力（※構造力学でいう応力）の値に変換できます。

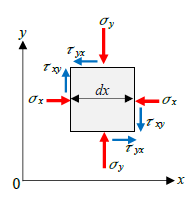
2軸方向の応力状態

当然、実際の物体は3次元（立体）ですが、２次元（面）の問題として扱うことで、比較的簡単に力のつり合いや、後述する任意断面に生じる垂直応力、せん断力などが算定できます。

なお、構造力学では、一般に用いる構造部材の特性上、さらに変数を減らして1次元（線）の応力状態を考えることも多いです（梁、柱の応力）。

1次元物体の任意断面に生じる応力の詳細は下記をご覧ください。

任意断面の応力とは｜斜め断面の垂直応力とせん断応力の計算方法

さて、下図に示す四角形物体から微小な直角三角形要素を取り出します。

三角形要素の斜面は鉛直線から任意の角度θ傾いており、θを小さくあるいは大きくすることで斜面の勾配も変わります（すなわち斜面は任意断面）。

次に、斜面（任意断面）に垂直応力σ、せん断力τが下図の方向に作用すると仮定します。

今回は、四角形物体を「土」と想定して応力の向きを仮定しました。

σ、τ以外の応力が既知とすれば、三角形要素に生じる応力のつりあいより、任意断面に生じる垂直応力σ、せん断力τが算定できます。

2軸方向の応力状態と微小三角形要素

なお、応力の向きを上図のように仮定した理由を下記に示します。

・垂直応力σx、σyの向き　⇒　物体を圧縮する方向とする（圧縮力と仮定）。

「土」は引張強度が期待できない。

ゆえに、引張応力、曲げ応力（引張と圧縮の合成応力）による力の伝達は考えない。

地盤は必ず圧縮力を負担するような設計を行う（引張、曲げが作用する箇所に使わない）。

・任意断面の垂直応力σの向き　⇒　同上

・せん断力τxy（τyx）の向き　⇒　任意の向き

・任意断面のせん断力τの向き　⇒　同上

必ず上図のように、応力の向きを仮定する必要は無いですし、参考書によっては垂直応力の向きが逆になることも多いです（引張力と仮定）。

ただし、応力の組は「物体がつりあうような向き」とします。

なぜなら、力のつりあいを考えるとき物体が静止した状態を考えるからです。

下図のように応力の向きを仮定すると物体は「回転」や「移動」するため、応力の向きの仮定として誤りです。

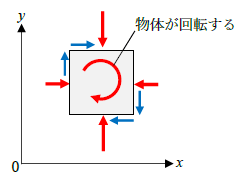
応力の向き

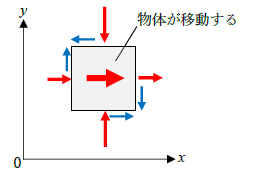
応力の向き2

以降、力のつりあいにより、任意断面の応力を算定しますが、「前述の応力の向きと仮定した場合の式」という点に留意しましょう。

力はベクトルなので「大きさと向きはセット」です。

仮定した応力の向きが変われば、当然、算定結果の符号も逆になります。

ですから「参考書と計算式が合わない」と思う前に、まずは仮定した応力の向きを確認することも大切です。

任意断面の応力の求め方と力のつりあいは？

下図に示す微小三角形要素について、x軸、y軸方向の力のつりあいを考えます。

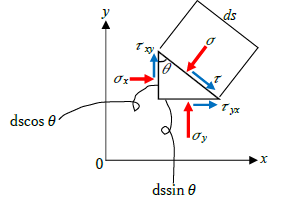
2軸方向の応力状態と力のつりあい

要素は静止した状態であり、すなわち、要素に生じる応力を断面力に変換し、x、y方向ごとに合計すると「0」になります。また、三角形の斜辺の長さはds、角度はθなので

・y方向の長さ　⇒　dscosθ

・x方向の長さ　⇒　dssinθ

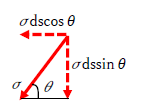
です。次にσ、τをx成分、y成分に分解します。下図より

・σのx成分　⇒　σdscosθ

・σのy成分　⇒　σdssinθ

・τのx成分　⇒　τdssinθ

・τのy成分　⇒　τdscosθ

です。

σとτの分解

以上より

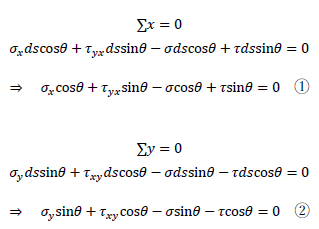
任意断面の応力の求め方と力のつりあい1

です。σx、σy、τxy、τyxは既知なので、上記の２式について連立方程式を解けばσ、τが得られます。さらに、τxy＝τyxが成り立ちます。これをせん断力の共役性といい、説明は省略しますが、詳細は下記が参考になります。

応力の平衡方程式とは？意味・導出と有限要素法・弾性力学への応用（座標軸別の式）

まずσを求めましょう。τの項を消すために式①の各項にcosθを掛け算、式②はsinθを掛け算します。

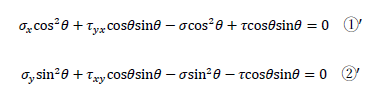
任意断面の応力の求め方と力のつりあい2

上式を足し算してσについて求めると

が得られます。同様の流れでτを求めると（計算過程は省略）

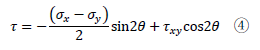
任意断面の応力の求め方と力のつりあい4

になります。式③、④が平面（２次元）の物体の任意断面に生じる垂直応力、せん断応力です。なお、計算過程は省略しましたが、ここまで用いた三角関数の公式を下記に示します。

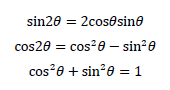
任意断面の応力の求め方と力のつりあい5

応力を表す式としては式③、④で十分ですが、後の議論に繋がる「主応力、主応力面の算定」において、式③を変形しておくと便利なので、より簡単な形で表します。ややテクニックが必要なので計算過程を示します。

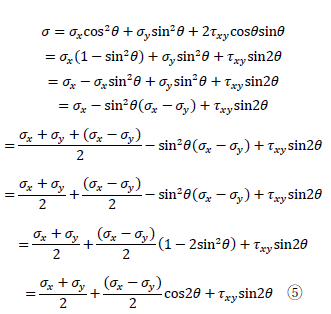
任意断面の応力の求め方と力のつりあい6

一般に、参考書では式⑤が任意断面に生じる垂直応力を表す式として採用されます。平面の物体に生じる主応力の求め方は下記が参考になります。

主応力の求め方は？2次元要素の主応力の導出方法、最大主応力、最小主応力の求め方は？

主応力面とは？せん断応力がゼロの面、主応力度との関係を解説

混同しやすい用語

垂直応力（すいちょくおうりょく・σ）

断面に垂直な方向に作用する応力。

引張または圧縮の力を面積で除したもの。

x軸・y軸方向それぞれに独立に定義され、2軸応力状態ではσxとσyが同時に存在する。

せん断応力（せんだんおうりょく・τ）

断面に平行（接線）方向に作用する応力。

2軸応力状態ではτxyが垂直応力と同時に作用し、任意断面での垂直・せん断応力の大きさはこれら3成分から求まる。

2軸方向に生じる応力を整理した表を示します。

項目	内容	備考
2軸応力の種類	x・y方向の垂直応力＋せん断応力	平面応力状態の基本
主応力面の特徴	せん断応力がゼロになる面	最大・最小の垂直応力が作用する
任意断面の応力算定	微小三角形要素の力のつりあいで導出	モールの応力円の基礎となる概念