1. HOME > 構造力学の基礎 > 主応力の求め方は？2次元要素の主応力の導出方法、最大主応力、最小主応力の求め方は？

主応力の求め方は？2次元要素の主応力の導出方法、最大主応力、最小主応力の求め方は？

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

主応力の求め方はモールの応力円を描くと簡単にわかります。

モールの応力円とは、縦軸にせん断応力、横軸に垂直応力をとり物体に生じる垂直応力、せん断応力の関係を表す円です。

モールの応力円を表す式は、任意断面に生じる垂直応力、せん断応力から導出できます。

今回は、主応力の求め方、2次元要素の主応力の導出方法、最大主応力、最小主応力の求め方について説明します。二軸方向に生じる応力、モールの応力円、主応力面の詳細は下記が参考になります。

2軸方向に生じる応力とは？任意断面の応力の求め方と力のつりあいは？

モールの応力円とは？1分でわかる意味、導出、主応力の求め方は？

主応力面とは？1分でわかる意味、方向、主応力度と主せん断応力度との関係

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

記事を書いた人

ハナダユキヒロ／建築学生が学ぶ「構造力学」

難解な構造力学、建築構造の用語を分かりやすく解説する専門家。高等専門学校在学中から建築学生が学ぶ「構造力学」を運営。その後、国立大学大学院⇒組織設計事務所⇒弊サイト運営に従事している。

著書：「わかる構造力学/工学社」、「わかる構造力学 改訂版/工学社」

LINEで質問したい方はこちら　⇒　【好評】管理人にLINEで質問してみよう

主応力の求め方は？

主応力の求め方は、モールの応力円を描くと簡単にわかります。２次元要素に応力が生じる場合（平面応力状態）の主応力の求め方を下記に示します。

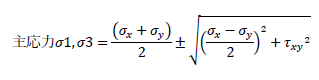
σx、σyはx軸、y軸に生じる垂直応力、τxyはせん断応力です。σ1は主応力の最大値、σ3は主応力の最小値です。

なお、主応力とは物体の任意断面に生じる垂直応力の「極値（最大値、最小値）」です。主応力の最大値を最大主応力、最小値を最小主応力といいます。

主応力について

上式に示す主応力を求める式を導出する前に、主応力の作用する方向、性質を理解しましょう。

２次元（平面）要素には、下図に示すようにｘ軸、ｙ軸方向に垂直応力、せん断応力が生じます。

まずは、平面要素に生じる応力と任意断面に生じる応力とのつりあい関係から、２次元要素の任意断面に生じる垂直応力、せん断応力を求める式を導きましょう。

本記事では導出を省略しますが、導出を知りたい方は下記をご覧ください。

2軸方向に生じる応力とは？任意断面の応力の求め方と力のつりあいは？

２次元要素の任意断面に生じる垂直応力σ、せん断応力τを求める式は下記の通りです。

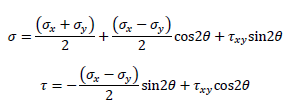
前述したように、主応力とは垂直応力の「極値」です。極値は数学で習ったように「微分して0になる値」です。

忘れている方向けに補足しますが、微分は曲線の一部の傾きを求める操作なので「傾きが０」になるとき、極大値あるいは極小値を表すのです。

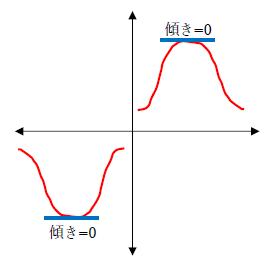
上式のσはθが変数なので、σをθについて微分して（σx、σy、τxyは既知）、0になるときの関係を求めます。

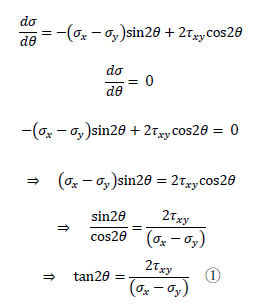
式①より主応力の生じる断面の角度θが得られます（つまり、主応力の生じる面および軸）がわかる）。

なお、同様の操作を行うことで、任意断面に生じるせん断応力の最大値τmaxが算定できます。

式①のtan2θに着目してください。tan2θの角度に90度（π/2）足しても、tanπ＝0なので「tan2(θ+π/2)＝tan2θ」となります。

つまり、tan2θは90度の周期をもっており、式①はtan2θ、tan2(θ+π/2)でも等式を満たします。

前述したように、主応力には最大値と最小値があります。すなわち

・主応力の最大値（最大主応力）と最小値（最小主応力）の軸および作用面は「直交する（90度で交わる）」

ことを意味します。下図をみてください。主応力の作用する面を（主応力面）、主応力の作用方向の軸を「主軸」といいます。

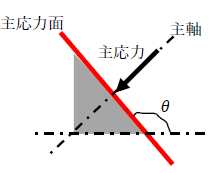
主軸、主応力面の詳細は下記が参考になります。

主応力軸とは？1分でわかる意味、求め方、最大主応力、最小主応力の求め方は？

主応力面とは？1分でわかる意味、方向、主応力度と主せん断応力度との関係

ところで、前述のτを求める式についてτ＝0の関係式を考えます。

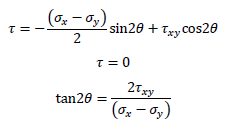
上式は式①と全く同じ式であり、つまり

・主応力の生じる断面ではせん断応力τ＝0となる（せん断応力は生じない）

のです。以上、主応力に関する重要事項を下記に整理しました。

① 主応力とは物体の任意断面に生じる垂直応力の「極値（最大値、最小値）」

② 主応力の最大値（最大主応力）と最小値（最小主応力）の軸および作用面は「直交する（90度で交わる）」

③ 主応力の生じる断面ではせん断応力τ＝0となる（せん断応力は生じない）

2次元要素の主応力の導出方法とモールの応力円

それでは2次元要素の主応力の式を導出します。２軸方向に応力が生じる物体における任意断面の垂直応力、せん断応力は下記の通りでした。

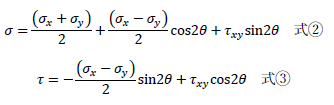
ここで円の方程式を思い出してください。円の方程式は

です。σとτの関係を円の方程式で表すことを目標に式を変形しましょう。式②の右辺を一部移項すると

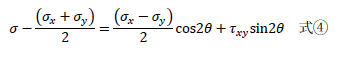
です。次に式④の両辺を二乗、式③の両辺を二乗して足し算します。すると

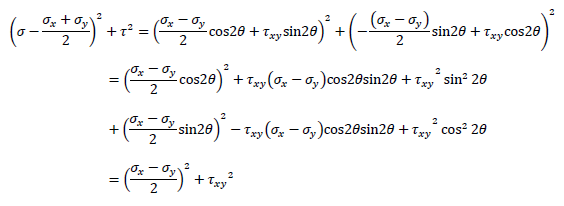
なので

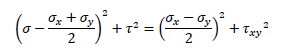
が得られます。さらに右辺を平方根の２乗の形に変形すると

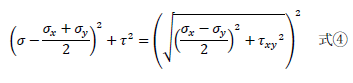
です。上式を円の方程式と見比べると、上式は

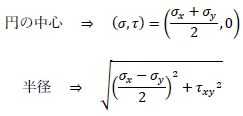
の円の方程式を表すことがわかります。縦軸にせん断応力τ、横軸に垂直応力σをとります。

上式より、円の中心はy軸方向（τ軸方向）に移動しません。すなわち、円の中心とσ軸（x軸）は一致します。

式④で示す円を「モールの応力円」といいます。

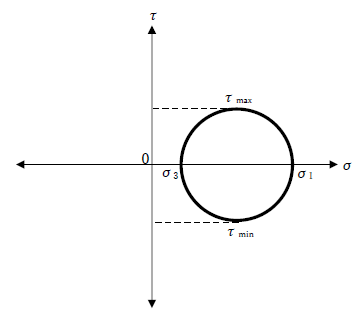
前述の式でも示しましたが、モールの応力円からも主応力の最大値、最小値では「τ＝0」になることが確認できます。式④についてτ＝０を代入してσの値を求めると

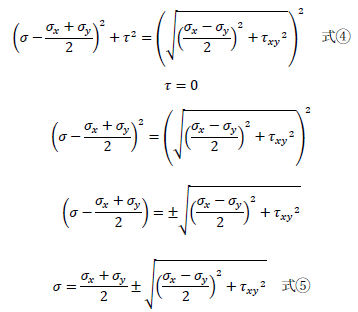
が得られます。上式は前述に示した主応力を求める式と一致しますね。

なお、最大（最小）せん断応力は「円の半径」ですから、最大主応力σ1と最小主応力の差（円の直径）の半分の値なので

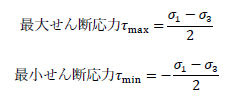
のように算定できます。モールの応力円の詳細は下記も参考になります。

モールの応力円とは？1分でわかる意味、導出、主応力の求め方は？

最大主応力、最小主応力の求め方は？

最大主応力σ1、最小主応力σ3の求め方を下記に示します。なお、構造力学、材料力学の分野では、最大主応力の記号をσ1、最小主応力をσ2とすることが多いです。

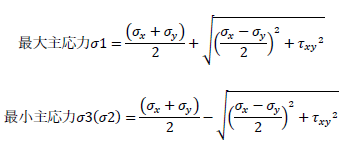
最大主応力、最小主応力の詳細は下記が参考になります。

最大主応力とは？1分でわかる意味、求め方、マイナスの値、圧縮・引張との関係、最小主応力の求め方は？

最大主応力と最小主応力の違いは？1分でわかる意味、求め方、最大主応力と最小主応力のマイナスと引張・圧縮の関係は？

まとめ

今回は主応力の求め方について説明しました。主応力とは、任意断面に生じる垂直応力の最大値および最小値です。

主応力の求め方は、モールの応力円を表す式から簡単に算定できます。まずは二軸方向に応力が生じる場合（平面応力状態）における力のつりあいを理解しましょう。

2軸方向に生じる応力とは？任意断面の応力の求め方と力のつりあいは？

モールの応力円とは？1分でわかる意味、導出、主応力の求め方は？

主軸とは？1分でわかる意味、構造力学との関係、強軸、弱軸との関係

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

▼スポンサーリンク▼

【初回資料が今だけ無料！】1日約13円で情報をアップデート！

有料メルマガを無料で見てみませんか？⇒　忙しい社会人、学生のためのビルディング・アップデート

更新情報

• 当サイトでは、ほぼ毎日、記事更新・追加を行っております。


• 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。


• 新着記事一覧

プロフィール

• 
• 略歴▼
• 名前　ハナダユキヒロ/MITUME lab代表.
• 2010年　弊サイトを開設
• 2010～2017年　国立大学大学院修了
• 2017年12月に当HPが書籍化。
• 「わかる構造力学」
• 2022年4月に「わかる構造力学」の改訂版出版。
• 「わかる構造力学(改訂版)」


• 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。


• 当サイトの目的▼
• 建築学生が学ぶ「構造力学」の目的


• とりあえず10記事▼
• 初めましての方に10記事用意しました


• おすすめ書籍紹介▼
• ハナダユキヒロが建築関連書籍の良書を選びました

建築の本、紹介します。▼

▼【好評！】管理人おすすめ▼

• あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！

同じカテゴリの記事一覧

• 2軸方向に生じる応力とは？任意断面の応力の求め方と力のつりあいは？
• 第一主応力とは？1分でわかる意味、求め方、最大主応力と最小主応力の違い、方向は？
• 最大主応力とは？1分でわかる意味、求め方、マイナスの値、圧縮・引張との関係、最小主応力の求め方は？
• 最大主応力と最小主応力の違いは？1分でわかる意味、求め方、最大主応力と最小主応力のマイナスと引張・圧縮の関係は？
• 主応力差とは？1分でわかる意味、せん断応力との関係、最大主応力の方向、求め方は？
• 主応力軸とは？1分でわかる意味、求め方、最大主応力、最小主応力の求め方は？
• 主せん断応力とは？1分でわかる意味、求め方、導出、方向、主応力との関係は？