1. HOME > 構造力学の基礎 > 最大たわみの公式は？両端支持梁と片持ち梁のたわみの公式の違いと例題

最大たわみの公式は？両端支持梁と片持ち梁のたわみの公式の違いと例題

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

最大たわみδmaxの公式を下記に示します。なお最大たわみとは、梁のたわみ曲線における最大値です。梁に荷重が作用すれば「梁全体がたわむ」のですが、部材の安全性を検討する上では「たわみの最大値」が重要なので最大たわみを単に「たわみ」といいます。なお、最大たわみは、たわみ曲線を導出した上で、数学の極大・極小値の算定方法にならい求めます（後述する）。

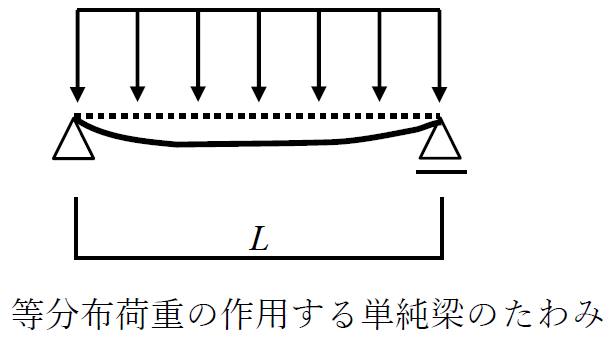
・中央集中荷重　単純梁

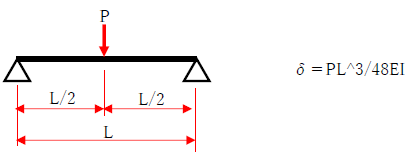
・等分布荷重　単純梁

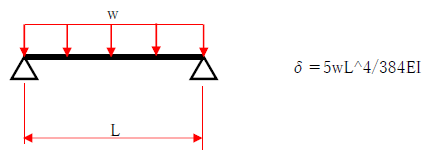
・先端集中荷重　片持ち梁

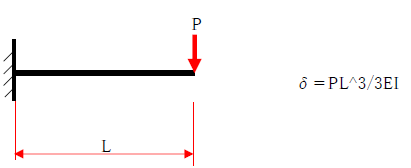
・等分布荷重　片持ち梁

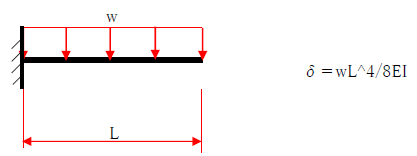
・中央集中荷重　両端固定

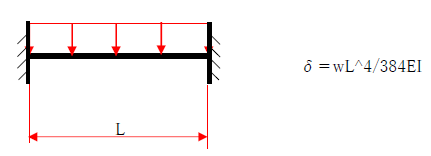
・等分布荷重　両端固定

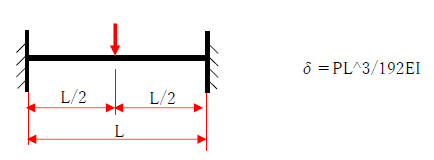
・中央集中荷重　片側ピン片側固定

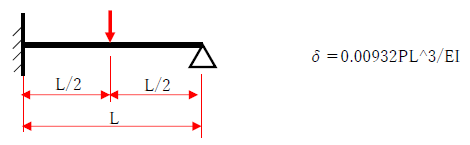
・等分布荷重　片側ピン片側固定

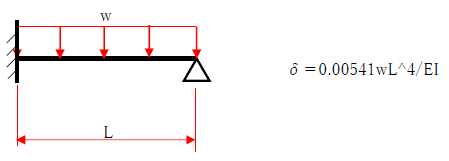
・三角形分布荷重　単純梁

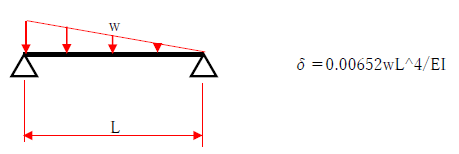
・三角形分布荷重　片持ち梁

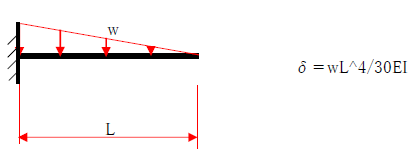
両端支持梁と片持ち梁の最大たわみを比較すると、片持ち梁の最大たわみはかなり大きくなることに気づくでしょう。下記の公式をみると、片持ち梁では分母が8に対して、両端支持梁では約77（＝384/5）であり、荷重w、スパンL、曲げ剛性EIが同様の条件であっても、片持ち梁の方が10倍弱もたわみが大きくなります。よって、構造設計では片持ち梁のたわみ、振動には十分に注意して断面算定を行うべきでしょう。

なお、両端支持梁の最大たわみの生じる位置は等分布荷重であれば梁の「スパンの中央付近」、集中荷重が作用する場合は「荷重の作用位置付近」です。一方、片持ち梁の最大たわみが生じる位置は「片持ち梁の先端部」です。

さて、例題として中央集中荷重が作用する両端支持梁の最大たわみを導出します。この梁に荷重が作用するとき、梁のたわみ曲線は

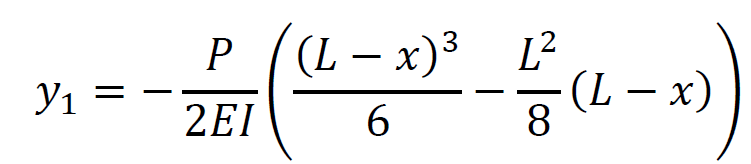
となります。たわみ公式の導出方法は下記をご覧ください。

たわみ公式の導出、片持ち梁、両端支持梁のたわみ公式の導出

最大たわみは、数学の極大値、極小値を求める方法を使います。下記に手順を示します。

１．たわみの式を1回微分する。

２．1回微分して得られた式=0としてxの値を計算する。

y1のたわみを1回微分すると

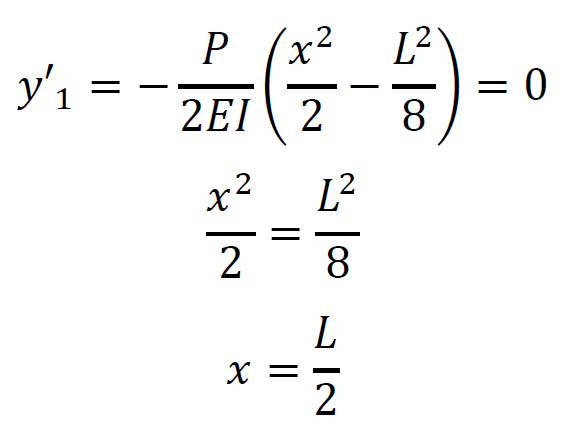
上記よりx=L/2の地点で最大のたわみが発生します。たわみ曲線の式にx=L/2を代入して、たわみの最大値を求めると

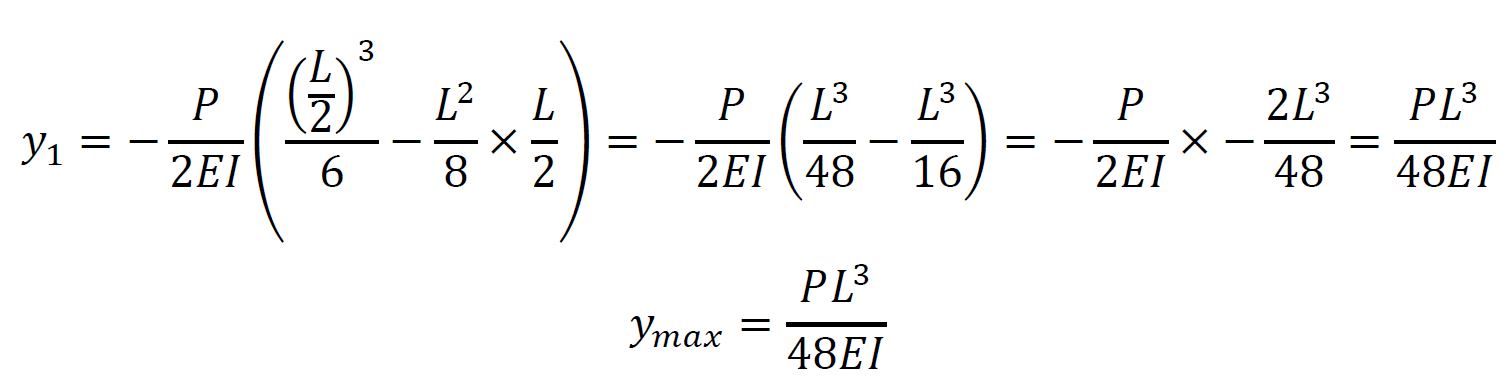
が得られます。

まとめ

今回は、最大たわみの公式を解説しました。最大たわみとは、梁のたわみ曲線における最大値です。梁に荷重が作用すれば「梁全体がたわむ」のですが、部材の安全性を検討する上では「たわみの最大値」が重要なので最大たわみを単に「たわみ」といいます。たわみの公式、たわみの公式の導出方法など下記も勉強しましょう。

たわみの公式は？1分でわかる種類、覚え方、単位、導出

たわみ公式の導出、片持ち梁、両端支持梁のたわみ公式の導出

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

▼スポンサーリンク▼

【初回資料が今だけ無料！】1日約13円で情報をアップデート！

有料メルマガを無料で見てみませんか？⇒　忙しい社会人、学生のためのビルディング・アップデート

更新情報

• 当サイトでは、ほぼ毎日、記事更新・追加を行っております。


• 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。


• 新着記事一覧

プロフィール

• 
• 略歴▼
• 名前　ハナダユキヒロ/MITUME lab代表.
• 2010年　弊サイトを開設
• 2010～2017年　国立大学大学院修了
• 2017年12月に当HPが書籍化。
• 「わかる構造力学」
• 2022年4月に「わかる構造力学」の改訂版出版。
• 「わかる構造力学(改訂版)」


• 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。


• 当サイトの目的▼
• 建築学生が学ぶ「構造力学」の目的


• とりあえず10記事▼
• 初めましての方に10記事用意しました


• おすすめ書籍紹介▼
• ハナダユキヒロが建築関連書籍の良書を選びました

建築の本、紹介します。▼

▼【好評！】管理人おすすめ▼

• あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！

同じカテゴリの記事一覧

• たわみとは？1分でわかる意味、求め方、公式、単位、記号、計算法
• たわみの微分方程式は？導出、単純梁、片持ち梁のたわみの微分方程式と境界条件
• たわみの記号は？1分でわかる記号と意味、読み方、書き方、単位、ヤング率の記号
• たわみの単位は？記号、公式、例題と計算は？
• たわみ角とは？1分でわかる意味、公式、単位、例題から学ぶ計算法
• 梁のたわみを求める方法
• 単純梁のたわみは？1分でわかる求め方、公式、計算と例題
• 片持ち梁のたわみを求める方法
• 集中荷重が途中に作用する片持ち梁のたわみは？先端荷重が作用する片持ち梁のたわみは？
• 両端支持のたわみ計算は？1分でわかる計算、公式、両端固定梁のたわみ