1. HOME > 構造力学の基礎 > 支点反力の公式と計算

支点反力の公式と計算

支点反力の公式を下図に示します。下図の通り、支点反力の公式は、荷重条件、支持条件に応じて変わります。

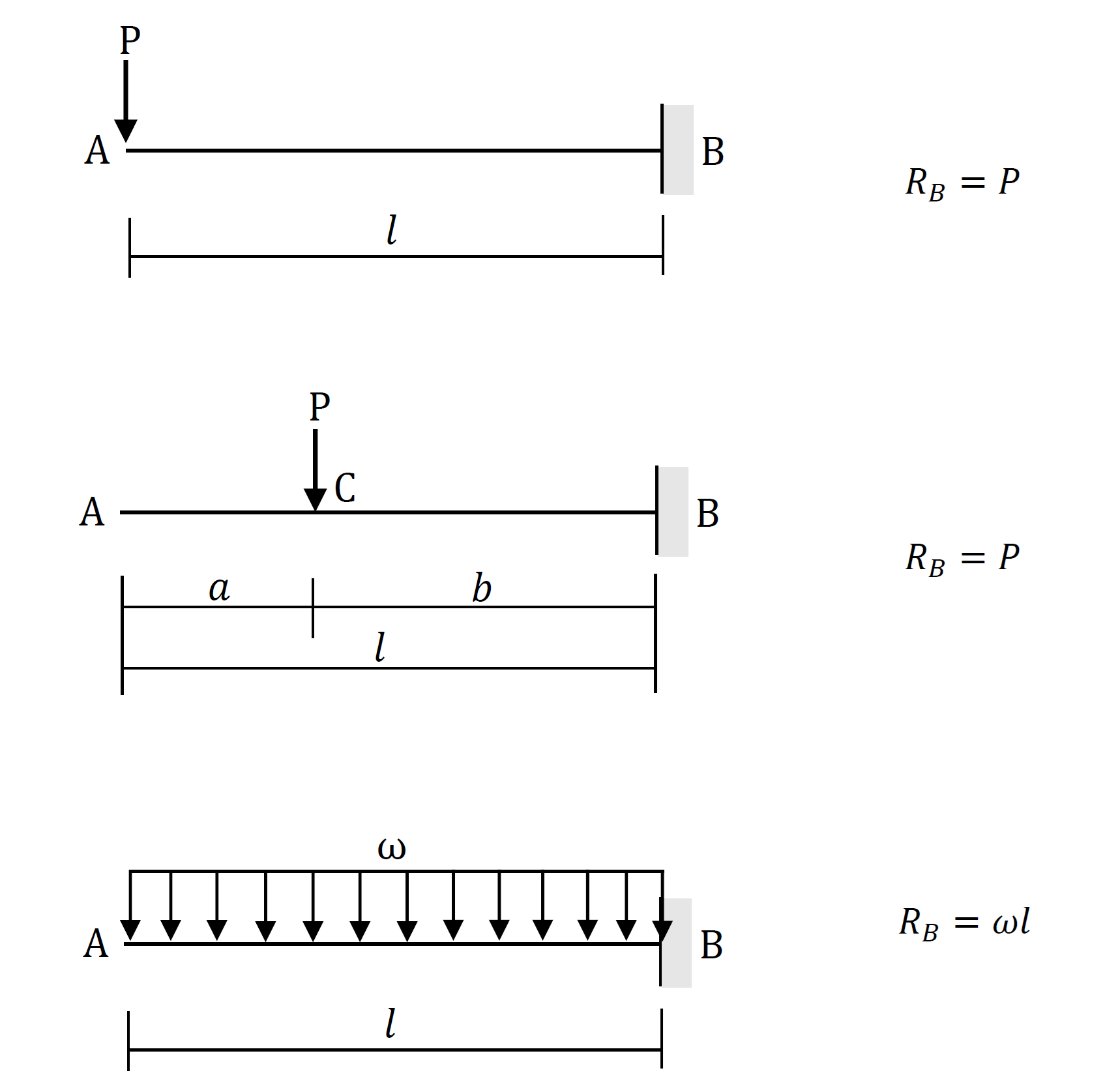
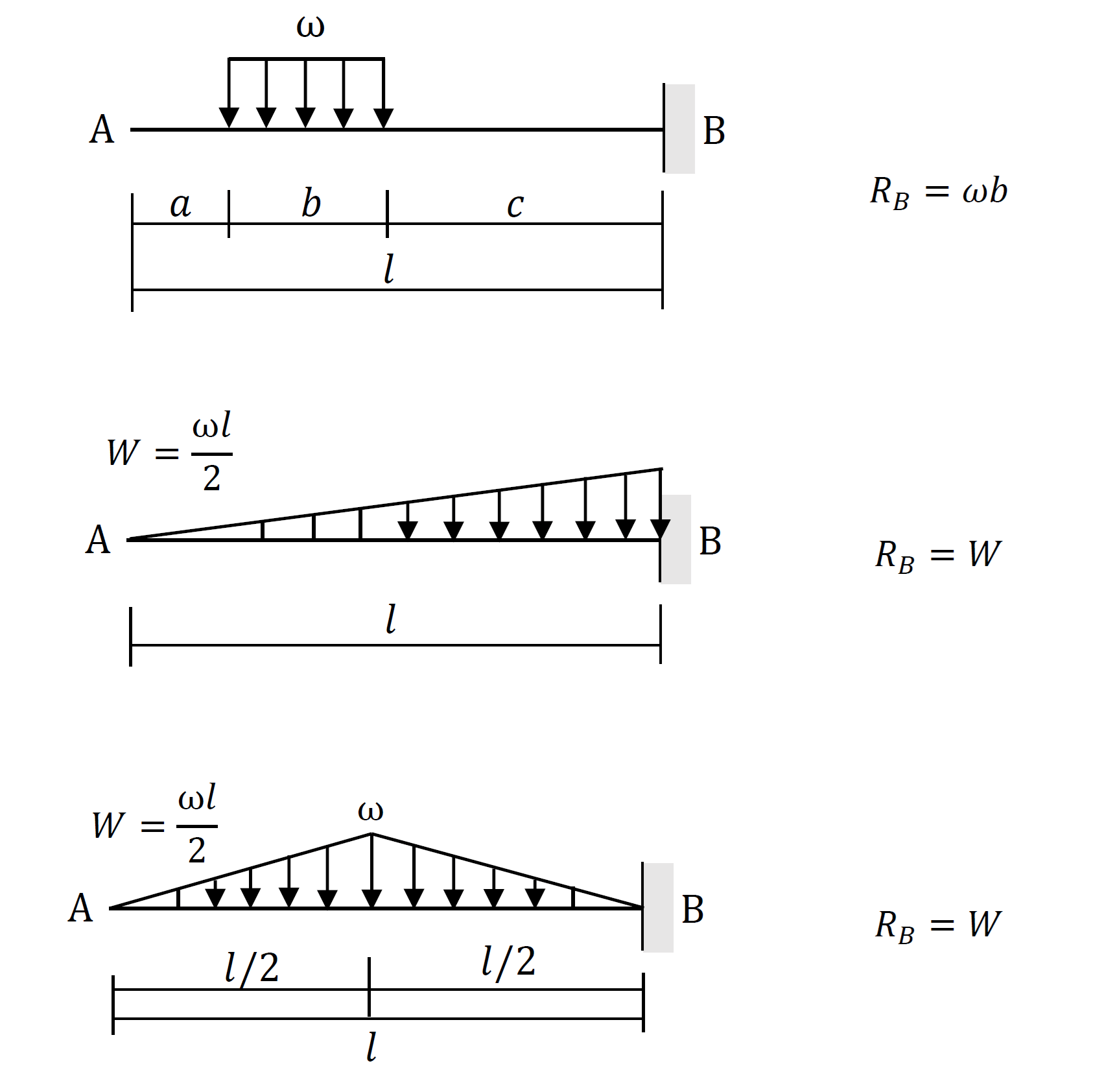
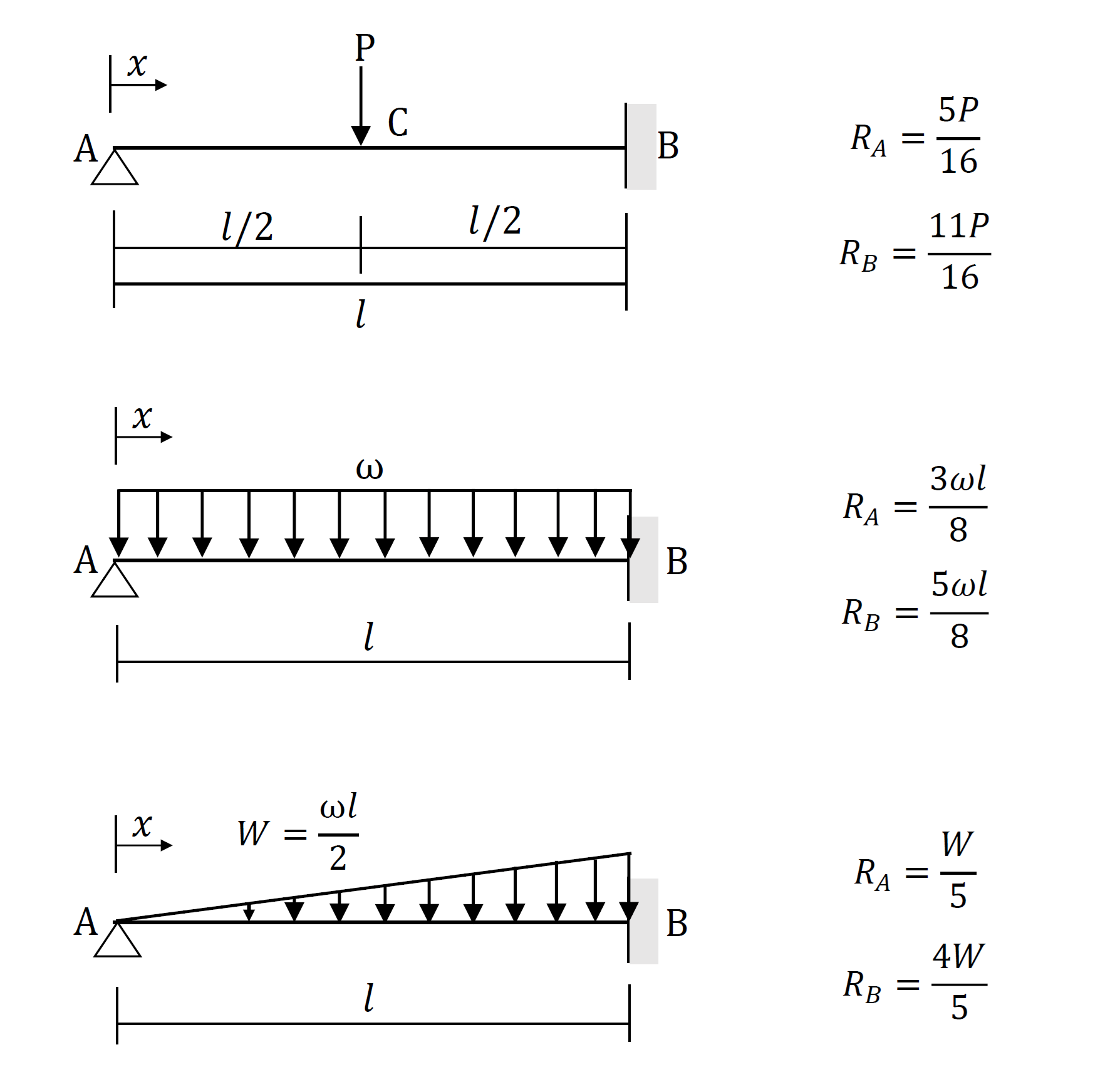
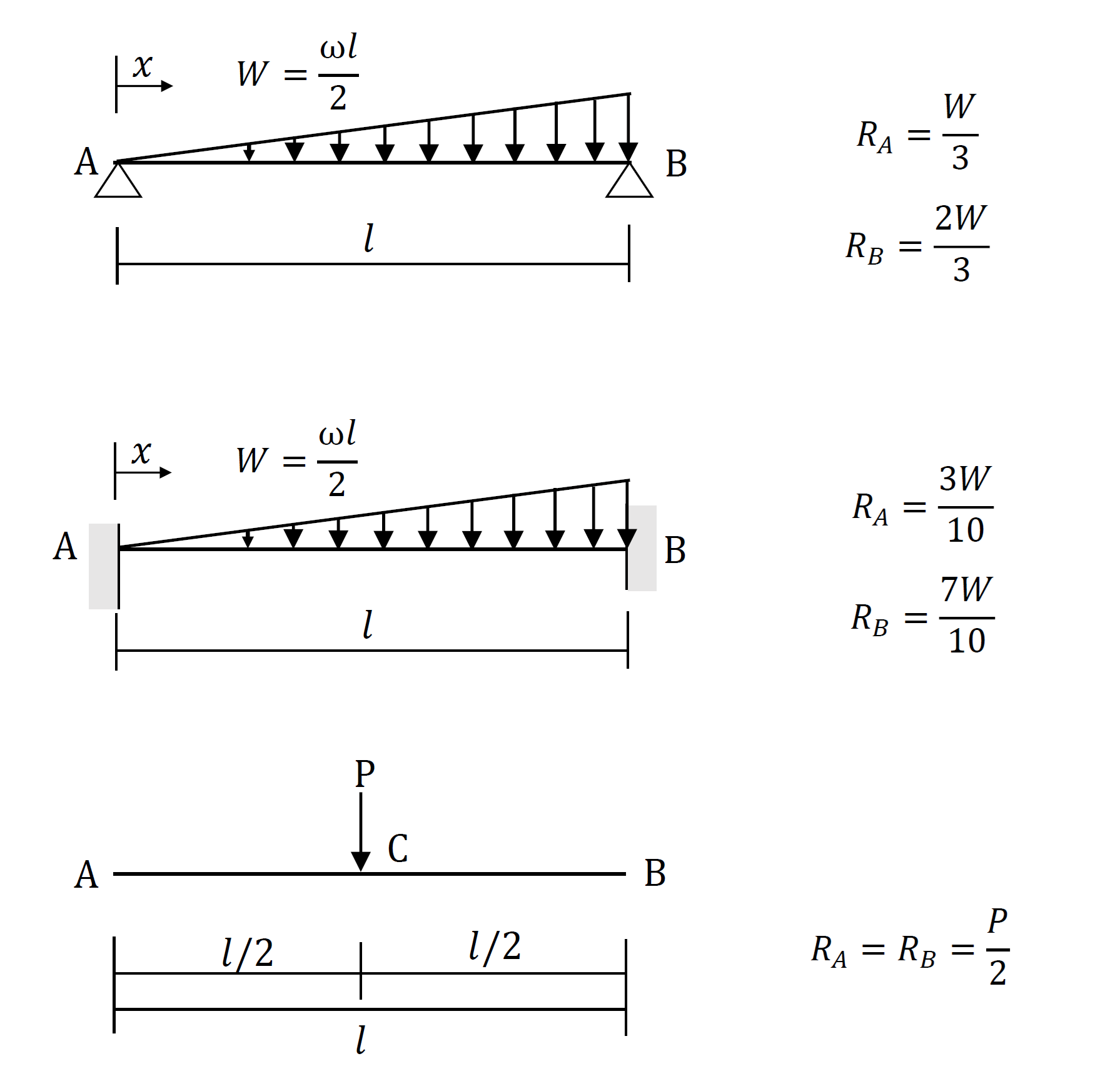
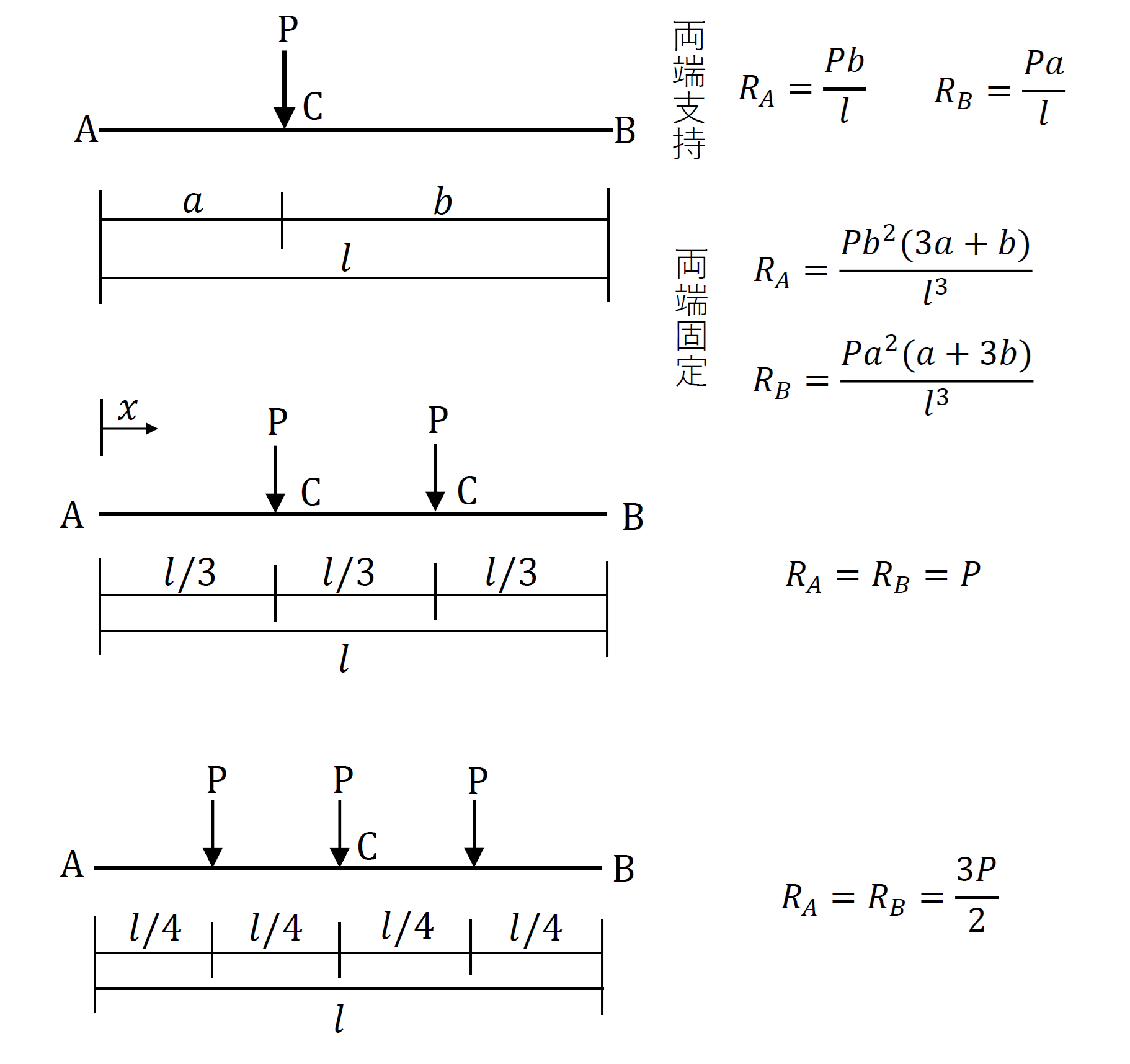
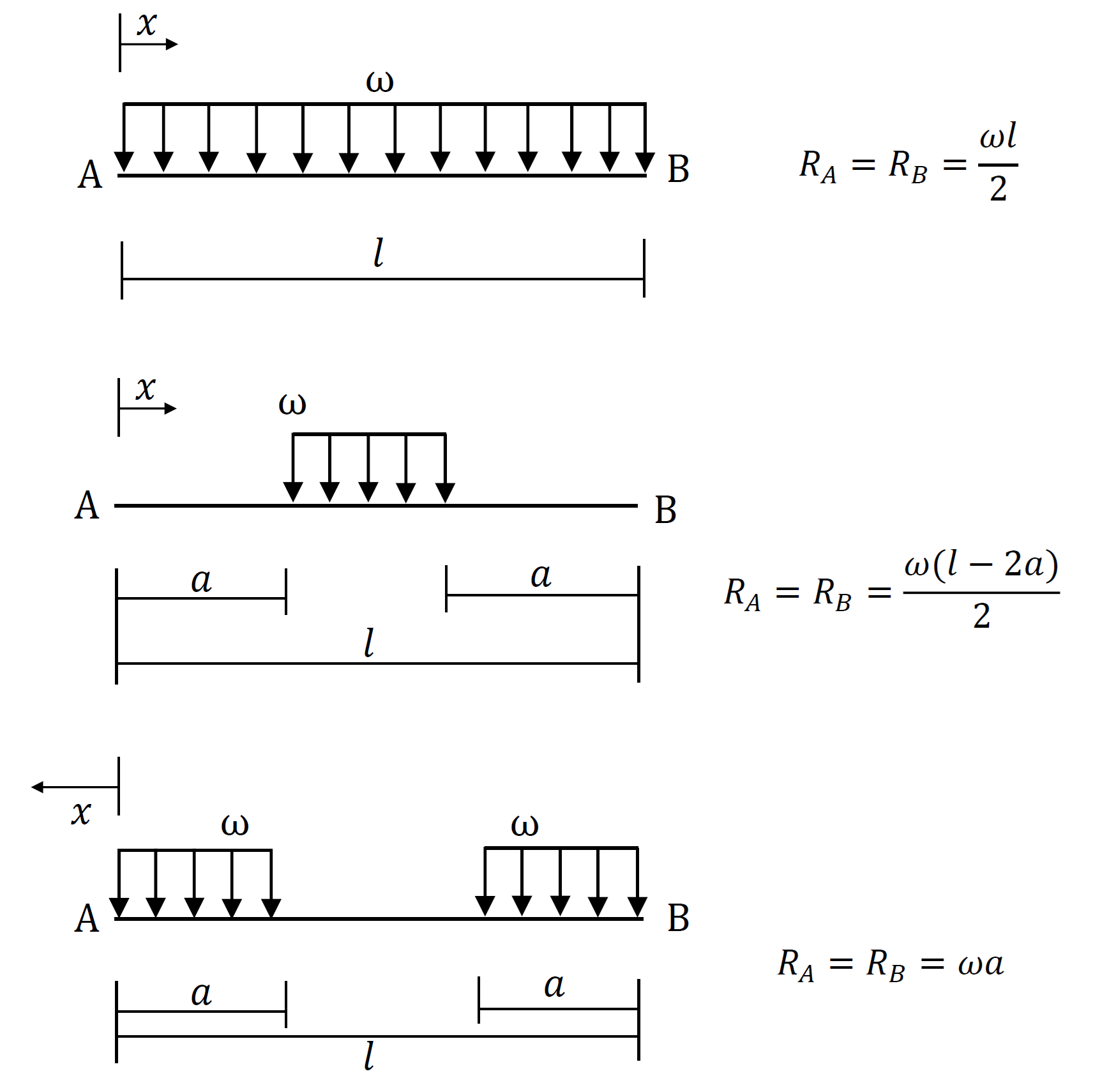
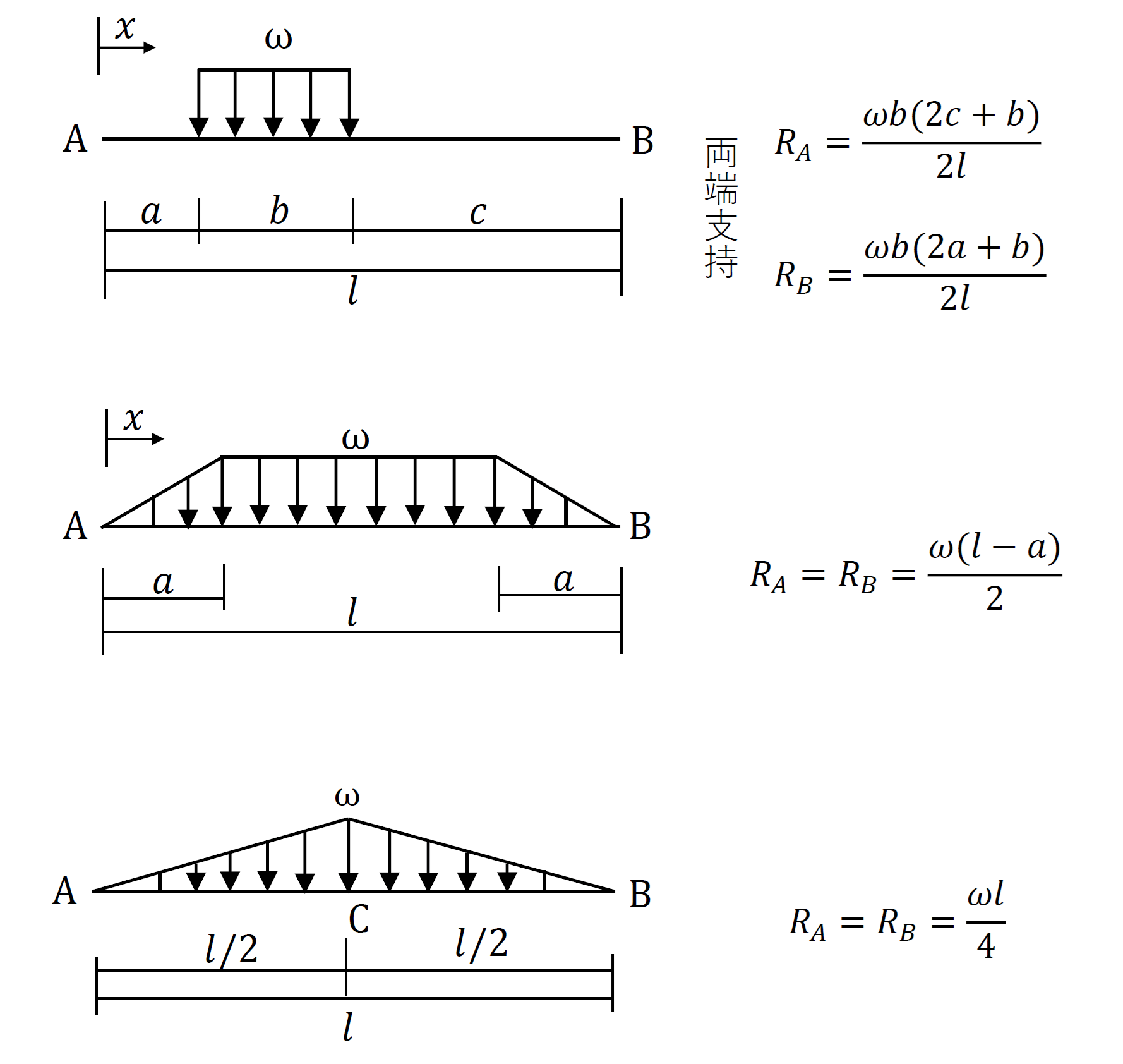
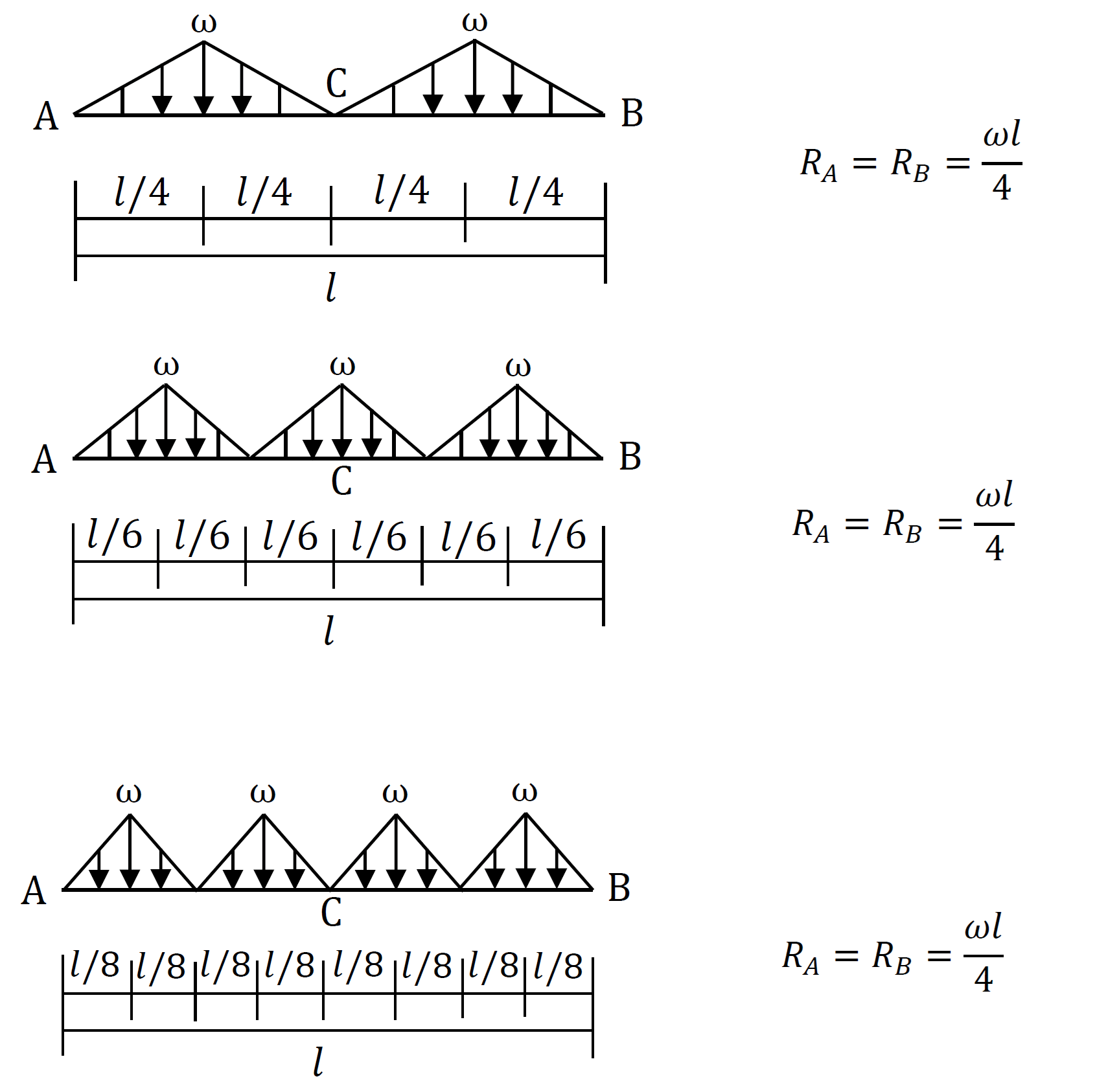
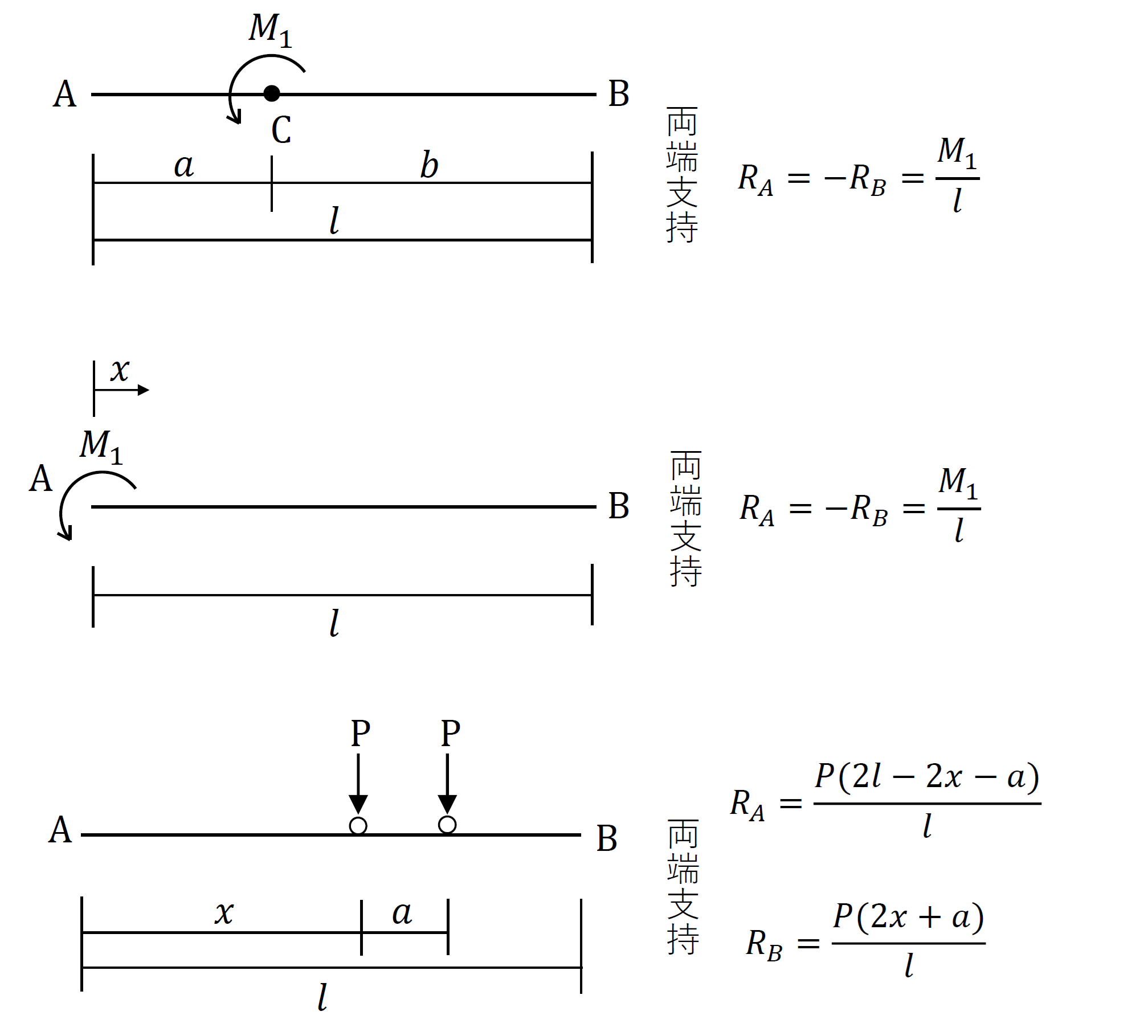
上図の支点反力の公式は、全て静定構造の梁の値なので、力のつり合い（ΣV=0、ΣH=0、ΣM=0）を組み立てて算定できます。簡単な荷重、支持条件の梁を例題に、力のつり合いから支点反力を算定します。

反力の求め方は簡単です。静止する物体における全ての力はつりあいます。つまり、外力と反力についてΣH=0、ΣV=0、ΣM=0の関係から反力を求めれば良いのです。なお、下図に示すローラー支点とピン支点からなる梁を単純梁といいます。

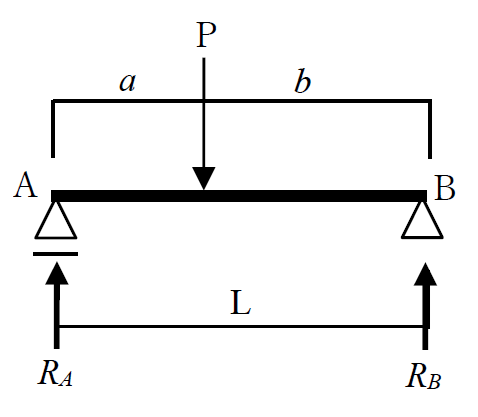
水平方向の力のつり合い

力のつりあいを考えるとき、下図のように反力の向きを仮定して図示すると分かりやすいです。水平反力は右向き、鉛直反力は上向きの力として仮定します。また、力に符号をつけて向きを表します。本書では「右・上向きの力を正、左・下向きの力を負」と考えます。どの向きを正とするかは自由ですが、正値とした方向の逆方向は必ず負値となるように定義します。下添え字のA、Bは単なる目印ですので1、2でも構いません。

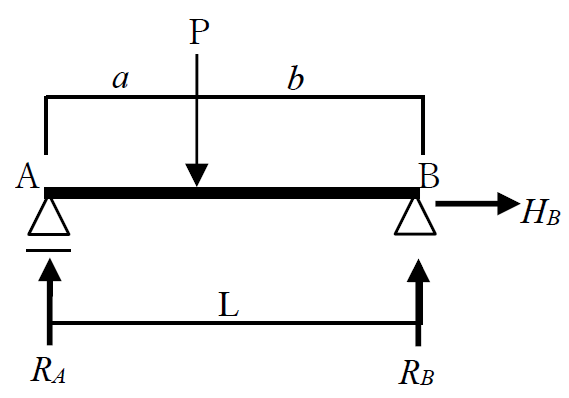
水平力は仮定した反力のみなので、

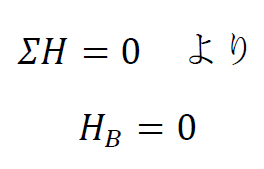
です。外力が作用していないので、当然、反力もありません。

鉛直方向の力のつり合い

次に、鉛直方向の力のつり合いを考えます。

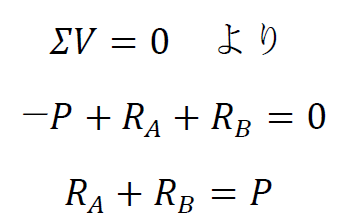
モーメントのつり合い

ここが一番の難関ですね。モーメントのつり合いを考えます。A、B点はローラー支点、ピン支点なのでモーメントは生じません。よって、A(B)点でのモーメントのつり合いはゼロになります。

A点における全てのモーメントを求めます。回転方向が時計回りの値を正とすると、梁中央に作用する力Pによるモーメントは

です。Ｂ支点には仮定した反力RBが上向きの力で作用します。RBはA点を軸に反時計回りの回転を起こすので

です。これらのモーメントの合計は0になるので

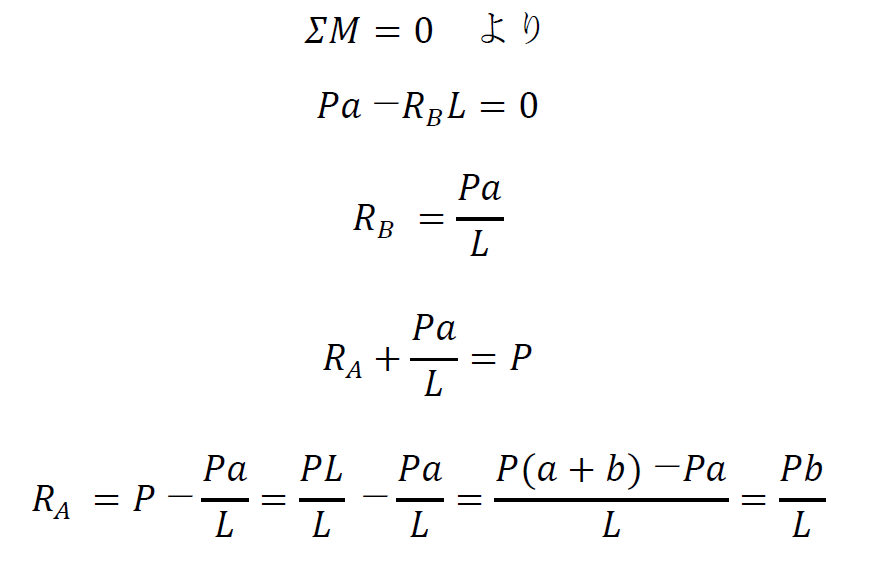
となります。

RA、RB共に正の値です。つまり、仮定した反力の方向が正しいことを意味します。仮に反力が負の値であれば、仮定した反力の向きと反対向きに反力が作用しています。

ところで、Ａ点を中心としたモーメントのつりあいを考えたので RＡに関するモーメントは0です。RＡはＡ点に作用しておりA点を中心に考えると距離は0です。M＝力×距離＝RＡ×０＝０です。

あとは荷重条件、支持条件の変化に応じて計算が変わるだけです。荷重、支持条件の種類は下記が参考になります。

等分布荷重とは？集中荷重との違いや使い方について

支点とは？わかりやすい意味【図解】

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

▼スポンサーリンク▼

▼【好評！】管理人おすすめ▼

• あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！

▼用語の意味知らなくて大丈夫？▼

▼同じカテゴリの記事一覧▼

• 反力ってなに？反力の求め方と支点反力
• 反力の単位は？1分でわかる単位、意味、読み方、記号
• 水平反力とは？1分でわかる意味、求め方（計算方法）、符号、記号
• 支点反力とは？どういう意味、求め方
• 床反力の読み方は？1分でわかる読み方、意味、床反力の計算、鉛直・水平方向の関係
• モーメント反力とは？正負の値、求め方は？
• 外的安定とは？1分でわかる意味、外的不安定、内的安定との関係
• 支点を理解すれば構造力学が分かる
• 固定支点とは？1分でわかる意味、反力、モーメントとの関係、ピン支点、ローラー支点との違い
• ピン支点とは？1分でわかる意味、モーメント反力との関係、ローラー支点、固定支点との違い

▼カテゴリ一覧▼

• 建築物と構造力学の関係(まずは、苦手な勉強の進め方から)
• モデル化を学ぶ(まずは、構造物のモデル化から)
• 静定構造物の解き方を学ぶ(まずは、静定構造物に関する基礎用語から)
• 断面の性質を学ぶ(まずは、断面図形に関する基礎用語から)
• 梁のたわみを学ぶ(まずは、梁のたわみと基礎用語から)

▼他の勉強がしたい方はこちら▼

• 構造力学の基礎
• 構造計算の基礎
• 鋼構造（鉄骨構造）の基礎
• 鉄筋コンクリート造の基礎
• 基礎構造
• 数学の基礎
• 水理学の基礎
• 材料力学の基礎
• 構造力学の応用
• 耐震設計の基礎
• 有限要素法の基礎
• 一級・二級建築士の勉強
• 建築学生向け就職、学業情報
• 建築構造に関する一般向け情報
• 計算プログラムから構造力学を学ぶ

【初回資料が今だけ無料！】1日約13円で情報をアップデート！

有料メルマガを無料で見てみませんか？⇒　忙しい社会人、学生のためのビルディング・アップデート

更新情報

• 当サイトでは、ほぼ毎日、記事更新・追加を行っております。


• 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。


• 新着記事一覧

プロフィール

• 
• 略歴▼
• 名前　ハナダユキヒロ/MITUME lab代表.
• 2010年　弊サイトを開設
• 2010～2017年　国立大学大学院修了
• 2017年12月に当HPが書籍化。
• 「わかる構造力学」
• 2022年4月に「わかる構造力学」の改訂版出版。
• 「わかる構造力学(改訂版)」


• 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。


• 当サイトの目的▼
• 建築学生が学ぶ「構造力学」の目的


• とりあえず10記事▼
• 初めましての方に10記事用意しました


• おすすめ書籍紹介▼
• ハナダユキヒロが建築関連書籍の良書を選びました

建築の本、紹介します。▼

▼【好評！】管理人おすすめ▼

• あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！

同じカテゴリの記事一覧

• 反力ってなに？反力の求め方と支点反力
• 反力の単位は？1分でわかる単位、意味、読み方、記号
• 水平反力とは？1分でわかる意味、求め方（計算方法）、符号、記号
• 支点反力とは？どういう意味、求め方
• 床反力の読み方は？1分でわかる読み方、意味、床反力の計算、鉛直・水平方向の関係
• モーメント反力とは？正負の値、求め方は？
• 外的安定とは？1分でわかる意味、外的不安定、内的安定との関係
• 支点を理解すれば構造力学が分かる
• 固定支点とは？1分でわかる意味、反力、モーメントとの関係、ピン支点、ローラー支点との違い
• ピン支点とは？1分でわかる意味、モーメント反力との関係、ローラー支点、固定支点との違い