断面二次モーメントと曲げモーメントの関係は？断面二次モーメントが大きいとどうなる？
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
断面二次モーメントIと曲げモーメントMの関係を下記に示します。下式の通り、曲げモーメントMを断面二次モーメントIで割り算し、縁端距離y1(y2)を掛け算すると、曲げ応力度σが得られます。
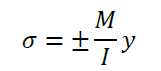
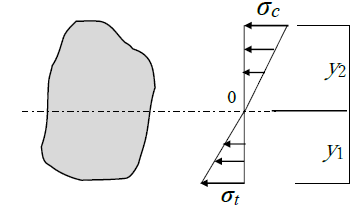
上式の関係より、断面二次モーメントIが大きいほど断面に生じる曲げ応力度σは小さくなります。これを単純に表現ですると「断面二次モーメントを大きくすると、曲げに強くなる」ということですが、何が、どう強いのか定量的に解説しましょう。
さて曲げモーメントに対して部材が問題ないかどうかは、許容応力度と部材に生じる曲げ応力度を比較して「許容応力度＞曲げ応力度」を確認します。
たとえば、ある部材の長期許容応力度が156N/mm2、断面に生じる曲げ応力度が150N/mm2とします。この部材の曲げモーメントに対する余裕は約4％（≒1－150/156）ほどしかなく、少しの荷重増加が起きれば、曲げ応力度が許容応力度を超えてしまい安全性を損ないます。そこで、部材の断面二次モーメントIを大きくするのです。たとえば、Iを1割ほど大きくすれば、曲げ応力度は約136.3N/mm2（≒150/1.1）となり、部材の曲げモーメントに対する余裕は約13％（≒1－136/156）に増えます。
つまり、Iを大きくして曲げ応力度が小さくなることにより、部材断面の曲げモーメントに対する負担が減る（余裕が増える）のです。
さらに、断面二次モーメントを大きくすると「たわみ」が小さくなります。たわみの計算式は荷重条件、支持条件によって様々ですが、最も簡単なたわみの公式を下記に示します。
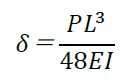
上式より、分母に断面二次モーメントIがあるため、Iが大きくなるほど、たわみδは小さくなります。断面二次モーメントを大きくすれば、部材断面の曲げモーメントに対する負担が減り、たわみも小さくなります。これを一言でいってしまえば、Iを大きくすると「部材はかたくなり、曲げにくくなる」ということです。
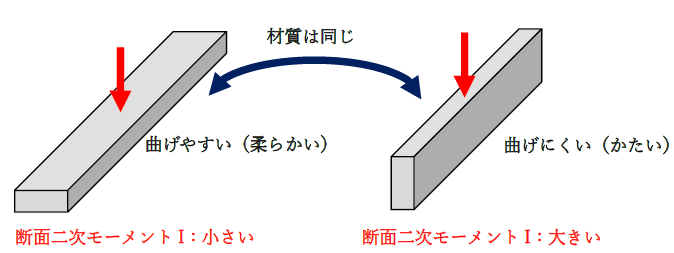
では、どうすれば断面二次モーメントを大きくできるのでしょうか。長方形の断面二次モーメントの公式を下記に示します。bは長方形の幅、hは高さです。よって、Iを効率的に大きくしたければIはhの三乗に比例するので、断面の高さhを増やすべきです。
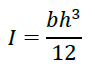
まとめ
今回は、断面二次モーメントと曲げモーメントの関係について説明しました。断面二次モーメントを大きくするほど曲げ応力度は小さくなり、部材断面の曲げモーメントに対する負担が減るといえます。断面二次モーメント、曲げモーメントの詳細は下記が参考になります。
断面二次モーメントとは？1分でわかる意味、計算式、h形鋼、公式、たわみとの関係
曲げモーメントとは？わかりやすい意味、正負の考え方、記号と単位、曲げモーメントからせん断力を求める方法、公式、計算例は？
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
▼スポンサーリンク▼
▼【好評！】管理人おすすめ▼
- あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！
▼用語の意味知らなくて大丈夫？▼
▼同じカテゴリの記事一覧▼
- 断面二次モーメントと断面係数の違い、関係は？断面係数から断面二次モーメントの変換方法は？
- 断面二次モーメントの導出方法は？式の意味と考え方、慣性モーメントとの関係
- 断面二次モーメントを積分で求める理由は？ｈ型の断面二次モーメントを求める計算は？
- 断面二次モーメントのIxとIyの違いは？1分でわかる意味、使い方、計算方法は？
- 断面二次モーメントと図心の関係は？3分でわかる意味と計算、図心を通らない断面二次モーメントの求め方
- 断面二次モーメントとたわみの関係は？1分でわかる意味、計算式、剛性との関係
- 平行軸の定理と断面二次モーメントの関係は？導出方法、図心と通らない場合の断面二次モーメントの求め方
- 曲げ剛性と断面二次モーメントの関係は？断面2次モーメントを大きくするにはどうしたらいい？
- 座屈（棒の座屈）と断面二次モーメントの関係は？1分でわかる意味、座屈荷重の計算式、断面二次半径との関係は？
▼カテゴリ一覧▼
- 建築物と構造力学の関係(まずは、苦手な勉強の進め方から)
- モデル化を学ぶ(まずは、構造物のモデル化から)
- 静定構造物の解き方を学ぶ(まずは、静定構造物に関する基礎用語から)
- 断面の性質を学ぶ(まずは、断面図形に関する基礎用語から)
- 梁のたわみを学ぶ(まずは、梁のたわみと基礎用語から)
▼他の勉強がしたい方はこちら▼
【好評】LINEで質問！
管理人に質問してみる？
わかる1級建築士の計算問題解説書
【初回資料が今だけ無料！】1日約13円で情報をアップデート！
有料メルマガを無料で見てみませんか？⇒ 忙しい社会人、学生のためのビルディング・アップデート
わかる2級建築士の計算問題解説書！
【30%OFF】一級建築士対策も◎！構造がわかるお得な用語集
更新情報
- 当サイトでは、ほぼ毎日、記事更新・追加を行っております。
- 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。
- 新着記事一覧
プロフィール
- 略歴▼
- 名前 ハナダユキヒロ/MITUME lab代表.
- 2010年 弊サイトを開設
- 2010～2017年 国立大学大学院修了
- 2017年12月に当HPが書籍化。
- 「わかる構造力学」
- 2022年4月に「わかる構造力学」の改訂版出版。
- 「わかる構造力学(改訂版)」
- 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。
- 当サイトの目的▼
- 建築学生が学ぶ「構造力学」の目的
- とりあえず10記事▼
- 初めましての方に10記事用意しました
- おすすめ書籍紹介▼
- ハナダユキヒロが建築関連書籍の良書を選びました
建築の本、紹介します。▼
▼【好評！】管理人おすすめ▼
- あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！
同じカテゴリの記事一覧
- 断面二次モーメントと断面係数の違い、関係は？断面係数から断面二次モーメントの変換方法は？
- 断面二次モーメントの導出方法は？式の意味と考え方、慣性モーメントとの関係
- 断面二次モーメントを積分で求める理由は？ｈ型の断面二次モーメントを求める計算は？
- 断面二次モーメントのIxとIyの違いは？1分でわかる意味、使い方、計算方法は？
- 断面二次モーメントと図心の関係は？3分でわかる意味と計算、図心を通らない断面二次モーメントの求め方
- 断面二次モーメントとたわみの関係は？1分でわかる意味、計算式、剛性との関係
- 平行軸の定理と断面二次モーメントの関係は？導出方法、図心と通らない場合の断面二次モーメントの求め方
- 曲げ剛性と断面二次モーメントの関係は？断面2次モーメントを大きくするにはどうしたらいい？
- 座屈（棒の座屈）と断面二次モーメントの関係は？1分でわかる意味、座屈荷重の計算式、断面二次半径との関係は？
- HOME > 構造力学の基礎 > 断面二次モーメントと曲げモーメントの関係は？断面二次モーメントが大きいとどうなる？
- 1級の過去問(計算)解説
- 限定メルマガ
- わかる建築構造の用語集・図解集
- 1頁10円！PDF版の学習記事