HOME > 構造力学の基礎 > 断面二次モーメントと断面係数の違い、関係は？断面係数から断面二次モーメントの変換方法は？

【無料お試しキャンペーン中！】1級・2級建築士試験の構造の疑問を気軽に相談　初心者でもわかる！1級・2級建築士試験(構造)相談カフェ
管理人が業界分析！1日13円で建築業界がわかるLINE配信！　⇒　まずはリンクをクリックして友だち追加！

断面二次モーメントと断面係数の違い、関係は？断面係数から断面二次モーメントの変換方法は？

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

断面二次モーメントは、部材断面を曲げる力に対する抵抗性すなわち「曲げにくさ（曲げやすさ）」を表す値です。また、断面係数は断面二次モーメントを断面の図心より上下縁までの距離で除した値と定義されます。さらに「曲げ応力度＝曲げモーメント÷断面係数」で算定できるので、曲げ応力度は断面係数（または断面係数は曲げ応力度）に反比例します。

なお、断面係数は「部材の曲げに対する強さ、どの程度強いか表す値」と説明する記事もありますが「強さ」は曖昧かつ不正確な表現と考えます。今回は、断面二次モーメントと断面係数の違い、関係、断面係数から断面二次モーメントの変換方法について説明します。断面二次モーメント、断面係数の詳細は下記をご覧ください。

断面二次モーメントとは？1分でわかる意味、計算式、h形鋼、公式、たわみとの関係

断面係数とは

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

断面二次モーメントと断面係数の違い、関係は？

断面二次モーメントと断面係数の違いを下記に示します。

・断面二次モーメント　⇒　部材断面を曲げる力に対する抵抗性、曲げにくさ（曲げやすさ、あるいは、かたさ）を表す値

・断面係数　⇒　断面二次モーメントを断面の図心より上下縁までの距離で除した値と定義される

上記より、断面係数は「断面二次モーメントを元に得られる値」であり、基本的には、断面二次モーメントおよび断面係数共に「部材断面を曲げる力に対する抵抗性」を表します。ただし、後述しますが断面係数は「梁の曲げ応力度を求める式」から定義される値です。

なお、断面係数は「部材の曲げに対する強さ、どの程度強いか表す値」と説明する記事もありますが、ここでの「強さ、強い」は、曖昧かつ不正確な表現と考えます。

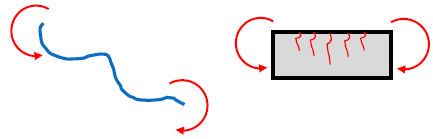
「強さ」の意味を考えてください。「強さ」は物理的に何を意味するのでしょうか。剛性が高い、強度が大きい、あるいはその両者を意味するのですか？下図のように、簡単に曲げられるが「曲げる力では切れない糸」と、簡単に曲がらないが「曲げる力で壊れてしまうコンクリート」のどちらが「強い」のでしょうか。当然、判断できません。「強い」という用語は、物理的に正確な意味を持たないからです。

断面二次モーメントと断面係数の違い1

次に、断面二次モーメントと断面係数の違いを深く理解するために、それぞれの導き方を詳しく解説します。

まず、断面二次モーメントは、物理学でいう「慣性モーメント（物体の回転のしやすさを表す値）」について、断面の回転のしやすさに置き換えて導くのです。

下図に示すように、点Oを中心に物体を回すことを考えます。物体A、Bのどちらが回しやすいか考えましょう。

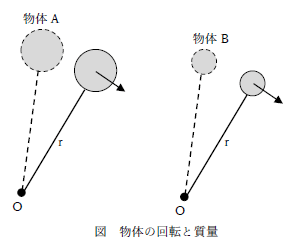
断面二次モーメントと断面係数の違い2

直感的に質量の大きい物体Aの方が回しにくい、と感じる方が多いと思います。では下図に示す条件はどうでしょうか。物体の質量は同じですが、回転中心から物体の中心までの距離が違います。

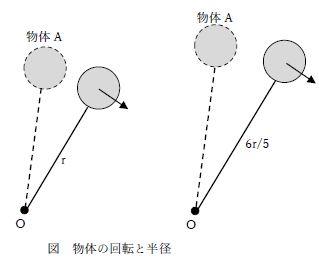
断面二次モーメントと断面係数の違い3

上図の場合、距離の長い方が回しにくいと感じたはずです。

さて、物体の質量をm、回転中心から物体の中心までの距離（回転半径）をrとするとき、mとrの２乗の積を慣性モーメントといいます。

慣性モーメントを、断面の回転のしやすさに置き換えて考えましょう。慣性モーメントはI＝mr2で求められます。断面について考えるのですから、m(＝ρAL)の密度ρと長さLを無視すれば、質量mは断面積Ａに置き換えできます。

また、回転中心を任意のx軸、y軸と考え、軸から断面の図心までの距離をx、yとすれば、x軸、y軸まわりの回転のしやすさ、すなわち曲げやすさを表す下式が得られます。

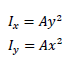
断面二次モーメントと断面係数の違い4

上式より、Iはx、yの２乗に比例するので、断面積の大きさよりも軸から図心までの距離を離すほうが、効率的に曲げにくい断面とできることがわかります。次に、回転軸を図心として任意断面の曲げやすさを考えます。

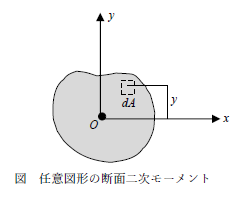
断面二次モーメントと断面係数の違い5

任意断面の微小断面積をdAとし、x軸から微小断面の図心までの距離をyとします。このとき微小断面の曲げやすさは下式で表します。

全断面の曲げやすさを求めるには、全断面における上式の総和すなわち積分すればよいので

が得られます。上式をx軸まわりの断面二次モーメントといいます。同様にy軸まわりの断面二次モーメントは

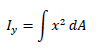
断面二次モーメントと断面係数の違い8

となります。

断面二次モーメントとは？1分でわかる意味、計算式、h形鋼、公式、たわみとの関係

以上より、断面二次モーメントは「断面の回転のしにくさ（曲げにくさ）」だとわかります。次に、断面係数の定義式を導きます。前述したように、断面係数は梁の曲げ応力度を求める式から定義されます。下式に、梁の曲げ応力度の算定式を示します。なお、導出方法は下記をご覧ください。

梁の曲げ応力度と誘導方法

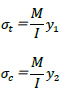
断面二次モーメントと断面係数の違い9

上式についてI/y＝Zと置き換えれば

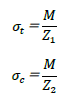
断面二次モーメントと断面係数の違い10

となりますね。このZを断面係数というのです。つまり断面係数Zは

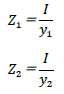
断面二次モーメントと断面係数の違い11

で求めます。上式のように、断面係数は、１つの断面に対して２通りの値があります。ただし、図心から上下縁までの距離が等しければ（図心が断面の真ん中にあれば）、Z1=Z2です。前述のように、断面係数は断面二次モーメントを元に定義される値であり、特別に部材の曲げに対する強さを表す訳では無いのです。

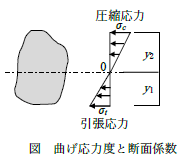
曲げ応力度と断面係数

さらに、下式より、「曲げ応力度＝曲げモーメント÷断面係数」で算定できるので、曲げ応力度は断面係数に反比例します。

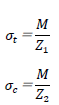
断面二次モーメントと断面係数の違い12

上式を断面係数Zについて解けば「断面係数＝曲げモーメント÷曲げ応力度」なので、断面係数は曲げ応力度に反比例します。

断面係数とは

断面係数から断面二次モーメントの変換方法は？

断面係数の値に、断面の図心から上下縁までの距離yを掛け算すれば断面二次モーメントに変換できます。計算式を下記に示します。

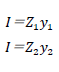
断面係数から断面二次モーメントの変換方法

まとめ

今回は、断面二次モーメントと断面係数の違いについて説明しました。断面二次モーメントは、部材断面を曲げる力に対する抵抗性（曲げにくさ、曲げやすさ）を表します。また、断面係数は、断面二次モーメントを断面の図心から上下縁までの距離で除した値です。断面二次モーメント、断面係数の詳細など下記も勉強しましょう。

断面二次モーメントとは？1分でわかる意味、計算式、h形鋼、公式、たわみとの関係

断面係数とは