- 【無料お試しキャンペーン中！】1級・2級建築士試験の構造の疑問を気軽に相談 初心者でもわかる！1級・2級建築士試験(構造)相談カフェ
- 管理人が業界分析！1日13円で建築業界がわかるLINE配信！ ⇒ まずはリンクをクリックして友だち追加！
モールの応力円とは？1分でわかる意味、導出、主応力の求め方は？
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
モールの応力円とは、縦軸にせん断応力、横軸に垂直応力をとり、断面に生じる垂直応力とせん断応力の関係を表す円です。モールの応力円を描くことで、簡単に断面の任意の角度に生じる垂直応力、せん断応力がわかります。なお、モールの応力円の方程式は、２軸方向に生じる応力のつりあいから求めます。今回はモールの応力円の意味、導出方法、主応力の求め方について説明します。二軸応力のつりあい、主応力の求め方は下記が参考になります。
2軸方向に生じる応力とは？任意断面の応力の求め方と力のつりあいは？
主応力の求め方は？2次元要素の主応力の導出方法、最大主応力、最小主応力の求め方は？
100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒ いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事
モールの応力円とは？
モールの応力円とは、縦軸にせん断応力、横軸に垂直応力をとり、断面に生じる垂直応力とせん断応力の関係を表す円です。下図にモールの応力円を示します。
上図のように、応力円を描ければ断面の任意の角度（2θ）における垂直応力、せん断応力が簡単にわかります（※なお、モールの応力円では、角度は2θが主値となる）。このように、モールの応力円を使えば
・視覚的に断面に生じる応力状態がわかる
という利点があります。一方で、現在は計算プログラムおよび、その結果を表示する視覚化プログラムが優れており、建築構造の実務でモールの応力円をあえて使う機会は、そう多くありません（応力円を使わなくても任意断面の応力が簡単にわかる。例えばFEMソフト等）。
さて、上図に示したモールの応力円を眺めると、モールの応力円には下記の特徴があることがわかります。
・応力円のｙ座標の中心はx軸（σ軸）と一致する、すなわち円の中心は（a,0）となる（aは任意の値）
・せん断応力τ＝0のとき、σは最大値（σ1）、最小値（σ3）をとる
・円の中心となる座標で、τは最大値（τmax）、最小値（τmin）をとる
・τmax、τminの値は、応力円の半径に相当する
・σ1とσ3の差は応力円の直径に相当する、すなわち、(σ1－σ3)/2はτの極値（最大値、最小値）となる
上記はモールの応力円に共通した特徴です。また、上記における垂直応力の最大値、最小値を併せて「主応力」といい、σ1を最大主応力、σ3を最小主応力、τmax、τminを主せん断応力といいます。
主せん断応力とは？1分でわかる意味、求め方、導出、方向、主応力との関係は？
さて、平面（2次元）の断面に応力が生じる場合の、モールの応力円の方程式を下記に示します。σ、τは断面の任意の角度における応力、σx、σyはx軸、ｙ軸に生じる垂直応力、τxyはせん断応力です。
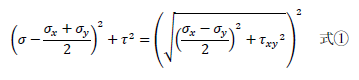
上式の導出方法は下記リンクあるいは後述を参考にしてください。
主応力の求め方は？2次元要素の主応力の導出方法、最大主応力、最小主応力の求め方は？
式①よりモールの応力円は
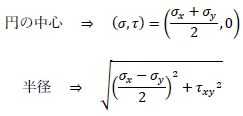
です。つまり、σx、σy、τxyの値が既知であれば、応力円を描けることがわかります。具体的にσx、σy、τxyが既知の場合における、モールの応力円の描き方の例を示しましょう。まず、下図のように縦軸にτ、横軸にσをとる直交座標を描きます。
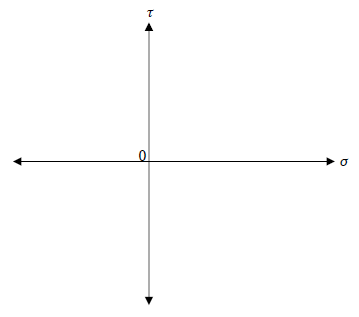
次に、σ軸上にσx、σyの点および垂直線を描きます。
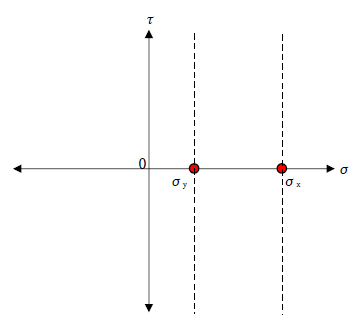
次に、(σ,τ)=(σx,τxy)、(σ,τ)=(σy,－τxy)となる点を定めて線を結び、この線が直径となる円を描けば、応力円の外形が描けます。
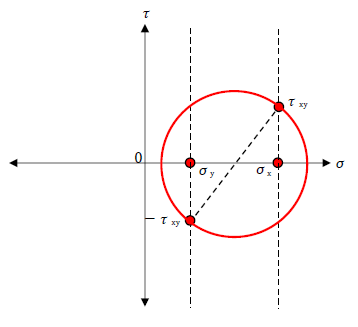
以上のように、σx、σy、τxyからモールの応力円が描け、あらゆる断面の垂直応力、せん断応力の関係が得られる点はとても便利です。
モールの応力円の導出は？
前述したモールの応力円の方程式（式①）の導出は、平面（２次元）に生じる応力のつりあいを理解すれば簡単です。２軸方向に応力が生じる物体における任意断面の垂直応力、せん断応力を下記に示します。
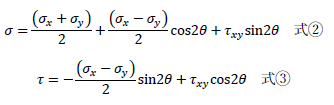
ここで円の方程式を思い出してください。円の方程式は
です。σとτの関係を円の方程式で表すことを目標に式を変形しましょう。式②の右辺を一部移項すると
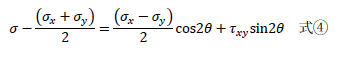
です。次に式④の両辺を二乗、式③の両辺を二乗して足し算します。すると
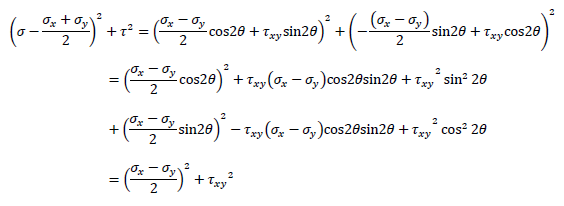
なので
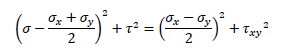
が得られます。さらに右辺を平方根の２乗の形に変形すると
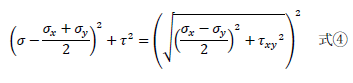
です。上記のように、σとτの関係が円の方程式として得られました。これがモールの応力円の方程式です。二軸方向の応力のつりあいの詳細は下記が参考になります。
2軸方向に生じる応力とは？任意断面の応力の求め方と力のつりあいは？
主応力の求め方は？
主応力の求め方を下記に示します。主応力の求め方は前述したモールの応力円の方程式から簡単に算定できます。モールの応力円よりτ＝0のとき主応力σ1、σ3を得ます。つまり、式④にτ＝0を代入すれば下式が算定できます。
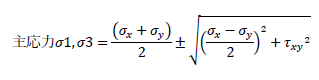
主応力の求め方の詳細は下記が参考になります。
主応力の求め方は？2次元要素の主応力の導出方法、最大主応力、最小主応力の求め方は？
まとめ
今回はモールの応力円について説明しました。モールの応力円とは、縦軸にせん断応力、横軸に垂直応力をとり、せん断応力と垂直応力の関係を表した円です。モールの応力円を使うことで、視覚的に垂直応力、せん断応力の関係が明らかになります。モールの応力円の方程式を理解する場合、下記も勉強しましょう。
2軸方向に生じる応力とは？任意断面の応力の求め方と力のつりあいは？
主応力の求め方は？2次元要素の主応力の導出方法、最大主応力、最小主応力の求め方は？
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
▼人気の記事ベスト３▼
- 1.断面係数の計算方法を本当にわかっていますか？→断面係数とは？
- 2.丸暗記で良いと思ったら大間違い→断面二次モーメントとは何か？
- 3.違いを適切に説明できますか？→等分布荷重とは？集中荷重との違いや使い方について
▼用語の意味知らなくて大丈夫？▼
▼同じカテゴリの記事一覧▼
- 2軸方向に生じる応力とは？任意断面の応力の求め方と力のつりあいは？
- 主応力の求め方は？2次元要素の主応力の導出方法、最大主応力、最小主応力の求め方は？
- 第一主応力とは？1分でわかる意味、求め方、最大主応力と最小主応力の違い、方向は？
- 最大主応力とは？1分でわかる意味、求め方、マイナスの値、圧縮・引張との関係、最小主応力の求め方は？
- 最大主応力と最小主応力の違いは？1分でわかる意味、求め方、最大主応力と最小主応力のマイナスと引張・圧縮の関係は？
- 主応力差とは？1分でわかる意味、せん断応力との関係、最大主応力の方向、求め方は？
- 主応力軸とは？1分でわかる意味、求め方、最大主応力、最小主応力の求め方は？
- 主せん断応力とは？1分でわかる意味、求め方、導出、方向、主応力との関係は？
- 主せん断応力の求め方は？1分でわかる意味、導出、モールの応力円との関係は？
▼カテゴリ一覧▼
- 建築物と構造力学の関係(まずは、苦手な勉強の進め方から)
- モデル化を学ぶ(まずは、構造物のモデル化から)
- 静定構造物の解き方を学ぶ(まずは、静定構造物に関する基礎用語から)
- 断面の性質を学ぶ(まずは、断面図形に関する基礎用語から)
- 梁のたわみを学ぶ(まずは、梁のたわみと基礎用語から)
- 座屈を学ぶ(まずは、座屈-基礎用語-から)
▼他の勉強がしたい方はこちら▼
【読まれています】管理人による建築業界の分析！
1日13円で建築業界がわかるLINE配信！。
わかる1級建築士の計算問題解説書
あなたは数学が苦手ですか？
【有料メルマガの初回資料が今だけ無料！】1日約13円で情報をアップデート！
有料メルマガを無料で見てみませんか？⇒ 忙しい社会人、学生のためのビルディング・アップデート
わかる2級建築士の計算問題解説書！
【30%OFF】一級建築士対策も◎！構造がわかるお得な用語集
更新情報
- 当サイトでは、ほぼ毎日、記事更新・追加を行っております。
- 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。
- 新着記事一覧
プロフィール
- 略歴▼
- 名前 ハナダユキヒロ/MITUME lab主宰.（筆者のコラムはこちら）
- 2010年 弊サイトを開設
- 2010～2017年 国立大学大学院修了
- 2017年12月に当HPが書籍化。
- 「わかる構造力学」
- 2022年4月に「わかる構造力学」の改訂版出版。
- 「わかる構造力学(改訂版)」
- 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。
- 自己紹介▼
- 建築学生が学ぶ「構造力学」とは？
- とりあえず10記事▼
- 初めましての方に10記事用意しました
- おすすめ書籍紹介▼
- ハナダユキヒロが建築関連書籍の良書を選びました
建築の本、紹介します。▼
同じカテゴリの記事一覧
- 2軸方向に生じる応力とは？任意断面の応力の求め方と力のつりあいは？
- 主応力の求め方は？2次元要素の主応力の導出方法、最大主応力、最小主応力の求め方は？
- 第一主応力とは？1分でわかる意味、求め方、最大主応力と最小主応力の違い、方向は？
- 最大主応力とは？1分でわかる意味、求め方、マイナスの値、圧縮・引張との関係、最小主応力の求め方は？
- 最大主応力と最小主応力の違いは？1分でわかる意味、求め方、最大主応力と最小主応力のマイナスと引張・圧縮の関係は？
- 主応力差とは？1分でわかる意味、せん断応力との関係、最大主応力の方向、求め方は？
- 主応力軸とは？1分でわかる意味、求め方、最大主応力、最小主応力の求め方は？
- 主せん断応力とは？1分でわかる意味、求め方、導出、方向、主応力との関係は？
- 主せん断応力の求め方は？1分でわかる意味、導出、モールの応力円との関係は？
- HOME > 構造力学の基礎 > モールの応力円とは？1分でわかる意味、導出、主応力の求め方は？
- 1級の過去問(計算)解説
- 限定メルマガ
- わかる建築構造の用語集・図解集
- 1頁10円！PDF版の学習記事