1. HOME > 水理学の基礎 > 流積とは？1分でわかる意味、円の求め方と公式、潤辺、径深との関係

流積とは？1分でわかる意味、円の求め方と公式、潤辺、径深との関係

流積（りゅうせき）とは、水路で水が流れる範囲の断面積です。用語の名前だけ聞くと難しそうですが、要するに「断面積」を求めればよいです。水路は開水路（かいすいろ）や閉水路（へいすいろ）など、断面形状の違いにより流積の計算式が変わることも覚えてください。今回は流積の意味、円の求め方と公式、潤辺、径深との関係について説明します。潤辺、径深の意味は下記が参考になります。

潤辺とは？1分でわかる意味、台形水路、円形の潤辺の求め方、径深との関係

径深とは？1分でわかる意味、求め方、公式、単位、水深との違い

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

流積とは？

流積（りゅうせき）とは、水路で水が流れる範囲の断面積です。下図をみてください。これが流積です。

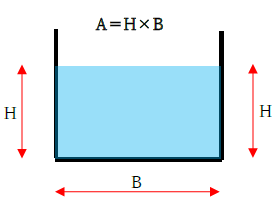
水路の形状で、水の流れる範囲は変わります。上図のように長方形水路なら、流積は長方形の断面積を計算すれば良いです。一方、下図のように台形水路の場合、台形の断面積＝流積です。

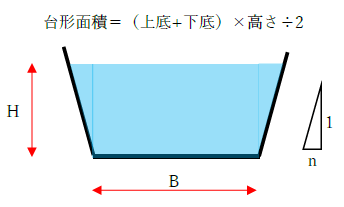
要するに流積は、水が流れる部分の水路の断面積です。なお前述したような「開いている形状」の水路を、開水路（かいすいろ）といいます。下図の円形（管状）の水路を、閉水路といいます。

円、長方形、台形の流積の求め方と公式

円、長方形、台形の流積の公式を下記に示します。

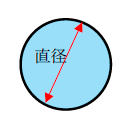
円形水路の流積　⇒　円周率×直径×直径÷4

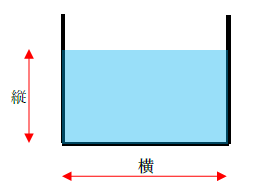
長方形水路の流積　⇒　縦×横

台形水路の流積　⇒　（上底+下底）×高さ÷2

前述した公式を使って、実際に台形水路の流積を求めましょう。

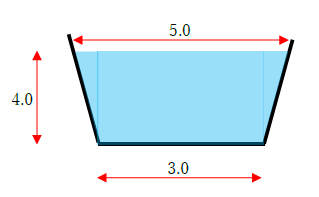
公式に当てはめれば良いので簡単ですね。まず上底＝5.0m、下底＝3.0m、高さ＝4.0mです。よって、

台形水路の流積＝（上底+下底）×高さ÷2＝（3.0+5.0）×4.0÷2＝16.0㎡

です。

流積と潤辺、径深の関係

流積をA、潤辺をS、径深をRとするとき、３つの値は下記の関係にあります。

R=A÷S

Rは径深（けいしん）といい、平均的な水深を意味します。径深、潤辺の詳細は下記が参考になります。

径深とは？1分でわかる意味、求め方、公式、単位、水深との違い

潤辺とは？1分でわかる意味、台形水路、円形の潤辺の求め方、径深との関係

まとめ

今回は流積について説明しました。意味が理解頂けたと思います。流積は、水路で水が流れる範囲の断面積です。よって、水路形状に応じて流積の公式（求め方）は変わります。難しく考える必要はありません。円、長方形、台形など基本的な図形の面積の計算式を再確認しましょう。下記も参考になります。

径深とは？1分でわかる意味、求め方、公式、単位、水深との違い

潤辺とは？1分でわかる意味、台形水路、円形の潤辺の求め方、径深との関係

断面積とは？1分でわかる求め方、長方形と円の公式、単位、計算方法、直径との関係

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

▼人気の記事ベスト３▼

• 1.断面係数の計算方法を本当にわかっていますか？→断面係数とは？
• 2.丸暗記で良いと思ったら大間違い→断面二次モーメントとは何か？
• 3.違いを適切に説明できますか？→等分布荷重とは？集中荷重との違いや使い方について

▼用語の意味知らなくて大丈夫？▼

▼同じカテゴリの記事一覧▼

• アルキメデスの原理とは？1分でわかる意味、証明、浮力との関係、公式
• 浮力とは？1分でわかる意味、原理、公式、体積、単位、重力との関係
• 浮力の単位は？1分でわかる意味、単位、g、kgf、n、公式との関係
• 径深とは？1分でわかる意味、求め方、公式、単位、水深との違い
• 潤辺とは？1分でわかる意味、台形水路、円形の潤辺の求め方、径深との関係
• 潤辺の読み方は？1分でわかる読み方、意味、求め方、径深との関係
• 流速とは？1分でわかる意味、単位、平均流速との関係、マニングの公式
• マニングの公式とは？1分でわかる意味、径深、粗度係数、勾配、平均流速の公式との関係
• 粗度係数とは？1分でわかる意味、単位、求め方、粗度係数の値と鋼、コンクリート

▼カテゴリ一覧▼

▼他の勉強がしたい方はこちら▼

• 構造力学の基礎
• 構造計算の基礎
• 鋼構造（鉄骨構造）の基礎
• 鉄筋コンクリート造の基礎
• 基礎構造
• 数学の基礎
• 水理学の基礎
• 材料力学の基礎
• 構造力学の応用
• 耐震設計の基礎
• 有限要素法の基礎
• 一級・二級建築士の勉強
• 建築学生向け就職、学業情報
• 建築構造に関する一般向け情報
• 計算プログラムから構造力学を学ぶ

【有料メルマガの初回資料が今だけ無料！】1日約13円で情報をアップデート！

有料メルマガを無料で見てみませんか？⇒　忙しい社会人、学生のためのビルディング・アップデート

更新情報

• 当サイトでは、ほぼ毎日、記事更新・追加を行っております。


• 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。


• 新着記事一覧

プロフィール

• 略歴▼
• 名前　ハナダユキヒロ/MITUME lab主宰.（筆者のコラムはこちら）
• 2010年　弊サイトを開設
• 2010～2017年　国立大学大学院修了
• 2017年12月に当HPが書籍化。
• 「わかる構造力学」
• 2022年4月に「わかる構造力学」の改訂版出版。
• 「わかる構造力学(改訂版)」


• 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。


• 自己紹介▼
• 建築学生が学ぶ「構造力学」とは？


• とりあえず10記事▼
• 初めましての方に10記事用意しました


• おすすめ書籍紹介▼
• ハナダユキヒロが建築関連書籍の良書を選びました

建築の本、紹介します。▼

人気の記事ベスト３

• 一級建築士が転職すべき1つの理由と、転職後の年収を調べる方法
• 断面係数とは
• 等分布荷重とは？集中荷重との違いや使い方について

同じカテゴリの記事一覧

• アルキメデスの原理とは？1分でわかる意味、証明、浮力との関係、公式
• 浮力とは？1分でわかる意味、原理、公式、体積、単位、重力との関係
• 浮力の単位は？1分でわかる意味、単位、g、kgf、n、公式との関係
• 径深とは？1分でわかる意味、求め方、公式、単位、水深との違い
• 潤辺とは？1分でわかる意味、台形水路、円形の潤辺の求め方、径深との関係
• 潤辺の読み方は？1分でわかる読み方、意味、求め方、径深との関係
• 流速とは？1分でわかる意味、単位、平均流速との関係、マニングの公式
• マニングの公式とは？1分でわかる意味、径深、粗度係数、勾配、平均流速の公式との関係
• 粗度係数とは？1分でわかる意味、単位、求め方、粗度係数の値と鋼、コンクリート