HOME > 数学の基礎 > ベクトルの足し算とは？1分でわかる意味、計算、絶対値の求め方、図示の方法

【無料お試しキャンペーン中！】1級・2級建築士試験の構造の疑問を気軽に相談　初心者でもわかる！1級・2級建築士試験(構造)相談カフェ
管理人が業界分析！1日13円で建築業界がわかるLINE配信！　⇒　まずはリンクをクリックして友だち追加！

ベクトルの足し算とは？1分でわかる意味、計算、絶対値の求め方、図示の方法

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

ベクトルの足し算は「方向（向き）」を考慮して足し算します。ベクトルとは大きさと方向をもつ量です。よって「1+1＝2」のような大きさだけの足し算とは違います。不思議かもしれませんが方向が異なるベクトルの足し算は「1+1＝1.4」という結果になることもあります。

ベクトルを表す方法として(2,3)のように成分で表すか、有向線分を用いて図示する方法があります。または、その両方を用いてベクトルを表すことも可能です。今回はベクトルの足し算と意味、計算、絶対値の求め方、図示の方法について説明します。有効線分、ベクトルの成分の関係は下記が参考になります。

有向線分とは？1分でわかる意味（定義）、書き方、読み方、ベクトルとの違い

ベクトルの成分表示とは？3分でわかる意味、成分の表し方、大きさとの関係

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

ベクトルの足し算とは？計算

ベクトルの足し算は「方向（向き）」を考慮して足し算します。例えば「1」という大きさで異なる方向を持つベクトルを足し算すると「1+1＝1.41」という結果になることもあります。

一方「お金」など、普段の生活では「大きさだけをもつ量」を使うことが多いです。大きさだけを持つ量は「1+1＝2」のように、単純に足し算すればよいですね。

ベクトルの足し算で躓く方は「ベクトルの足し算と大きさだけの足し算」を混同していることが多いです。

まずは「ベクトルの足し算と、大きさだけの足し算は全く違う」ことを覚えてください。

下図をみてください。ベクトルは有向線分で図示することが可能です。線分の長さがベクトルの大きさ、線分の向きがベクトルの向きを表します。有向線分の詳細は下記が参考になります。

有向線分とは？1分でわかる意味（定義）、書き方、読み方、ベクトルとの違い

図　ベクトルと有向線分

異なる方向を持つ２つのベクトルを足し算した結果を下図に示しました。

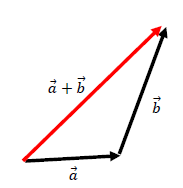
図　ベクトルの足し算

数式で表すと２つのベクトルの足し算は

$\vec{a}+\vec{b}$

です。上記の結果をみて「なんだ、文字や数の足し算と同じだ」と思っているなら誤りです。何度も言うように「ベクトルの足し算は、大きさの足し算と違う」のです。

有向線分の長さが「ベクトルの大きさ」でした。明らかに、２つのベクトルを足し算した線分の長さは、a、bの長さをそれぞれ足し算した結果より「短い」ですよね。

これはベクトルaの大きさ、bの大きさを足し算した結果とベクトル(a+b)の大きさは全く異なることを意味します。

なお、ベクトルの大きさは

と表します。よって

a+b

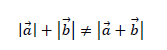
といえます。

さて、ベクトルの足し算は「成分表示」すると理解しやすいと思います。ベクトルは大きさと方向を持つ量です。よって、座標に成分を示せば「線分の方向、長さ」を図示できます。ベクトルを成分表示する方法は下記をご覧ください。

ベクトルの成分表示とは？3分でわかる意味、成分の表し方、大きさとの関係

下図に２つのベクトルと、足し算したベクトルを示しました。

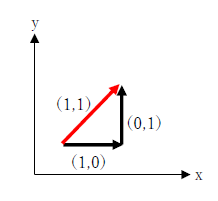
図　ベクトルの足し算と成分表示

ベクトルaの成分は（1,0）、bのベクトルは（0,1）です。※()内の成分は点の位置ではなく、距離を表しています。

よってa、b(ベクトル)を足し算したベクトルcは

a+b

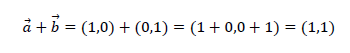
です。ベクトルｃの成分は（1,1）だと分かりました。また足し算したベクトルの大きさは、ピタゴラスの定理より算定できます。上図の例だと、ベクトルの大きさ（線分の長さ）は1.41になります。ベクトルの大きさの詳細は下記をご覧ください。

ベクトルの大きさとは？1分でわかる意味と求め方、記号、二乗、絶対値との関係

またベクトルの足し算でも交換法則と結合法則が成立します。下記に示します。

ベクトルの交換法則

交換法則、結合法則の詳細は下記をご覧下さい。

交換法則とは？1分でわかる意味、読み方、計算、減法と除法、分配法則との関係

結合法則とは？1分でわかる意味、読み方、式と計算、分配法則、除法との関係

ベクトルの足し算を図示する方法

ベクトルは有向線分で図示します。当然、ベクトルの足し算も図示できます。ただ、慣れるまでベクトルの足し算の図示の仕方が難しいかもしれません。

下図の２つのベクトルの足し算を図示してください。

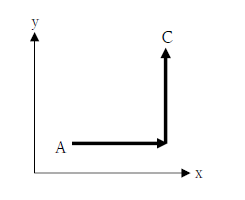
図　ベクトルの足し算を図示する方法

これを考える時、マラソンの「スタート」と「ゴール」をイメージすると良いです。矢印の無い点の「A点」がスタートです。ではどこがゴールかというと、矢印の先端であるC点です。

よってベクトルの足し算はスタートA点からゴールのC点まで直線で結んだ線分です。

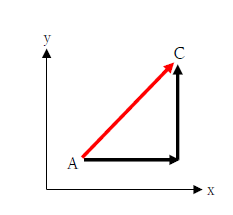
図　ベクトルの足し算と図示

間違ってもC点からA点に向かって矢印を引かないでくださいね。それではゴールとスタートが逆さになってしまいます。

ベクトルの絶対値の求め方

ベクトルの絶対値をの求め方を下記に示します。

ベクトル絶対値

a1、a2、b1、b2は２点の座標です。上記は２点間の距離をピタゴラスの定理で求めています。ベクトルの絶対値（大きさ）は線分の長さと同じなので、距離を算定すれば絶対値が求められます。

ベクトルの大きさは下記も参考になります。

ベクトルの大きさとは？1分でわかる意味と求め方、記号、二乗、絶対値との関係

まとめ

今回はベクトルの足し算について説明しました。意味が理解頂けたと思います。ベクトルの足し算は大きさだけの足し算とは違います。方向を考慮するため「1+1≠2」のような結果になるのです。お金の足し算のように「大きさだけを持つ量の足し算」をいったん忘れて、ベクトルの足し算を勉強しましょう。下記も参考になります。

ベクトルの大きさとは？1分でわかる意味と求め方、記号、二乗、絶対値との関係

ベクトルの成分表示とは？3分でわかる意味、成分の表し方、大きさとの関係