弾性座屈荷重とは?計算、断面二次モーメントとの関係、単位、弾性座屈荷重は柱の曲げ剛性に反比例する?
【管理人おすすめ!】セットで3割もお得!大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集&図解集セット(※既に26人にお申込みいただきました!)
弾性座屈荷重とは、材料の線形弾性を前提とした座屈荷重で「オイラー座屈荷重」ともいいます。弾性座屈荷重Pcrの計算式はPcr=π^2×EI/Lk^2です。Eはヤング係数、Iは断面二次モーメント、Lkは座屈長さ(有効座屈長さ)です。今回は、弾性座屈荷重の意味、計算、断面二次モーメントとの関係、単位、弾性座屈荷重は柱の曲げ剛性に反比例するか説明します。座屈荷重、座屈の詳細は下記が参考になります。
100円から読める!ネット不要!印刷しても読みやすいPDF記事はこちら⇒ いつでもどこでも読める!広告無し!建築学生が学ぶ構造力学のPDF版の学習記事
弾性座屈荷重とは?計算、断面二次モーメントとの関係は?
弾性座屈荷重とは、材料の線形弾性を前提とした座屈荷重で「オイラー座屈荷重」ともいいます。弾性座屈荷重Pcrはの計算は下式の通りです。Eはヤング係数、Iは断面二次モーメント、Lkは座屈長さ(有効座屈長さ)です。
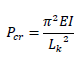
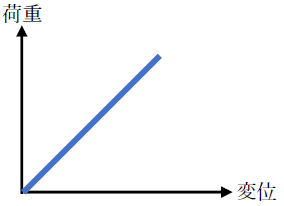
材料の線形弾性とは下図に示すように、荷重と変位の関係が線形で、かつ、弾性の性質(力を加えると変形し、力を取り除くと変形が無くなる性質)をもつことです。
ある棒が完全に線形弾性で、かつ、初期不整(残留ひずみ、応力、ずれ等)が無ければ、座屈荷重は弾性座屈荷重の式で算定できます。しかし鋼のように、降伏したのち材料の弾性が失われる場合、弾性座屈荷重の計算式は使用できず、非弾性荷重の考え方を必要とします。さて、弾性座屈荷重の式を断面積Aで割り算すると、単位断面積あたりの弾性座屈荷重すなわち「座屈応力度σcr」が得られます。
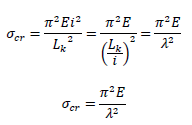
上式のように、座屈応力度は細長比λが小さいほど大きくなるのですが、上式に従えば、λを0に近づけると座屈応力度は無限大に大きくなり、材料のもつ降伏応力度や圧縮強度そのものを計算上終超えてしまいます。
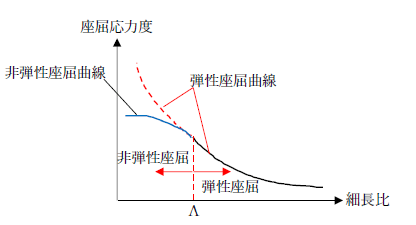
当然そのようなことにはならず、細長比をある値より小さくしても、前述した弾性座屈応力の理論式より小さい値になることが分かっています。これは部材の初期不整(残留ひずみ、応力、ずれ等)の影響により、部分的に部材が塑性化を起こし、弾性座屈が成立しなくなっているためです。この弾性座屈と非弾性座屈の境界の細長比を「限界細長比」といいます。限界細長比の詳細は下記が参考になります。
弾性座屈荷重の計算と断面二次モーメント
弾性座屈荷重の計算式をみると明らかなように、弾性座屈荷重は、断面二次モーメントが大きいほど大きい値です。つまり、断面二次モーメントが大きい部材(固い部材)ほど座屈しにくいことを意味します。
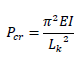
断面二次モーメントとは?1分でわかる意味、計算式、h形鋼、公式、たわみとの関係
弾性座屈荷重の単位は?
弾性座屈荷重の単位はN、kNです。座屈荷重の計算式より、ヤング係数の単位はN/mm2、断面二次モーメントの単位はmm4、Lk^2の単位はmm2なので、整理すると弾性座屈荷重の単位はNだとわかりますね。
弾性座屈荷重は柱の曲げ剛性に反比例する?
弾性座屈荷重は柱の曲げ剛性に比例します。反比例しません。曲げ剛性とは曲げモーメントに対する部材のかたさで「EI」のことです。弾性座屈荷重は下式で求めるので、EIが大きくなるほどPcrは大きくなる、すなわち、弾性座屈荷重は曲げ剛性に比例します。
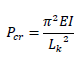
まとめ
今回は弾性座屈荷重について説明しました。弾性座屈荷重とは、材料の線形弾性を前提とした座屈荷重で「オイラー座屈荷重」ともいいます。弾性座屈荷重Pcrの計算式はPcr=π^2×EI/Lk^2です。座屈、座屈荷重の詳細など下記も勉強しましょう。
【管理人おすすめ!】セットで3割もお得!大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集&図解集セット(※既に26人にお申込みいただきました!)
▼スポンサーリンク▼
▼用語の意味知らなくて大丈夫?▼

▼同じカテゴリの記事一覧▼
- 座屈とは?座屈荷重の基礎知識と、座屈の種類
- 座屈荷重とは?計算式、単位、断面二次モーメントとの関係は?
- 局部座屈とは?対策、幅厚比の計算、板座屈、全体座屈との違いは?
- オイラー座屈とは?座屈荷重の計算式と導出方法
- 板座屈とは?1分でわかる意味、読み方、英語、幅厚比、局部座屈の関係
- 細長比と座屈長さ、断面二次半径の関係
- 細長比の読み方は?1分でわかる意味、小さい、大きいの考え方、計算方法は?
- 細長比の単位は?1分でわかる意味、読み方、求め方、小さいとどうなる?
- 細長比が大きいとどうなる?1分でわかる計算と意味、小さいとどうなる?
- 限界細長比とは?記号、記号の読み方、許容圧縮応力度との関係
▼カテゴリ一覧▼
- 建築物と構造力学の関係(まずは、苦手な勉強の進め方から)
- モデル化を学ぶ(まずは、構造物のモデル化から)
- 静定構造物の解き方を学ぶ(まずは、静定構造物に関する基礎用語から)
- 断面の性質を学ぶ(まずは、断面図形に関する基礎用語から)
- 梁のたわみを学ぶ(まずは、梁のたわみと基礎用語から)
▼他の勉強がしたい方はこちら▼
更新情報
- 当サイトでは、ほぼ毎日、記事更新・追加を行っております。
- 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。
- 新着記事一覧
プロフィール

- 略歴▼
- 名前 ハナダユキヒロ/MITUME lab代表.
- 2010年 弊サイトを開設
- 2010~2017年 国立大学大学院修了
- 2017年12月に当HPが書籍化。
- 「わかる構造力学」
- 2022年4月に「わかる構造力学」の改訂版出版。
- 「わかる構造力学(改訂版)」
- 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。
- 当サイトの目的▼
- 建築学生が学ぶ「構造力学」の目的
- とりあえず10記事▼
- 初めましての方に10記事用意しました
- おすすめ書籍紹介▼
- ハナダユキヒロが建築関連書籍の良書を選びました
同じカテゴリの記事一覧
- HOME > 構造力学の基礎 > 弾性座屈荷重とは?計算、断面二次モーメントとの関係、単位、弾性座屈荷重は柱の曲げ剛性に反比例する?
- 1級の過去問(計算)解説
- 限定メルマガ
- わかる建築構造の用語集・図解集
- 1頁10円!PDF版の学習記事




