1. HOME > 構造力学の基礎 > 横弾性係数とは？意味、求め方、導出方法【図解】

横弾性係数とは？意味、求め方、導出方法【図解】

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

横弾性係数はせん断力に対するかたさ（変形のしにくさ）を表す材料固有の値です。

横弾性係数が大きいほど、せん断力に対して「かたい（変形しにくい）」といえます。横弾性係数Gを求める式は

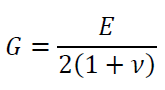
で、Eは縦弾性係数（ヤング係数）、νは材料のポアソン比です。横弾性係数が大きいほど、せん断力τに対してΔLが小さくなります。

なお、縦弾性係数は圧縮力、引張力に対するかたさを表す材料固有の値です。

今回は、横弾性係数の意味、縦弾性係数との違い、単位、ステンレス、鋼の値、求め方、ポアソン比との関係、導出方法について説明します。

せん断弾性係数、ヤング係数の詳細は下記が参考になります。

せん断弾性係数とは？ヤング率との関係、一覧とコンクリートのせん断弾性係数の計算、単位、導出方法は？

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

横弾性係数とは？縦弾性係数との違いは？

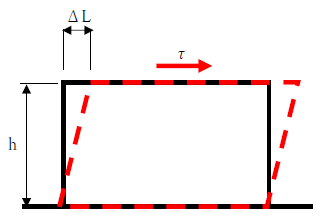
横弾性係数はせん断力に対するかたさ（変形のしにくさ）を表す材料固有の値です。下図をみてください。

せん断力τが作用するとき、横弾性係数が大きいほど変形量ΔLは小さくなり、横弾性係数が小さいと変形量ΔLは大きくなります。

つまり

・横弾性係数が大きい　⇒　せん断力に対して、かたい材料

・横弾性係数が小さい　⇒　せん断力に対して、柔らかい材料

です。横弾性係数は材料固有の値なので、鉄筋コンクリート、鋼、木、ステンレス等に応じて値が変わります。

一方、材質が同じであれば部材の断面形状が異なっても横弾性係数は同じ値です。

なお、横弾性係数は「せん断弾性係数」ともいいます。

横弾性係数と似た用語に「縦弾性係数」があります。横弾性係数と縦弾性係数の違いは下記の通りです。

・横弾性係数　⇒　せん断力に対するかたさ（変形のしにくさ）を表す材料固有の値

・縦弾性係数　⇒　圧縮力、引張力に対する（変形のしにくさ）を表す材料固有の値

なお曲げモーメントは、引張と圧縮の組み合わせによる応力なので、縦弾性係数が対応する抵抗値です。

また、横弾性係数の記号は「G」、縦弾性係数は一般的に「E」とします。なお、縦弾性係数は単に「弾性係数」または「ヤング係数、ヤング率」ともいいます。

ヤング係数の詳細は下記が参考になります。

ヤング係数とは？求め方と公式、単位、材料ごとの値【図解】

さて、横弾性係数を求める式は

・G=E×1／2（1+ν）

です。Ｇは横弾性係数、Ｅは縦弾性係数、νはポアソン比です。上式より、横弾性係数は縦弾性係数に比例する、

すなわち、縦弾性係数が大きいほど横弾性係数も大きいことがわかります。また、GはEと比例関係にありますが、

前述したGの式より概ねEの値の半分以下になります。

下図をみてください。せん断力を受ける箱状の部材があります。このとき、せん断力τが変形量はΔLです。

まず、せん断力τと、横弾性係数G、せん断歪γによる関係式（フックの法則）を示すと下記になります。

・τ＝Gγ

上式は普通のフックの法則と同じ考えですが、せん断歪γは伸び縮みの量ではなく、角度で表します。

上図の例でいうと、

γ＝ΔL／ｈ

です。

横弾性係数の単位は？

横弾性係数の単位は「N/mm2」または「GPa」を用います。つまり、縦弾性係数と同じ単位です。ヤング係数の単位の詳細は下記をご覧ください。

ヤング率の単位は？1分でわかる単位、意味、読み方、MPa、kgf/mm2との関係

横弾性係数とポアソン比の関係は？

前述したように、横弾性係数はポアソン比と関係します。下式をみてください。

G＝E／2（1+ν）

ポアソン比が大きいほど、横弾性係数は小さくなります。ポアソン比が大きいと、主軸直交方向の変形が大きいからです。

ステンレス、鋼、コンクリートの横弾性係数と求め方は？

コンクリートと鋼の横弾性係数は下記となります。

・ステンレスの横弾性係数　⇒　G=E／2.60≒74300N/mm2

・鋼の横弾性係数　⇒　G=E／2.60≒79000N/mm2

・コンクリートの横弾性係数　⇒　G= E／2.33

横弾性係数の求め方を示しましょう。鋼の弾性係数は2.05×105N/mm2、ポアソン比は0.3とすれば鋼の弾性係数は

G=(2.05×10^5)/2（1+0.3） =(2.05×10^5)/2.6=78846≒79000N\/mm^2

です。各材料の横弾性係数の一覧は下記をご覧ください。

横弾性係数の一覧は？3分でわかる値、単位、縦弾性係数との違い

横弾性係数とポアソン比の関係は？

横弾性係数とポアソン比の関係を下記に示します。下式の通り、ポアソン比νは分母にあるので、

ポアソン比が大きいほど横弾性係数は小さくなり、ポアソン比が大きいほど横弾性係数は大きくなります。

・G=E×1／2（1+ν）

ポアソン比の基礎知識、縦弾性係数との関係

横弾性係数の導出方法は？

下図をみてください。せん断力τ、変形ΔLが生じています。

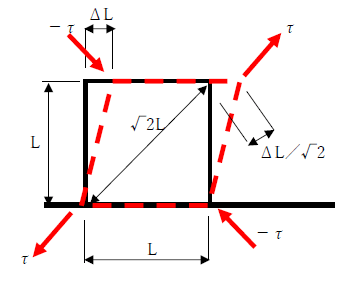
まずせん断力と横弾性係数には下記の関係があります。

τ＝Gγ

γ＝ΔL／ｈ

また上図のように変形する物体は、見方を変えると（主軸を変える。下図参照）引張と圧縮力が作用しています。

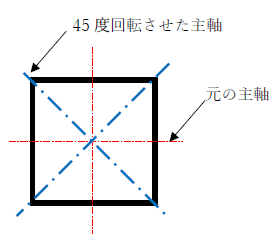
このように応力は、主軸を変えることで値が変化するベクトルの要素を持っています。

上図のようにせん断力τが作用する部材も、主軸を45度回転させれば垂直応力度が作用すると考えてよいです。

では、どうやって主軸を回転させた応力が計算できるのか。これは「主応力」を計算する式を用います。下式は主応力の算定式です。

σθ＝(σx+σy)2+(σx－σy)2×cos2θ+τsin2θ

θは任意の角度、σθは任意の角度を主軸として作用する垂直応力度、σxはX方向の応力度、σyはY方向の応力度、τはせん断応力度です。

今回、せん断応力度しか作用していないので

σx＝0

σy＝0

τ＝τ

です。さらに、θ＝45度＝π/4なので、これらを代入すると、

σθ＝τsin2θ＝τsinπ/2＝τ

です。さて、主軸を変えた場合の垂直応力度τが作用するとき、歪εは下式です。

ε＝(ΔL／√2)／√2L

　＝ΔL／2L

　＝γ／2

また、σ＝Eεの関係から歪εを計算します。

ε＝σ／E

＝（σ／E－σν／E）

＝（τ／E+τν／E）

　＝τ／E×（1+ν）

なぜ、ε＝（σ／E－σν／E）とするのか。σ／Eは主軸方向の歪ですが、主軸直交方向の歪も主軸方向の歪に関係するからです。

両方向から応力が作用するとき、縦と横、両方向の歪を考慮するからです。詳しくはポアソン比の記事で書いています。

ポアソン比の基礎知識、縦弾性係数との関係

以上より、下記の２式を関係づけます。

ε＝τ／E×（1+ν）

ε＝γ／2＝τ／2G

τ／2G＝τ／E×（1+ν）

G＝E／2（1+ν）

まとめ

今回は横弾性係数について説明しました。横弾性係数とは、せん断力に対するかたさ（変形のしにくさ）を表す材料固有の値です。

横弾性係数が大きいほど、せん断力に対してかたい、横弾性係数が小さいほど、せん断力に対して柔らかいと言えます。

なお、縦弾性係数は圧縮力、引張力に対するかたさを表す材料固有の値です。縦弾性係数はヤング係数、横弾性係数はせん断弾性係数と言います。

ヤング係数とは？求め方と公式、単位、材料ごとの値【図解】

せん断弾性係数とは？ヤング率との関係、一覧とコンクリートのせん断弾性係数の計算、単位、導出方法は？

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

▼スポンサーリンク▼

▼初回無料！月額約400円で業界最新情報をゲット！▼

「建築業界の最新動向」を最速でキャッチ。

今すぐ無料で試してみよう！⇒　ビルディング・アップデート

更新情報

• 当サイトでは、ほぼ毎日、記事更新・追加を行っております。


• 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。


• 新着記事一覧

プロフィール

• 
• 略歴▼
• 名前　ハナダユキヒロ/MITUME lab代表.
• 2010年　弊サイトを開設
• 2010～2017年　国立大学大学院修了
• 2017年12月に当HPが書籍化。
• 「わかる構造力学」
• 2022年4月に「わかる構造力学」の改訂版出版。
• 「わかる構造力学(改訂版)」


• 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。


• 当サイトの目的▼
• 建築学生が学ぶ「構造力学」の目的


• とりあえず10記事▼
• 初めましての方に10記事用意しました


• おすすめ書籍紹介▼
• ハナダユキヒロが建築関連書籍の良書を選びました

建築の本、紹介します。▼

▼建築・構造の疑問、専門家が回答！▼

「LINEで今すぐ質問 → 最短30分で返信」

友だち追加して無料相談→今すぐ質問する！

同じカテゴリの記事一覧

• フックの法則とは？1分でわかる意味、公式、単位、応力、ヤング率の関係
• 横弾性係数の一覧は？3分でわかる値、単位、縦弾性係数との違い
• せん断弾性係数とは？ヤング率との関係、一覧とコンクリートのせん断弾性係数の計算、単位、導出方法は？
• 弾塑性とは？1分でわかる意味、読み方、材料、弾性と塑性の違い
• 塑性域とは？1分でわかる意味、読み方、弾性域との違い、ヤング率と応力の関係
• 弾性域とは？1分でわかる意味、ひずみ、弾性変形と塑性変形、塑性域との違い
• ヤング係数ってなに？1分でわかるたった1つのポイント
• ヤング率が大きいとは？1分でわかる意味、かたさとの関係、ヤング率の大きい（高い）材料
• ヤング率の公式は？1分でわかる求め方、単位、公式と伸びの関係
• ヤング係数の求め方は？1分でわかる求め方、コンクリート、鋼材の値、グラフの傾きとの関係