単位円とは？1分でわかる意味、覚え方、表、sin、tanとの関係
単位円（たんいえん）とは、原点を中心とする半径１の円です。単位円の中に斜辺が１となる直角三角形をつくると、底辺と高さが1以下の値になります。扱いやすい数になるので、三角比の計算などに便利です。今回は単位円の意味、覚え方、表、sin、tanとの関係について説明します。三角比の詳細は下記が参考になります。
鋭角の三角比とは？1分でわかる意味、辺の長さと角度の関係、三平方の定理
三角比の定義は？１分でわかる定義、覚え方、表、直角三角形と単位円との関係
100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒ いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事
記事を書いた人
難解な構造力学、建築構造の用語を分かりやすく解説する専門家。高等専門学校在学中から建築学生が学ぶ「構造力学」を運営。その後、国立大学大学院⇒組織設計事務所⇒弊サイト運営に従事している。
著書：「わかる構造力学/工学社」、「わかる構造力学 改訂版/工学社」
LINEで質問したい方はこちら ⇒ 【好評】管理人にLINEで質問してみよう
単位円とは？sin、tanとの関係
単位円（たんいえん）とは、原点を中心とする半径１の円です。下図に単位円を示します。
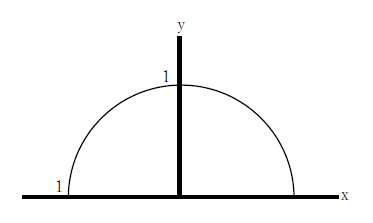
単位円の円周上に点Pを取ります。点Pの座標は（x,y）です。単位円の中心（原点）からPまで線を引きます。さらに点Pからｘ軸に向かって垂直線を下ろします。下図をみてください。単位円の中に直角三角形ができました。
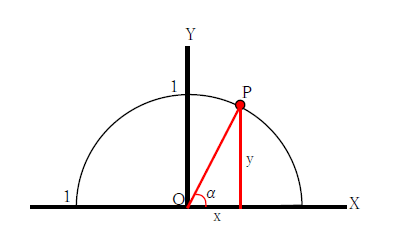
半径r=1なので直角三角形の三角比sin、cos、tanは下記となります。
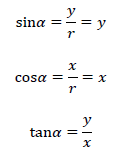
上記のように単位円の中に直角三角形を表すことで、三角比の値が「底辺」「高さ」の長さと一致します。簡単に三角比が求まるので便利ですね。三角比の求め方、意味などは下記も参考になります。
鋭角の三角比とは？1分でわかる意味、辺の長さと角度の関係、三平方の定理
三角比の定義は？１分でわかる定義、覚え方、表、直角三角形と単位円との関係
単位円の覚え方
単位円の覚え方は簡単です。まず平面座標を描きます。次に、原点Oを中心とする半径１の円を描けば完成です。「単位円＝半径１の円」と覚えておけばよいでしょう。
単位円と表の関係
よく使う三角比を表、単位円に表しました。下図と下表をみてください。
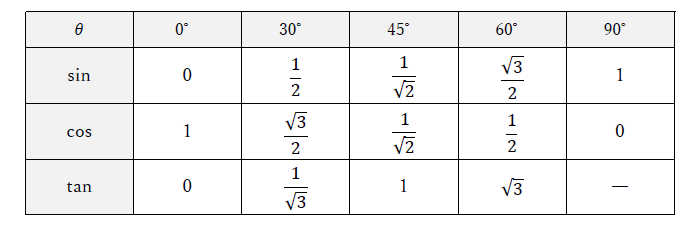
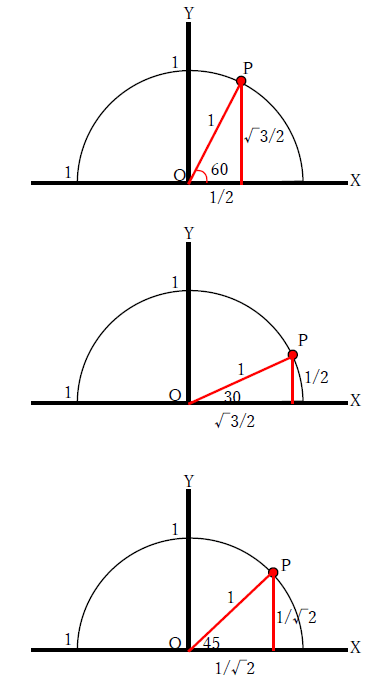
また鋭角が45°のとき、斜辺：底辺：高さ＝1：√2：√2の関係になります。これが直角二等辺三角形です。詳細は下記をご覧ください。
直角二等辺三角形の辺の長さは？1分でわかる求め方、公式、辺の長さと角度の関係、証明
まとめ
今回は単位円について説明しました。意味が理解頂けたと思います。単位円とは、原点を中心とする半径１の円です。単位円の中に直角三角形を表すと斜辺が１の三角形になります。鋭角が45°、30°、60°など、よく使う三角比を単位円に描いてみましょう。三角比の意味など下記も勉強しましょうね。
三角比の定義は？１分でわかる定義、覚え方、表、直角三角形と単位円との関係
鋭角の三角比とは？1分でわかる意味、辺の長さと角度の関係、三平方の定理
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
▼スポンサーリンク▼
▼【好評！】管理人おすすめ▼
- あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！
▼用語の意味知らなくて大丈夫？▼
▼同じカテゴリの記事一覧▼
- 三角比の定義は？１分でわかる定義、覚え方、表、直角三角形と単位円との関係
- 鋭角の三角比とは？1分でわかる意味、辺の長さと角度の関係、三平方の定理
- ピタゴラスの定理とは？1分でわかる意味、証明、3:4:5の関係、三平方の定理との違い
- sin90度の値は？1分でわかる値、1になる理由と求め方、cos90度が0になる理由
- cos30度の値は？1分でわかる分数、小数の値、求め方、cos45度、sin60度の値
- sin45度の値は？1分でわかる分数の値、求め方、cos45との違い、2分のルート2の関係
- sin60度の値は？1分でわかる意味、分数の値、cos30、cos45の値
- sin30度の値は？1分でわかる値、2分の1となる理由、三角比と分数、sin45度の関係
- tan45度の値は？1分でわかる意味、値、cos45度、sin45度との関係
▼カテゴリ一覧▼
▼他の勉強がしたい方はこちら▼
【好評】LINEで質問！
管理人に質問してみる？。
わかる1級建築士の計算問題解説書
【有料メルマガの初回資料が今だけ無料！】1日約13円で情報をアップデート！
有料メルマガを無料で見てみませんか？⇒ 忙しい社会人、学生のためのビルディング・アップデート
わかる2級建築士の計算問題解説書！
【30%OFF】一級建築士対策も◎！構造がわかるお得な用語集
更新情報
- 当サイトでは、ほぼ毎日、記事更新・追加を行っております。
- 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。
- 新着記事一覧
プロフィール
- 略歴▼
- 名前 ハナダユキヒロ/MITUME lab代表.
- 2010年 弊サイトを開設
- 2010～2017年 国立大学大学院修了
- 2017年12月に当HPが書籍化。
- 「わかる構造力学」
- 2022年4月に「わかる構造力学」の改訂版出版。
- 「わかる構造力学(改訂版)」
- 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。
- 自己紹介▼
- 建築学生が学ぶ「構造力学」とは？
- とりあえず10記事▼
- 初めましての方に10記事用意しました
- おすすめ書籍紹介▼
- ハナダユキヒロが建築関連書籍の良書を選びました
建築の本、紹介します。▼
▼【好評！】管理人おすすめ▼
- あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！
同じカテゴリの記事一覧
- 三角比の定義は？１分でわかる定義、覚え方、表、直角三角形と単位円との関係
- 鋭角の三角比とは？1分でわかる意味、辺の長さと角度の関係、三平方の定理
- ピタゴラスの定理とは？1分でわかる意味、証明、3:4:5の関係、三平方の定理との違い
- sin90度の値は？1分でわかる値、1になる理由と求め方、cos90度が0になる理由
- cos30度の値は？1分でわかる分数、小数の値、求め方、cos45度、sin60度の値
- sin45度の値は？1分でわかる分数の値、求め方、cos45との違い、2分のルート2の関係
- sin60度の値は？1分でわかる意味、分数の値、cos30、cos45の値
- sin30度の値は？1分でわかる値、2分の1となる理由、三角比と分数、sin45度の関係
- tan45度の値は？1分でわかる意味、値、cos45度、sin45度との関係
- HOME > 数学の基礎 > 単位円とは？1分でわかる意味、覚え方、表、sin、tanとの関係
- 1級の過去問(計算)解説
- 限定メルマガ
- わかる建築構造の用語集・図解集
- 1頁10円！PDF版の学習記事