HOME > 構造力学の基礎 > せん断力と曲げモーメントの関係、違いは？曲げモーメントからせん断力の求め方、せん断力図と曲げモーメント図の関係は？

【無料お試しキャンペーン中！】1級・2級建築士試験の構造の疑問を気軽に相談　初心者でもわかる！1級・2級建築士試験(構造)相談カフェ
管理人が業界分析！1日13円で建築業界がわかるLINE配信！　⇒　まずはリンクをクリックして友だち追加！

せん断力と曲げモーメントの関係、違いは？曲げモーメントからせん断力の求め方、せん断力図と曲げモーメント図の関係は？

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

せん断力は曲げモーメントの式を1階微分、曲げモーメントはせん断力を積分すると得られます。たとえば、曲げモーメントを求める式がPｘとします。Ｐは集中荷重、ｘは任意の長さです。このときせん断力は、Ｐｘをｘについて1階微分して「P」だと分かります。今回は、せん断力と曲げモーメントの関係、違いは、曲げモーメントからせん断力の求め方、せん断力図と曲げモーメント図の関係について説明します。曲げモーメント、せん断力の詳細は下記が参考になります。

曲げ応力とは？1分でわかる意味、公式と演習問題、単位、曲げ応力度との違い

【近日公開予定】せん断力とは？

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

せん断力と曲げモーメントの関係、違いは？

せん断力Qと曲げモーメントMには下式の関係があります。せん断力Qと曲げモーメントMは梁のスパン（長さ）ｘの関数で、曲げモーメントの関数を1階微分すると、せん断力の関数が得られます。

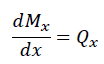
せん断力と曲げモーメントの関係

さらに、微分と積分は対の関係であり曲げモーメントを微分してせん断力が得られるなら「せん断力を積分すれば曲げモーメントとなる」ことが分かります。よって、上式について「梁のスパンxの微小長さdxとせん断力Qxの積」を全長xに渡り積分すると曲げモーメントMxが得られます。

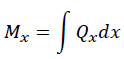
せん断力と曲げモーメントの関係2

前述したせん断力と曲げモーメントの関係は、計算だけでなく「せん断力図と曲げモーメント図の関係も同様」です。なお、せん断力と曲げモーメントの違いを下記に示します。

・せん断力　⇒　断面に平行に作用する1組のズレ合う力。四角形の物体にせん断力が作用すると平行四辺形に変形する

・曲げモーメント　⇒　断面を湾曲（回転）させようとする力。四角形の物体に曲げモーメントが作用すると上側と下側で「伸び、または、縮む」変形が起きる。そのため、曲げモーメントは引張力と圧縮力を組み合わせた力ともいえる。

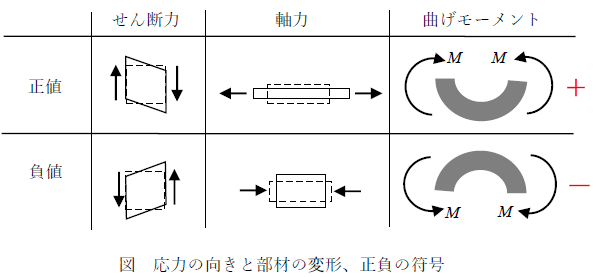
せん断力と曲げモーメントの関係、違い

さて、前述に示した曲げモーメントとせん断力の関係式を導出しましょう。下図に示すように、梁に任意の分布荷重が作用して力がつりあっているとします。このとき梁の微小部分を抜き出して応力のつりあいを考えましょう。微小部分の長さをdxとします。

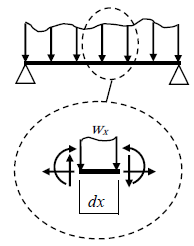
微小部分の応力

梁に作用する力はつりあっているのですから、微小部分においても力のつりあいは成立します。部材に生じる応力はせん断力、曲げモーメント、軸力の3つです。ただし、上図の梁には鉛直方向の荷重のみ作用するので軸力は0です。

以上より、梁の微小部分には下図のような応力および荷重が作用して力がつりあいます。

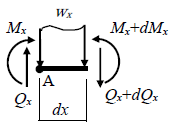
微小部分の力のつりあい

微小部分の右側では、分布荷重wxにより微小な応力が増加します。微小なせん断力、曲げモーメントをそれぞれdQx、dMx、左側のせん断力、曲げモーメントをQx、Mxとするとき

となります。鉛直方向の力のつりあいは

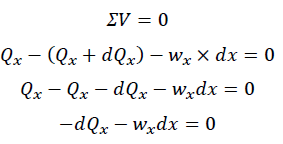
より

が得られます。上式より微小せん断力の大きさは、分布荷重と微小長さの積です。さらに両辺をdxで割ると

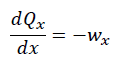
となり、上式はせん断力の1回微分したものが分布荷重になることを意味します。微分は関数の傾きを求めることに等しいので、せん断力の傾き（変化の割合）が分布荷重といえます。逆にいうと、部材に生じるせん断力が一定（あるいは0）の場合、分布荷重は作用していません。

次に点Aにおけるモーメントのつりあいを考えます。

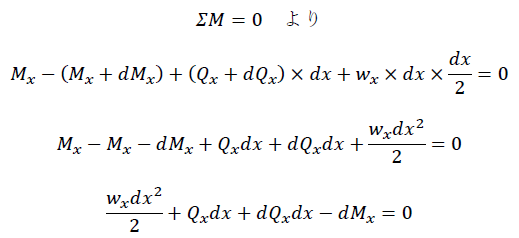
dx2、dQxdxは微小量の積のため無視できるくらい小さいと考えると

が求まります。上式より、微小曲げモーメントはせん断力と微小長さの積といえます。さらに両辺をdxで割ると

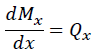
になります。上式は曲げモーメントの1回微分がせん断力になること、すなわち、曲げモーメントの変化の割合がせん断力といえます。せん断力と分布荷重の関係と同様に、曲げモーメントが一定の値（あるいは0）であればせん断力は0です。

さらに、

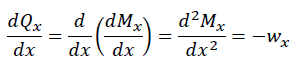
が求められます。上式より、曲げモーメントの２回微分が分布荷重と等しくなります。以上より、曲げモーメント、せん断力、荷重には下記の関係があります。

また、微分と積分は対の関係にあるので、1回積分すればせん断力、2回積分すれば曲げモーメントが求まることを意味します。つまり、せん断力、曲げモーメントはxの関数であり、分布荷重wxが作用するとき、xの増減に伴いQx、Mxも増減します。せん断力、曲げモーメントの詳細は下記が参考になります。

曲げ応力とは？1分でわかる意味、公式と演習問題、単位、曲げ応力度との違い

【近日公開予定】せん断力とは？

曲げモーメントからせん断力の求め方は？

曲げモーメントMからせん断力Qを求める方法を下記に示します。下式より、曲げモーメントの式を微分すればせん断力Qが得られます。

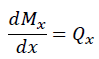
実際に下記の曲げモーメントをせん断力の式に変換しましょう。

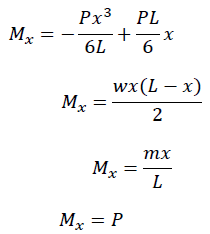
前述よりＭｘをｘについて微分すればよいので

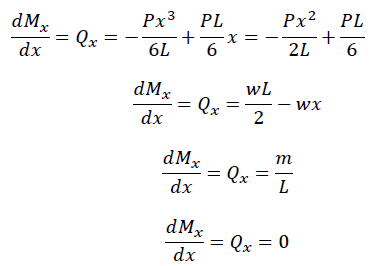
ですね。上記のように、Mxがxの関数を含まない定数（距離に関わらず一定の値）であれば、微分してゼロ、すなわちせん断力は0になります。

せん断力図と曲げモーメント図の関係は？

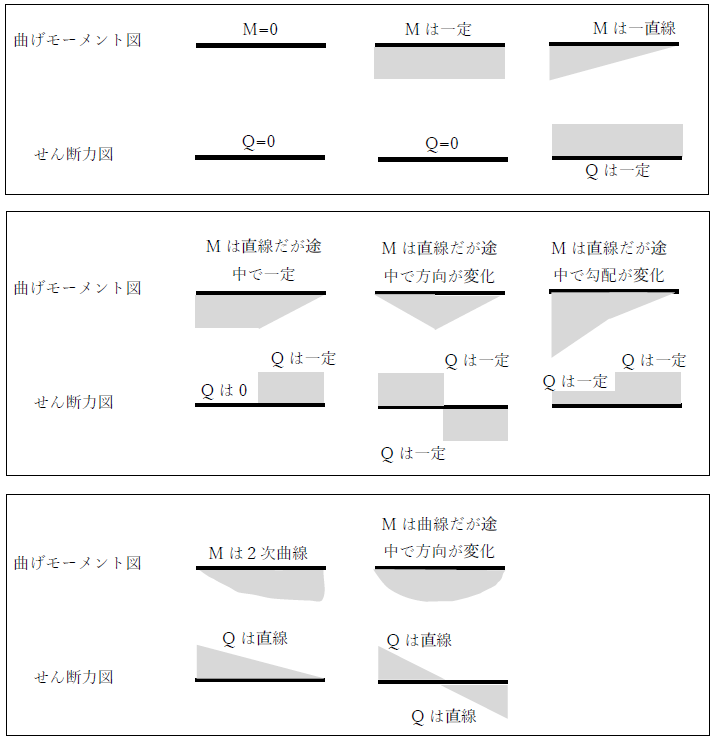
前述より、せん断力と曲げモーメントは相関関係にあるため、せん断力図と曲げモーメント図においても一定の法則があります。たとえば、曲げモーメントが2次関数であれば、微分して得られるせん断力は1次関数、曲げモーメントが1次関数の場合、せん断力は一定値、曲げモーメントが一定値であれば、せん断力は0です。これらの関係を覚えておけば、せん断力図と曲げモーメント図を描く際の手助けになるでしょう。

せん断力図と曲げモーメント図の関係