応力テンソルとは？1分でわかる意味、求め方、せん断応力と垂直応力の関係
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
応力テンソルとは、応力の成分を9方向に拡張した概念のことです。
これまで方向性を持たない量（スカラー）、量と方向をもつベクトルを勉強しました。
ベクトルにはx,y,zの方向がありますが、テンソルは6つの方向を加えて9方向に拡張します。今回は応力テンソルの意味、求め方、せん断応力と垂直応力の関係について説明します。
テンソル、スカラー、ベクトル、応力の意味は下記が参考になります。
応力テンソルとは？求め方
応力テンソルとは、応力の成分を9方向に拡張した概念です。構造力学では、基本的に平面の部材について考えました。そのため力の方向（成分）は2方向しかありません。
しかし実際には、部材は立体のためx,y,zの３方向あります。応力テンソルでは、立方体の各面内に沿った成分（6つの方向）+各面内に対して垂直の成分（3方向）の9方向に拡張した応力を考えます。
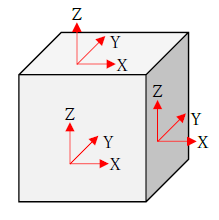
テンソルを納得するのは時間がかかるかもしれません。「そういうもの」と考えた方が楽です。あるいは、ベクトルで考慮できる成分（方向）を拡張（増やした）した概念と考えても大きく外してないでしょう。
テンソルの詳細、計算方法は下記が参考になります。
また応力の詳細は下記をご覧ください。
任意の物体に外力を加えました。内部に生じる内力は外力と釣り合い状態にあります。
このとき、物体内部の微小な面積要素ΔSを考え、この面の単位法線ベクトルnとします。
この内力を次の式で表します。
上式を応力ベクトルといいます。ここで、Tの頭にnという文字がついていますが、これは微小面積の向きすなわち、法線ベクトルのnの向きに応力ベクトルが依存するという意味です。
さて、物体に対して直角座標系xjをとるとき応力ベクトルは応力成分で示すことができます。よって
です。
また下図のようにx1軸に垂直な面を考えます。
初めに説明したように応力は法線ベクトルに依存しますので、
となります。以上のベクトルはx2, x3の場合も同様に考えることができますので、
です。i=1,2,3ですので
と表すことができます。上記のTjを応力テンソルといいます。前述したように、応力テンソルは9つの方向を持ちます。
応力の記号σを用いると、応力テンソルの式は
となります。この式でσijの、iはi軸に対する垂直な面を意味し、jは応力の方向を表しています。つまり、σ12であれば、｢x1軸に対する垂直な面に対してx2軸方向の応力｣という意味です。
応力テンソルとせん断応力、垂直応力の関係
上式で座表面に対して垂直な応力を｢垂直応力｣と言います。また、
など、座標面に沿って働くような面内に働く力をせん断応力と呼びます。
以上に示した式は数学的な表記方法ですが、私たちが一般的に使用しているのは工学的な書き方です。
構造力学で習ったような垂直応力やせん断応力はそれぞれ、σ22、σ12または、せん断応力はτxyと書きます。
まとめ
今回は応力テンソルについて説明しました。意味が理解頂けたと思います。
やや難解な概念ですが、応力を9つの成分に拡張した概念（考え方）と理解すれば良いでしょう。
さらに深く学習したい方はテンソル、応力の平衡方程式など勉強しましょうね。下記が参考になります。
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
▼スポンサーリンク▼
▼【好評！】管理人おすすめ▼
- あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！
▼用語の意味知らなくて大丈夫？▼
▼同じカテゴリの記事一覧▼
▼カテゴリ一覧▼
- 応力とひずみ(まずは、弾性と塑性の性質についてから)
- テンソルの計算(まずは、総和規約とはから)
- 応力やひずみの構成式(まずは、弾性材料についてから)
- 応力テンソル(まずは、応力テンソルから)
- ひずみテンソル(まずは、変形とひずみの式から)
- 2次元問題(まずは、平面応力状態と平面ひずみ状態から)
- 平板理論(まずは、キルヒホッフの仮説とは何か？から)
▼他の勉強がしたい方はこちら▼
【好評】LINEで質問！
管理人に質問してみる？
わかる1級建築士の計算問題解説書
【初回資料が今だけ無料！】1日約13円で情報をアップデート！
有料メルマガを無料で見てみませんか？⇒ 忙しい社会人、学生のためのビルディング・アップデート
わかる2級建築士の計算問題解説書！
【30%OFF】一級建築士対策も◎！構造がわかるお得な用語集
更新情報
- 当サイトでは、ほぼ毎日、記事更新・追加を行っております。
- 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。
- 新着記事一覧
プロフィール
- 略歴▼
- 名前 ハナダユキヒロ/MITUME lab代表.
- 2010年 弊サイトを開設
- 2010～2017年 国立大学大学院修了
- 2017年12月に当HPが書籍化。
- 「わかる構造力学」
- 2022年4月に「わかる構造力学」の改訂版出版。
- 「わかる構造力学(改訂版)」
- 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。
- 当サイトの目的▼
- 建築学生が学ぶ「構造力学」の目的
- とりあえず10記事▼
- 初めましての方に10記事用意しました
- おすすめ書籍紹介▼
- ハナダユキヒロが建築関連書籍の良書を選びました
建築の本、紹介します。▼
▼【好評！】管理人おすすめ▼
- あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！
- HOME > 材料力学の基礎 > 応力テンソルとは？1分でわかる意味、求め方、せん断応力と垂直応力の関係
- 1級の過去問(計算)解説
- 限定メルマガ
- わかる建築構造の用語集・図解集
- 1頁10円！PDF版の学習記事