- 【無料お試しキャンペーン中！】1級・2級建築士試験の構造の疑問を気軽に相談 初心者でもわかる！1級・2級建築士試験(構造)相談カフェ
- 管理人が業界分析！1日13円で建築業界がわかるLINE配信！ ⇒ まずはリンクをクリックして友だち追加！
一次元圧密とは？1分でわかる意味、テルツァーギの圧密方程式とは？
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
一次元圧密とは、地盤の深さ方向（1次元）の変化のみ考える圧密です。土をはじめ、実際の物体は三次元（立体）ですが、次元を減らすことで扱う情報量（変数）を省略し、比較的簡単な計算式が得られます。ただし、次元を減らす（変数を減らす）ために、多くの仮定が必要となり、すなわち、適用範囲が狭くなります。今回は、一次元圧密の意味、テルツァーギの圧密方程式について説明します。圧密の詳細、テルツァーギの圧密方程式の誘導は下記が参考になります。
テルツァーギの圧密理論とは？一次元圧密の基礎方程式の誘導方法は？
100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒ いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事
一次元圧密とは？
一次元圧密とは、地盤の深さ方向（1次元）の変化のみ考える圧密です。実際の土（および物体）は３次元（立体）ですが、次元が多くなるほど情報量（変数）が多く、計算が面倒になります。そこで次元を減らして変数を省略することで、比較的簡単な計算式が得られます。
この操作は圧密だけではなく、たとえば、構造力学における初等梁理論でも同様に「1方向の変化のみ」考えます。
一方で、次元を減らすために多くの仮定が必要となり、すなわち、得られた計算式の適用範囲は限られる点に注意しましょう。
さて、一次元圧密の理論はテルツァーギにより考えられました。この圧密のモデルはシンプルかつ巧妙です。ここで簡単に解説します。テルツァーギの圧密進行モデルは「ピストン、バネ」で説明されます。
下図に示すようにピストンの筒、細かな孔の空いた蓋、それを繋ぐバネ（かたさをもつバネ）を考えます。このときピストンの容器は水で満たされています。
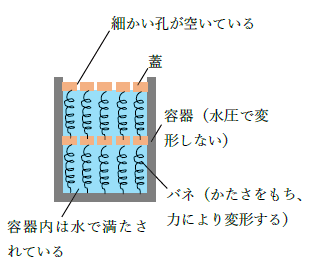
バネは土粒子の骨格、水は土の間隙水を表しています。また、ピストンの蓋に細かな孔があるのは「粘性土の透水性」を表します。粘性土は粒子が細かく透水性の低い土のため、細かな孔を空けています。
上図のピストンに圧力が作用すると、載荷直後はバネは変形しませんが、時間の経過と共にバネは変形し（圧密が進行）、次第にバネの変形が終了（圧密終了）します。この現象を荷重（圧力）Δp、全応力Δσ、有効応力Δσ'、過剰間隙水圧Δuから考えましょう。
過剰間隙水圧とは？1分でわかる意味、求め方、読み方、間隙水圧との違いは？
全応力とは？1分でわかる意味、求め方、有効応力との違い、間隙水圧の求め方は？
まず、圧力を載荷した直後（圧密直後）は、透水性が低いために孔から水は溢れず、バネも変形しません。言い換えると、圧力Δpは水圧と釣り合っているのであり、このΔpと釣り合う水圧Δu（Δp＝Δu）は、静水圧を超えておりこれを「過剰間隙水圧（Δu）」といいます。
時間が経過すると孔から水が溢れバネが少しずつ変形します。バネが変形するということは、フックの法則（p=kδ）より、バネに応力（有効応力）が生じていることを意味します。同時に、過剰間隙水圧は減少しており、この減少分の過剰間隙水圧がバネに伝達されたことが分かります。
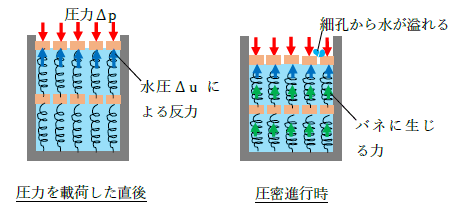
さらに時間が経過するとバネの変形が止まります（バネが静止する）。これは圧力Δpとバネに生じる有効応力Δσ'が釣り合っている（Δp＝Δσ'）ことを意味し、一方で、過剰間隙水圧は0になります。
以上について、圧力Δpおよび応力の関係を整理すると
・t＝0（圧力載荷直後） ⇒ Δu＝Δp、Δσ'＝0、Δσ＝Δu+Δσ'＝Δp
・t＝ta（圧密進行中） ⇒ Δu＝Δua、Δσ'＝Δp－Δua、Δσ＝Δu+Δσ'＝Δp
・t＝max（圧密終了） ⇒ Δu＝0、Δσ'＝Δp、Δσ＝Δu+Δσ'＝Δp
になります。圧密の考え方は下記もご覧ください。
テルツァーギの圧密方程式とは？
前述の圧密モデルについて、複数の仮定に基づき、テルツァーギは圧密進行の偏微分方程式を導きました。これをテルツァーギの圧密方程式（一次元圧密の基礎方程式）といいます。圧密方程式を下記に示します。なお、c vを圧密係数といいます。
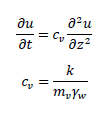
uは任意の間隙水圧、tは任意の時間、zは任意の高さ、kは透水係数、mvは体積圧縮係数、γwは水の密度です。上式は偏微分方程式であり、境界条件を設定し解が算定できます。圧密係数、テルツァーギの圧密方程式の誘導方法は下記が参考になります。
テルツァーギの圧密理論とは？一次元圧密の基礎方程式の誘導方法は？
まとめ
今回は一次元圧密について説明しました。一次元圧密とは、地盤の深さ方向（一方向）の変化のみ考えた圧密です。一次元圧密はテルツァーギにより圧密進行のモデルおよび理論式が導かれました。圧密の意味、圧密方程式の求め方など下記も参考になります。
テルツァーギの圧密理論とは？一次元圧密の基礎方程式の誘導方法は？
【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）
▼人気の記事ベスト３▼
- 1.断面係数の計算方法を本当にわかっていますか？→断面係数とは？
- 2.丸暗記で良いと思ったら大間違い→断面二次モーメントとは何か？
- 3.違いを適切に説明できますか？→等分布荷重とは？集中荷重との違いや使い方について
▼用語の意味知らなくて大丈夫？▼
▼同じカテゴリの記事一覧▼
- 圧密試験とは？1分でわかる意味、方法、透水係数、粘性土との関係
- 圧密度とは？1分でわかる意味、求め方、単位、圧密度90、100の意味、時間係数との関係は？
- ダルシーの法則とは？1分でわかる意味と公式、透水係数、流量との関係は？
- 有効応力の基礎知識と、よくわかる全応力との違い
- 全応力とは？1分でわかる意味、求め方、有効応力との違い、間隙水圧の求め方は？
- 間隙水圧の基礎知識、有効応力との関係
- 過剰間隙水圧とは？1分でわかる意味、求め方、読み方、間隙水圧との違いは？
- 圧密降伏応力の基礎知識と、土の変形について
▼カテゴリ一覧▼
- 基礎構造の用語(まずは、土圧ってなに？良く分かる土圧の算定方法や土圧の種類から)
- 地盤の強さを学ぶ(まずは、基礎、N値、支持層から)
- 基礎構造その他(まずは、建築基準法にみる「木造の構造方法」のＴＩＰＳから)
- 基礎構造の種類(まずは、直接基礎と杭基礎から)
- 直接基礎の計算(まずは、独立基礎の設計概要から)
- 杭の計算(まずは、杭の種類はどのくらい？設計者が教える杭の種類と各杭の特徴、施工方法から)
- 地盤の性質を学ぶ(まずは、地盤調査の結果、砂層が安全？粘土層が危険は本当か？から)
▼他の勉強がしたい方はこちら▼
【読まれています】管理人による建築業界の分析！
1日13円で建築業界がわかるLINE配信！。
わかる1級建築士の計算問題解説書
あなたは数学が苦手ですか？
【有料メルマガの初回資料が今だけ無料！】1日約13円で情報をアップデート！
有料メルマガを無料で見てみませんか？⇒ 忙しい社会人、学生のためのビルディング・アップデート
わかる2級建築士の計算問題解説書！
【30%OFF】一級建築士対策も◎！構造がわかるお得な用語集
更新情報
- 当サイトでは、ほぼ毎日、記事更新・追加を行っております。
- 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。
- 新着記事一覧
プロフィール
- 略歴▼
- 名前 ハナダユキヒロ/MITUME lab主宰.（筆者のコラムはこちら）
- 2010年 弊サイトを開設
- 2010～2017年 国立大学大学院修了
- 2017年12月に当HPが書籍化。
- 「わかる構造力学」
- 2022年4月に「わかる構造力学」の改訂版出版。
- 「わかる構造力学(改訂版)」
- 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。
- 自己紹介▼
- 建築学生が学ぶ「構造力学」とは？
- とりあえず10記事▼
- 初めましての方に10記事用意しました
- おすすめ書籍紹介▼
- ハナダユキヒロが建築関連書籍の良書を選びました
建築の本、紹介します。▼
同じカテゴリの記事一覧
- HOME > 基礎構造を学ぶ > 一次元圧密とは？1分でわかる意味、テルツァーギの圧密方程式とは？
- 1級の過去問(計算)解説
- 限定メルマガ
- わかる建築構造の用語集・図解集
- 1頁10円！PDF版の学習記事