1. HOME > 数学の基礎 >3つの分数の通分は？1分でわかる計算方法、3つの分数の掛け算、例題

3つの分数の通分は？1分でわかる計算方法、3つの分数の掛け算、例題

3つの分数の通分は「３つの分数の分母が等しくなるような数」を、各分数の分子と分母に掛け算します。考え方は「２つの分数の通分」と同じです。例として「1/2+1/3+1/4」を通分して和を求めましょう。３つの分母に共通する倍数を見つければよいです。例えば「2×3×4＝24」は共通する倍数の１つです。分母が24になるように各分数の分子と分母に掛け算すると「1/2+1/3+1/4=12/24+8/24+6/24＝(12+8+6)/24=26/24=13/12」です。

今回は、3つの分数の通分の計算方法、3つの分数の掛け算、例題について説明します。通分、最小公倍数の詳細は下記が参考になります。

通分とは？1分でわかる意味、足し算と引き算の問題、最小公倍数との関係

最小公倍数とは？1分でわかる意味、求め方と計算、最大公約数との違い

管理人おすすめ書籍⇒　見るだけで理解が加速する　得点アップ　数学公式図鑑 [ あきとんとん ]

3つの分数の通分は？計算方法と例題

3つの分数の通分は「3つの分数の分母が等しくなるような数」を、各分数の分子と分母に掛け算します。考え方は「２つの分数の通分」と同じです。ただし、異なる分数が３つになるので、計算が面倒になります。※通分の考え方は下記をご覧ください。

通分とは？1分でわかる意味、足し算と引き算の問題、最小公倍数との関係

例題として下記の3つの分数を通分し和を求めてください。

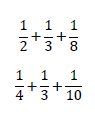
3つの分数の分母を等しくするためには、３つの分母に共通する倍数を見つければよいです。共通する倍数は「できるだけ小さい値」を見つけた方が計算は簡単です。これを「最小公倍数」ともいいます。

ちなみに、共通する倍数を簡単に見つける方法は「３つの分母の掛け算」です。例えば「1/2+1/3+1/4」の分母を等しくするなら「2×3×4＝24」を分母にすればよいのです。

よって「1/2+1/3+1/8」の場合、分母は「2×3×8＝48」、「1/4+1/3+1/10」では「4×3×10＝120」です。よって、

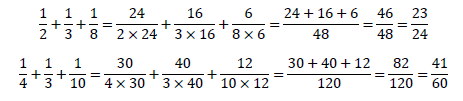
です。通分と足し算、最小公倍数の求め方は下記が参考になります。

通分と足し算の関係は？1分でわかる意味、分数の足し算の問題と計算

最小公倍数とは？1分でわかる意味、求め方と計算、最大公約数との違い

3つの分数の掛け算は？

分数の掛け算は「分数の足し算」より考え方は簡単です。分数の掛け算では「分子同士、分母同士で掛け算」すればよいです。例として、下記の3つの分数の掛け算を計算します。

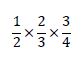
答えは下記の通りです。また、単に掛け算するだけでなく「約分」をして、できるだけ簡単な形で表しましょう。

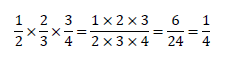
分数の掛け算、約分の詳細は下記が参考になります。

整数×分数のやり方は？1分でわかる計算、割り算の仕方、問題の解き方

約分とは？1分でわかる意味、やり方、問題、約数、素因数分解との関係

管理人おすすめ書籍⇒　見るだけで理解が加速する　得点アップ　数学公式図鑑 [ あきとんとん ]

まとめ

今回は、3つの分数の通分について説明しました。3つの分数の通分は「３つの分母が等しくなるような数を、各分数の分子と分母に掛け算」します。考え方は２つの分数の通分と同じです。ただし計算が面倒になるのでケアレスミスに注意しましょう。通分の詳細など下記も参考になります。

通分とは？1分でわかる意味、足し算と引き算の問題、最小公倍数との関係

分数の足し算は？3分でわかる計算、問題、分母が同じ場合、通分の計算

最小公倍数とは？1分でわかる意味、求め方と計算、最大公約数との違い

管理人おすすめ書籍⇒　増補改訂版　中学校3年分の数学が教えられるほどよくわかる [ 小杉 拓也 ]

▼スポンサーリンク▼

更新情報

• 当サイトでは、ほぼ毎日、記事更新・追加を行っております。


• 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。


• 新着記事一覧

プロフィール

• 
• 略歴▼
• 名前　ハナダユキヒロ/MITUME lab代表.
• 2010年　弊サイトを開設
• 2010～2017年　国立大学大学院修了
• 2017年12月に当HPが書籍化。
• 「わかる構造力学」
• 2022年4月に「わかる構造力学」の改訂版出版。
• 「わかる構造力学(改訂版)」


• 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。


• 当サイトの目的▼
• 建築学生が学ぶ「構造力学」の目的


• とりあえず10記事▼
• 初めましての方に10記事用意しました


• おすすめ書籍紹介▼
• ハナダユキヒロが建築関連書籍の良書を選びました

建築の本、紹介します。▼

同じカテゴリの記事一覧

• 分数とは？1分でわかる意味、分母、分子、約分、掛け算と割り算の解き方
• 数学の分子とは？1分でわかる意味、分母、0との関係、分母と分子を入れ替える計算
• 分母とは？1分でわかる意味、分子、有理
• 既約分数とは？1分でわかる意味、定義、既約分数式、公約数、2と5の関係
• 約分とは？1分でわかる意味、やり方、問題、約数、素因数分解との関係
• 約分と通分の違いは？1分でわかる意味、計算のコツ
• 有理式とは？1分でわかる意味、例、計算、分数式との関係
• 分数式とは？1分でわかる意味、約分、通分の計算、足し算の方法と問題
• 部分分数とは？1分でわかる意味、分解の計算（やり方）、恒等式との関係
• 分数の2乗とは？1分でわかる意味、計算、書き方、√との関係