1. HOME > 構造計算の基礎 > 弧度法とは？1分でわかる意味と考え方、読み方、定義、公式、変換

弧度法とは？1分でわかる意味と考え方、読み方、定義、公式、変換

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

弧度法（こどほう）とは、弧度(＝57.3°)を1ラジアンとして角度の単位を表す方法です。弧度法で角度をあらわす公式はθ＝L／ｒです。Lは円弧の長さ、ｒは円の半径です。弧度法は、数学的に扱いやすいメリットがあります。一方で日常生活では度数法（360°が円の角度）が一般的です。弧度法と度数法の関係も理解すべきでしょう。今回は弧度法の意味と考え方、読み方、定義、公式、変換について説明します。弧度の意味は、下記が参考になります。

弧度とは？1分でわかる意味、読み方、ラジアン、角度との関係

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

記事を書いた人

ハナダユキヒロ／建築学生が学ぶ「構造力学」

難解な構造力学、建築構造の用語を分かりやすく解説する専門家。高等専門学校在学中から建築学生が学ぶ「構造力学」を運営。その後、国立大学大学院⇒組織設計事務所⇒弊サイト運営に従事している。

著書：「わかる構造力学/工学社」、「わかる構造力学 改訂版/工学社」

LINEで質問したい方はこちら　⇒　【好評】管理人にLINEで質問してみよう

弧度法とは？

弧度法とは、弧度（＝57.3°）を1ラジアンとして角度の単位を表す方法です。なお、57.3°＝180／πです。弧度の求め方は下記が参考になります。

弧度とは？1分でわかる意味、読み方、ラジアン、角度との関係

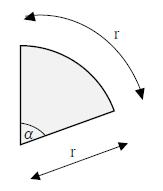
まず、左下図をみてください。半径ｒ、弧長がｒのとき角度α＝57.3°(180/π)になります。αを弧度といいます。次に右下図をご覧ください。57.3°を1(rad)としました。これが弧度法です。

弧度法は、度数法よりも数学的に扱いやすいメリットがあります。度数法だと72°という半端な数値も、弧度法では2π/5という簡単な値に変換できます。

弧度は57.3°ですが、この値を基準に考えると数値が半端になります。そこで弧度法は、180/π＝1radを基準に考え角度を表します。

弧度法の読み方

弧度法は「こどほう」と読みます。関係用語の読み方は下記です。

弧度　⇒　こど

度数法　⇒　どすうほう

弧度の意味は、下記が参考になります。

弧度とは？1分でわかる意味、読み方、ラジアン、角度との関係

弧度法の定義

弧度法の定義は下記です。

弧度を1ラジアン(rad)として角度を表す方法。弧度＝57.3°(又は180/π)で表す。

弧度法と角度の公式

弧度法による角度の公式は下記です。

θ＝L／r

θは角度で単位はラジアン、Lは円弧の長さ、ｒは半径です。円弧の長さ、半径も単位は同じです。よって無次元数となり単位は省略することが多いです。便宜的にradを付けることもあります。

下図をみてください。円弧の長さL、角度をθ、半径をｒとします。角度が何ラジアンになるか計算しましょう。

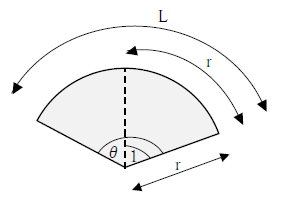
1ラジアンに対する角度θの比率と、円弧の長さの比率が同じになることを利用します。

θ：1＝L：ｒ

θ×ｒ＝L

θ＝L／ｒ

ですね。

弧度法では、角度を円弧の長さと半径の長さから計算できます。簡単な計算で角度を算定できるのは大きなメリットですね。

弧度法、度数法の変換

大きなメリットのある弧度法ですが、一般的に使う機会は少ないです。また、度数法の方がよく利用されるため、弧度法と度数法の変換は必ず理解すべきでしょう。弧度法と度数法の変換の公式を示します。

弧度法　⇒　度数法への変換公式

α＝180/π×θ

※θはラジアン、αは「°」とする。

度数法　⇒　弧度法への変換公式

θ＝π/180×α

※θはラジアン、αは「°」とする。

πが付くので難しそうな式ですが、そんなことは無いです。元々、弧度は57.3°でしたね。小数点が嫌なので180/πで表しています。さて、57.3°＝1radです。よって60°を弧度法で表すと、

60÷57.3＝1.047rad

です。57.3が1なので、少し大きな60°は1より少しだけ大きい値です。前述した公式は上記の計算と同じことです。但し、57.3°は面倒な数字なので、180/πを使っています。

60÷180/π＝60×π/180＝π/3≒1.047

です。

最後に弧度法から度数法への変換も練習しましょう。2π/7を度数法で表してください。前述した公式に当てはめれば簡単ですね。

α＝180/π×2π/7＝360/7＝51.4°

です。

下記も参考になります。

ラジアンから角度への変換は？1分でわかる求め方、式、計算ツール

まとめ

今回は弧度法について説明しました。意味が理解頂けたと思います。弧度法は、弧度(180/π)を1ラジアンとして角度を表す方法です。数学的に扱いやすいメリットがあります（計算が簡単）。とはいえ、度数表示を使うことも多いので弧度法から度数法への変換も理解しましょう。弧度の意味は、下記も参考になります。

弧度とは？1分でわかる意味、読み方、ラジアン、角度との関係

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

▼スポンサーリンク▼

【初回資料が今だけ無料！】1日約13円で情報をアップデート！

有料メルマガを無料で見てみませんか？⇒　忙しい社会人、学生のためのビルディング・アップデート

更新情報

• 当サイトでは、ほぼ毎日、記事更新・追加を行っております。


• 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。


• 新着記事一覧

プロフィール

• 
• 略歴▼
• 名前　ハナダユキヒロ/MITUME lab代表.
• 2010年　弊サイトを開設
• 2010～2017年　国立大学大学院修了
• 2017年12月に当HPが書籍化。
• 「わかる構造力学」
• 2022年4月に「わかる構造力学」の改訂版出版。
• 「わかる構造力学(改訂版)」


• 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。


• 当サイトの目的▼
• 建築学生が学ぶ「構造力学」の目的


• とりあえず10記事▼
• 初めましての方に10記事用意しました


• おすすめ書籍紹介▼
• ハナダユキヒロが建築関連書籍の良書を選びました

建築の本、紹介します。▼

▼【好評！】管理人おすすめ▼

• あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！

同じカテゴリの記事一覧

• 弧度とは？1分でわかる意味、読み方、ラジアン、角度との関係
• ラジアンから角度への変換は？1分でわかる求め方、式、計算ツール
• 傾斜の計算とは？1分でわかる意味、勾配の高さ、長さ、角度の計算
• 100分の1勾配とは？1分でわかる意味、1/100勾配の計算、角度の求め方
• 勾配の1/50とは？1分でわかる意味、1/100、1/12、1:2の角度と計算方法
• 勾配の1：2とは？1分でわかる意味、計算、1/100、1/12、表記との関係
• 勾配の計算は？1分でわかる意味、単位、パーセント、1/100、20パーセントの関係
• 勾配の角度表は？1分でわかる角度表、勾配との関係、屋根勾配3/100の角度
• 法面とは？1分でわかる意味、読み方、勾配、計算方法、建築物との関係
• 屋根勾配とは？1分でわかる意味、計算、角度、3寸
• 建築で数学は必要？現役設計者が教える必要な公式、範囲、物理との関係