1. HOME > 構造計算の基礎 > 層間変形角とは？層間変位の計算・1/200の制限を図解で解説

層間変形角とは？層間変位の計算・1/200の制限を図解で解説

【管理人おすすめ！】セットで3割もお得！約1,100語の用語集＋476点の図解集セット⇒　建築構造がわかる基礎用語集＆図解集セット

層間変形角は、「各階の高さｈに対する各階の層間変位δとの割合」です。建築基準法施行令第82条の2に定義されます。

層間変位をδ、各階の高さをｈとするとき、層間変形角は下式で求めます。

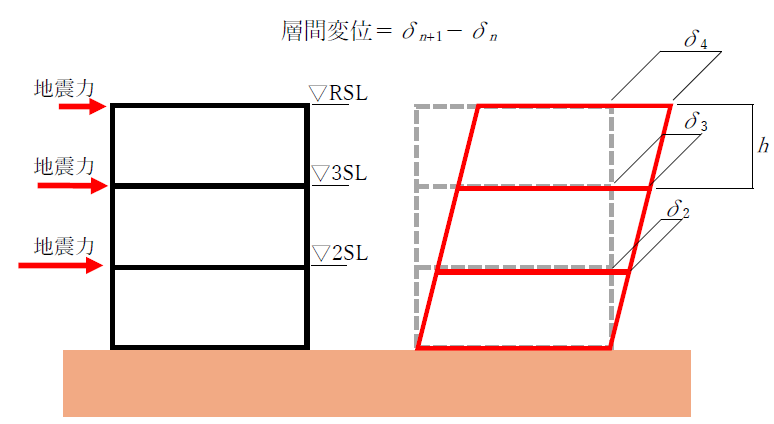
層間変形角をみれば、地震力による各階の変形度合い（どの程度、変形が大きいのか）が一目でわかります。

私は日々、構造設計する中で「層間変形角」は当たり前に計算しています。今回は、層間変形角や層間変位の意味を図解でわかりやすく解説します。

層間変形角とは？

層間変形角は、「各階の高さｈに対する各階の層間変位δとの割合」です。建築基準法施行令第82条の2に定義されます。

層間変形角と聞くと難しそうですが考え方は簡単です。

要するに、地震力による各階の変形度合いを示しているのです。

層間変形角の計算式も単純ですが、層間変位の意味、各階の高さのとり方を適切に理解する必要があるので後述します。

さて、層間変位をδ、各階の高さをｈとするとき、層間変形角は下式で求めます。

上式の通り、層間変形角は「分数の値で表示」します。

たとえば、階高が3000mm、層間変位が10mmの場合、層間変形角は

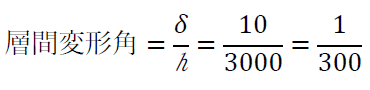
1/300になります。

上式より、層間変位δが大きいほど層間変形角も大きい値（分母が小さく）なり、δが小さいほど層間変形角も小さく（分母が大きく）なります。

層間変形角は階高と変位との割合なので、真に、各階の変形のしにくさが明らかになります。

たとえば、階高6000mmに対して層間変位10ｍｍと、階高3500mmに対して層間変位5ｍｍでは、一見、前者の方が大きく変形しているようにみえます。

しかし、これは見かけ上大きく見えているだけで層間変形角を計算すれば、本当はどちらが『変形しにくい建物か』分かるのです。

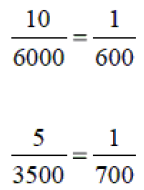
上記の例では、分母の大きい後者の方が変形しにくい構造といえます。層間変形角では、分母の数字がより大きいほど変形しにくいことを意味します。

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

層間変形角の制限

それではなぜ、層間変形角を求める必要があるのでしょうか。これは建築基準法施行令による

• 構造規定による層間変形角の制限（令82条の2）
• 防火避難規定のによる層間変形角の制限（令第109条の2の2）

の制限のためです。２は防火上の規定のため解説を省略し、構造上の規定である令82条の2の制限を詳しく解説します。

令82条の2を下記に引用します。

（層間変形角）令82条の2 建築物の地上部分については、第88条第1項に規定する地震力(以下この款において「地震力」という。)によって各階に生ずる水平方向の層間変位を国土交通大臣が定める方法により計算し、当該層間変位の当該各階の高さに対する割合(第82条の6第二号イ及び第109条の2の2において「層間変形角」という。)が1/200(地震力による構造耐力上主要な部分の変形によつて建築物の部分に著しい損傷が生ずるおそれのない場合にあっては、1/120)以内であることを確かめなければならない。

令82条の2では、層間変形角は1/200以内とする制限があります（※１帳壁、内・外装材、設備等に著しい損傷が生じるおそれのない場合）。

上記の層間変形角の制限は

外装材、内装材（仕上げ材）などの脱落（剥落）防止、帳壁、設備等の著しい損傷の防止

のために規定されます。

勘違いされがちですが、層間変形角を1/200以内に抑える制限は構造部材のためではなく、仕上げ材や帳壁、設備などのいわゆる非構造部材のための規定です。

構造部材は地震力による変形にも耐えられる設計がされています。

ところが、外装材や内装材などの非構造部材では、地震力による大きな変形に追従できる性能が無いため脱落（剥落）する恐れがあります。

そこで、構造設計により層間変形角の制限をすることで、外装材・内装材などの脱落を防止するようにします。

逆にいうと、外装材、内装材（仕上げ材）、帳壁、設備等に著しい損傷が無いことが確認できれば、層間変形角の制限を1/120まで緩和できます。

上記の※１が確認できる工法として

• 金属板
• ボード類その他これに類する材料仕上げ
• ALCパネルを用いた場合、縦型ロッキング工法、横壁カバープレート工法、縦壁スライド工法

があります。

層間変位の計算方法

層間変位の計算方法は

です。δnはn層（層は床の位置）の水平変位量、δn+1はn層より1つ上の層（床）における水平変位量です。

層間変位の計算方法の定義は平19国交告第594号第3に規定されています。

告示594号（平19国交告第594号第3） 第3　地震力によって各階に生ずる水平方向の層間変位の計算方法 第一号　令第82条の2に規定する層間変位は、地震力が作用する場合における各階の上下の床版と壁又は柱とが接する部分の水平方向の変位の差の計算しようとする方向の成分として計算するものとする。この場合において、同条に規定する層間変形角（当該層間変位の当該各階の高さに対する割合をいう。）については、上下の床版に接する壁及び柱のすべてについて確かめなければならない。 第二号　前号の規定にかかわらず、令第82条の6第二号イの規定に従って剛性率を計算する場合における層間変形角の算定に用いる層間変位は、各階において当該階が計算しようとする方向のせん断力に対して一様に変形するものとして計算した水平剛性の数値に基づき計算するものとする。ただし、特別な調査又は研究によって建築物の層間変位を計算した場合にあっては、この限りでない。

一言でいうと、層間変位は建物の床（層）から床までの相対的な水平変位量です。

単に「変位」と書いてあれば良いのですが、「層間」と書いてあることに着目します。これは図をみた方がわかりやすいでしょう。

下図は3階建ての建物が地震によって変形した図です。破線が変形前の建物と考えてください。このとき、１階床は変形しませんが、２階～屋根まで変形が生じています。

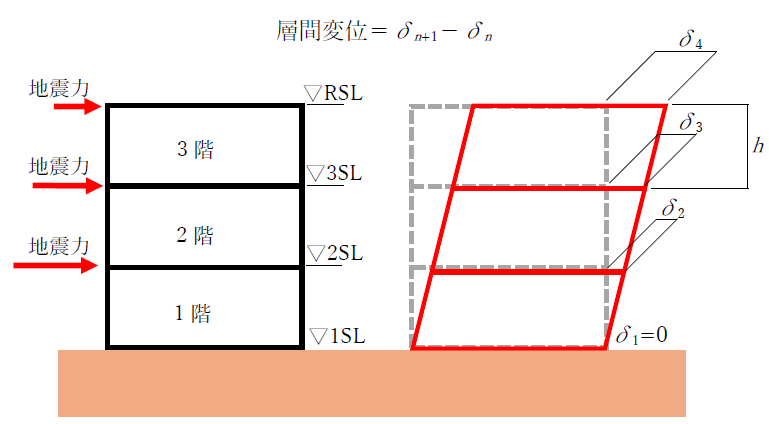
よって、各層での水平変位量の差をとることで、各階に生じる水平変位量がわかるのです。

上図の例を元に、層間変位を計算しましょう。

2階の層間変位は、2階床（2層の位置）における水平変位量δ2と、その上の床（3層の位置）の水平変位量δ3の差です。よって

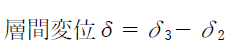
です。

余談になりますが、地震の揺れで最も水平変位が大きくなる階は最上階ですが、これは、１階から最上階までの水平変位が累積された結果です。

層間変位を計算すると必ずしも最上階の値が最大になるとは限りません。

階の高さhのとりかた

層間変形角の算定でもう１つ重要な要素が「階の高さ」です。いわゆる階高とはやや取り扱いが異なるため、あえて「階の高さ」と明記しています。

層間変形角の計算に用いる階の高さhは下記とします。

階の高さは原則として、層間変形角を計算する鉛直部材の当該階の床版上面位置から上階の床版上面位置までの鉛直距離を用いる。

要するに、当該階のスラブ天端から上階のスラブ天端までの距離を階の高さとします。

下図に階の高さのとり方を示しました。

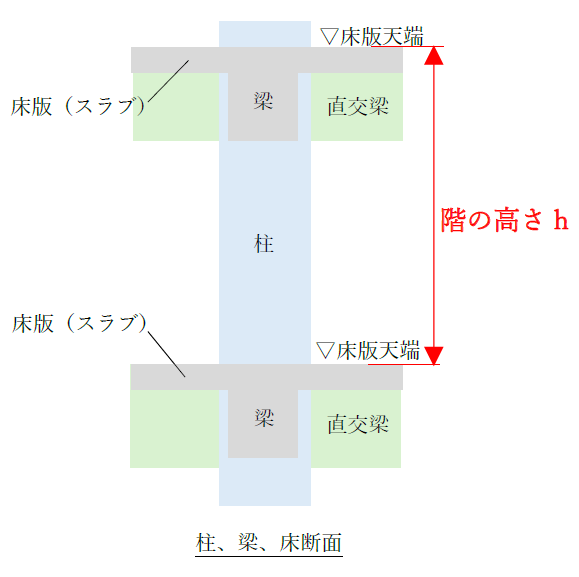
スラブから上のスラブまでの距離と考えれば簡単ですね。

はじめて層間変形角の学習をする方は疑問に思わないかもしれませんが、実は、構造設計を知っている方にとっては、上記の階の高さのとり方は、むしろ違和感を覚えるでしょう。

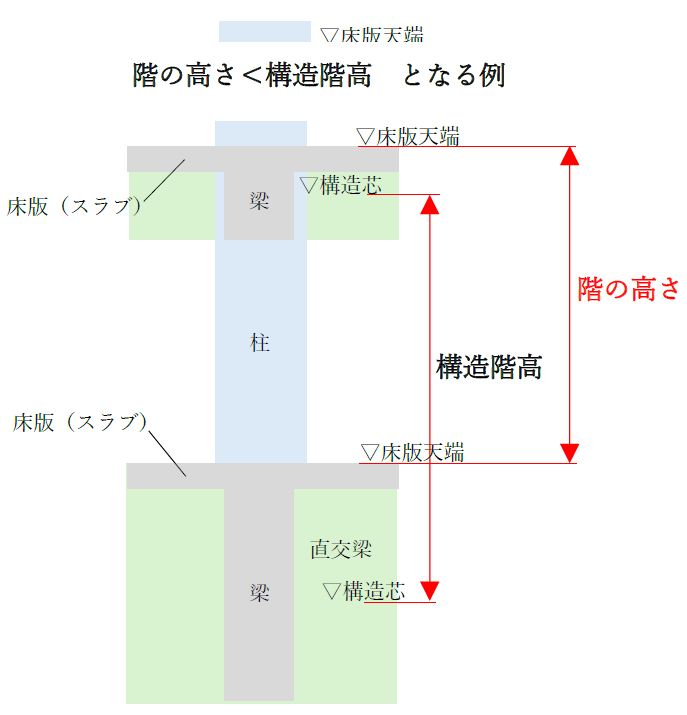
というのも、通常、構造設計における階の高さは、いわゆる構造階高といい、構造躯体の芯間距離（おおむね、大梁の中心から上階大梁の中心までの距離）とするからです。

階高とは？どこからどこまで？構造階高・天井高との違いをわかりやすく解説

ではなぜ、層間変形角の階の高さは「床天端から床天端までの距離」とするのでしょうか。

これは、階の高さを構造階高にすると、ある階の床梁せいが非常に大きい場合（基礎梁など）に、階の高さを過大評価する恐れがあるためです。

階の高さを過大評価することは、言い換えると、層間変形角を過小評価することになります。

層間変形角を過小評価することは、簡単にいうと、変形を小さく見積もることに等しいので許されませんね。

また、逆ばりとなって梁天端と床天端が一致しない場合、吹き抜けにより床版が無い場合には

・床版上面位置の代わりに梁の上面位置を用いる

ことにします。下図に示しました。

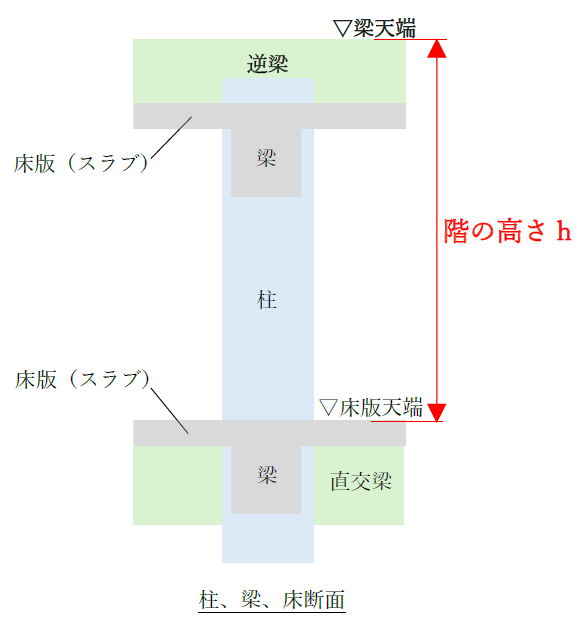
階高の意味は下記が参考になります。

階高とは？どこからどこまで？構造階高・天井高との違いをわかりやすく解説

層間変形角の制限が適用される建物

最後にこれまで解説した層間変形角の制限が適用される建築物を示します。

層間変形角の制限が適用されるのは

・構造計算ルート2

・構造計算ルート3

の耐震計算ルートをとる規模の建築物です。詳細な規定はありますが、概ね、中規模以上の建築物と考えれば良いでしょう。

なお、小規模の建築物の耐震計算ルートである構造計算ルート1は、層間変形角の制限は適用されません。

構造計算ルートとは何か？

層間変形角の基本事項を整理した表を示します。

項目	内容	備考
層間変形角の定義	層間変位δを各階の高さhで割った値（δ/h）	令82条の2に定義
制限値	1/200以内（非構造部材の損傷防止）	緩和条件により1/120まで可
階の高さhのとり方	スラブ天端から上階スラブ天端までの距離	構造階高とは異なる

まとめ

今回は、層間変形角や層間変位、階の高さのとり方について説明しました。層間変位は各層の変位差を意味します。層間変形角は層間変位と階の高さとの割合です。

建築基準法施行令第82条の2に定義されており、層間変位をδ、各階の高さをｈとするとき、層間変形角は下式で求めます。

また層間変形角は、保有水平耐力の算定にも用います。ある層間変形角に達した時を建物の耐力とするのです。下記も併せて学習しましょう。

保有水平耐力とは？意味・計算・必要保有水平耐力との違い

必要保有水平耐力とは？算定式Qun=Ds×Fes×Qud・Ds・Fesの意味

【管理人おすすめ！】セットで3割もお得！約1,100語の用語集＋476点の図解集セット⇒　建築構造がわかる基礎用語集＆図解集セット

プロフィール

• 
• 略歴▼
• 名前　ハナダユキヒロ/ミツメラボ代表.
• 2010年　弊サイトを開設
• 2010～2017年　国立大学大学院修了
• 2017年12月に当HPが書籍化。
• 「わかる構造力学」
• 2022年4月に「わかる構造力学」の改訂版出版。
• 「わかる構造力学(改訂版)」


• 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。


• 当サイトの目的▼
• 建築学生が学ぶ「構造力学」の目的


• とりあえず10記事▼
• 初めましての方に10記事用意しました


• おすすめ書籍紹介▼
• 構造力学・建築構造のおすすめ本｜現役設計者が読んで良かった書籍を紹介

建築の本、紹介します。▼

同じカテゴリの記事一覧

• 安全限界とは？意味・読み方と損傷限界・使用限界・層間変形角の関係
• 一次設計とは？1分でわかる意味、震度との関係、二次設計との違い
• 二次設計とは？一次設計との違い・対象建物の条件と保有水平耐力計算の流れ
• 構造計算ルートとは何か？
• 塑性変形とは｜読み方・弾性変形との違い・降伏点
• 弾性変形とは？読み方・降伏点・塑性変形との境界と建築の使用限界設計
• 塑性変形能力とは？すぐに分かる意味と塑性ヒンジとの関係
• 変形増大係数とは？1分でわかる意味、木造、コンクリート、鉄骨の値
• 変形係数とは？1分でわかる意味、求め方、Ｎ値による推定、弾性係数との関係
• 剛性とは？変形しにくさの意味・強度との違い・計算式・単位を解説