1. HOME > 構造計算の基礎 > 偏心率の計算方法は？5分でわかる式、建物の重心、剛心の求め方、弾力半径、ねじり剛性の算定

偏心率の計算方法は？5分でわかる式、建物の重心、剛心の求め方、弾力半径、ねじり剛性の算定

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

偏心率とは、建物の「平面における」重さの中心（重心）とかたさの中心（剛心）のバランスを割合で表した値です。偏心率は「偏心距離÷弾力半径」で計算できます。偏心距離は重心位置と剛心位置の差、弾力半径はねじりモーメントに対する抵抗性を長さで表したものです。つまり、弾力半径が大きいほど「偏心に対して抵抗する度合いも大きくなる」ことを意味します。今回は、偏心率の計算と式、計算の考え方について説明します。偏心率、偏心距離、弾力半径の意味は下記が参考になります。

偏心率とは何か？

偏心距離ってなに？1分でわかる意味と、偏心率との関係

弾力半径とは？3分でわかる意味、定義と求め方、偏心率との関係

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

記事を書いた人

ハナダユキヒロ／建築学生が学ぶ「構造力学」

難解な構造力学、建築構造の用語を分かりやすく解説する専門家。高等専門学校在学中から建築学生が学ぶ「構造力学」を運営。その後、国立大学大学院⇒組織設計事務所⇒弊サイト運営に従事している。

著書：「わかる構造力学/工学社」、「わかる構造力学 改訂版/工学社」

LINEで質問したい方はこちら　⇒　【好評】管理人にLINEで質問してみよう

偏心率の計算方法は？式と計算の考え方

偏心率とは、建物の「平面における」重さの中心（重心）とかたさの中心（剛心）のバランスを割合で表した値です。偏心率の意味は下記も参考になります。

偏心率とは何か？

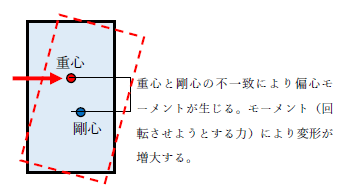
偏心率は下式で計算します。偏心距離は重心位置と剛心位置の差、弾力半径はねじりモーメントに対する抵抗性を長さで表したものです。下式は建築基準法施行令第82条の6に定義されます。

・偏心率＝偏心距離÷弾力半径

偏心率自体の計算式は簡単ですが、偏心距離と弾力半径の計算がやや面倒なので詳しく解説します。

なお、本計算（令第82条の6）による方法は、随所に、実務で使用できるように略算的な考え方を取り入れています。適用範囲（例：剛床仮定、並進架構であること、概ね整形な建物とすること等）があることに注意が必要です。

建物の重心の求め方

重心とは、重さの作用する中心です。建物の重さの中心はどのように求めるのか難しそうですが、実は考え方は簡単です。建物の問題を解く前に、まずは簡単な図形の問題を考えましょう。

さて、長方形断面の質量が一様に分布する（偏りがない）場合、長方形断面の重心は図心と一致します。

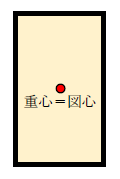
では、下図のように長方形を組み合わせた図形の重心位置はどう求めるのでしょうか。これはモーメントのつり合いを考えれば良いのです。

図心ってなに？図心の求め方と断面一次モーメントの関係

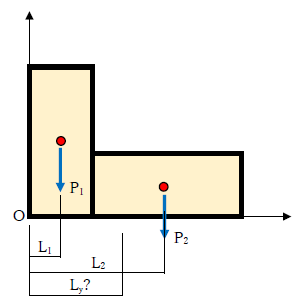
各図形に生じる力をP1、P2、図心から座標軸までの距離（X方向）をL1、L2とします。なお、前述したように各長方形断面の重心は図心と一致します。モーメントの和は、各図形の合力のモーメントと等しくなります。モーメントは「力×距離」で求めるので、

・P1×L1+ P2×L2＝（P1+ P2）×Lx

より、Lxが算定できます。Y方向の重心位置も同様に計算します。

ところで、断面一次モーメントは「ある図形の断面積×長さ（断面の図心から座標軸までの距離）の合計」で求めます。つまり、「力　⇒　断面積」と考えたモーメントが断面一次モーメントといえます。断面一次モーメント、重心位置の計算は下記もご覧ください。

断面一次モーメントについて

重心とは？1分でわかる簡単な意味、定義、求め方、公式

上記のモーメントのつり合いを用いれば、建物の平面の重心位置が算定できます。柱、壁などの鉛直部材（以下、部材）は、それぞれ長期荷重による軸力が作用しています。

軸方向力とは？1分でわかる意味、読み方、軸力との違い、求め方、圧縮軸力と引張軸力

各部材に作用する軸力をＮ、座標軸から各部材中心までの距離をＸ、Ｙとするとき、重心位置は下式で求めます。難しそうに見えるかもしれませんが、式の内容は「各モーメントの和＝合力×距離（座標軸から合力作用点までの距離）」より、合力の作用点までの距離（重心）を求めているだけのことです。なお、座標軸の原点は建物の左隅とします（どこでも良いが計算が簡単となるため）。

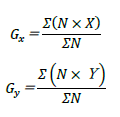
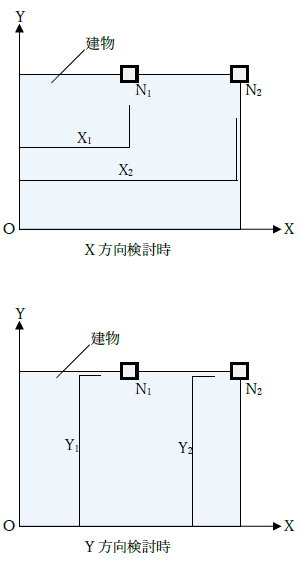
また、計算せずとも直感的に理解できますが、床荷重などが均一で建物が整形な場合は、重心位置は建物の図心位置に近くなります。

建物の重心の求め方は？3分でわかる意味、計算方法、偏心率との関係

剛心の求め方

次に剛心位置を求めます。前述と考え方は同じでモーメントのつり合いを考えます。ただし、馴染み深い「力×距離」では無くて「水平剛性×距離」という式から算定します。

なぜ、モーメントを求めるのに「剛性×距離」として良いのか理解できないと思うかもしれませんが、剛性の単位は「Ｎ/m」なので「剛性＝単位長さ当りの力」と言い換えれば、「力×距離　⇒　単位長さ当りの力×距離」に変わっても違和感は少ないでしょう。

なお、各部材の水平剛性KはD値法におけるD値を用いても良いですし、立体解析により求めた各部材のせん断力Q、せん断変形δから「K＝Q/δ」を算定しても良いです。手計算をするならD値を使います。電算（計算ソフト）では、当然、立体解析しています。

以上より、剛心は下式で算定します。

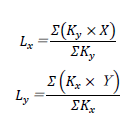
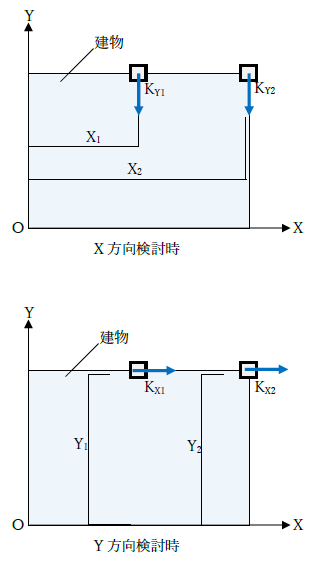
下図をみてください。KxはX方向に生じる力、KyはY方向に生じる力と考えれば、なぜ「Ky×X、Kx×Y」を計算すれば良いか分かりますね。

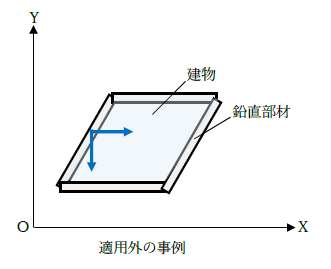
また、下図のように斜めに配置された部材がある場合、剛性はX・Y成分に分解されます。X、Y方向検討時にKxとKyの剛性（Ky×X＋Kx×Y）を考慮する必要があるため、単純に本式へ適用できません。

偏心距離の求め方

偏心距離eは、前述した「重心位置と剛心位置の引き算」です。よって、

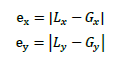
となります。ex、eyは距離なので絶対値をとります（負の距離は無い）。偏心距離の意味は下記も参考になります。

偏心距離ってなに？1分でわかる意味と、偏心率との関係

重心と剛心の距離の関係は？1分でわかる意味、偏心距離eの求め方は？

ねじり剛性の求め方

弾力半径を求める前に、ねじり剛性の算定が必要です。偏心率の計算で用いる「ねじり剛性」とは、前述した偏心モーメントによる「ねじれ」に対するかたさです。つまり、ねじり剛性が大きいほど、ねじりに抵抗できることを意味します。

下図のように地震力は重心位置に作用します。重心と剛心が一致しない場合、剛心を中心にモーメントが作用するので、建物が「ねじれる（回転する）」のです。

このような物体の回転運動に対する抵抗性は、物理学では慣性モーメントで表します。慣性モーメントは、ある物体の回転のしにくさで「質量と半径（回転半径）」が関係します。物体の質量が大きくなるほど、半径が長くなるほど、回転させにくいことが直感的に理解できるでしょう。

慣性モーメントIは下式で求めます。mは物体の質量、ｒは回転半径です。※求め方は慣性モーメントの記事をご覧ください。

また、回転させようとする力（モーメント）Ｍと慣性モーメントＩの関係は、

です。θ''は角加速度（角度θを時間tで2階微分したもの）です。上式より、慣性モーメントが大きいほど角加速度は小さくなり、すなわち「回転させにくい」ことが分かります。慣性モーメントの詳細は下記をご覧ください。

慣性モーメントとは？【近日公開予定】

断面二次極モーメントとは？1分でわかる意味、長方形の公式と計算方法、単位、断面二次モーメントとの関係

また、構造力学でいう「断面二次モーメント」は、慣性モーメントに対応する値です。質量ｍを微小断面積dＡ、rを座標軸から図心までの距離（xまたはy）とすれば、断面二次モーメントの定義式「y^2×dＡ」が得られます。

断面二次モーメントとは？1分でわかる意味、計算式、h形鋼、公式、たわみとの関係

以上より、建物の回転に対しても慣性モーメントに対応した式を立てれば、ねじり剛性（回転に対する抵抗性）が得られます。なお、部材断面のねじり剛性も同様ですが、ねじりに対する断面のかたさ（剛性）は「断面極二次モーメント」を用います。

断面二次極モーメントとは？1分でわかる意味、長方形の公式と計算方法、単位、断面二次モーメントとの関係

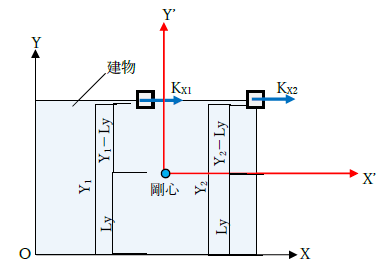
慣性モーメントの質量mを水平剛性Kx、Ky、円の方程式よりr^2は、X'^2+Y'^2に置き換えます。なお、建物（の剛心）を中とした回転のしにくさを求めたいので、座標軸は剛心位置に座標変換します。難しい話では無く、XやYの距離が変わるだけのことです。Ｘ'=X－Lx、Y'=Y－Lyです。

よって、ねじり剛性Krは下式で算定します。

上式を見ると、建物のねじり剛性は、要するに、断面極二次モーメント（＝Iy+Ix）と対応することが分かりますね。

弾力半径の求め方

弾力半径は、建物のねじりに対する抵抗の度合いを距離で表したものです。弾力半径は、構造力学で習う「断面二次半径」に対応します。

前述したように、回転運動は「質量ｍと回転半径ｒが大きいほど回転しにくい」と言えます。これは直感的に理解できます。半径の大きな滑車（車輪）と、小さな滑車でどちらが回しやすいかイメージしてみましょう。

以上より、弾力半径が大きいほど「ねじりに抵抗できる」のです。回転半径rは下式で求められます。

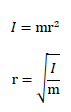
ねじり剛性Krは慣性モーメントIを元に算定しました。よって、IとKr、回転半径rと弾力半径re、質量ｍと水平剛性Ｋは対応関係にあります。以上より、弾力半径は、

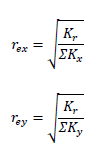
で求められます。上式は、断面二次モーメントIと断面二次半径i、断面積Aの関係に対応します。つまり、断面二次半径が大きいほど曲げモーメントに対する抵抗性が高いと言えるのです。

弾力半径とは？3分でわかる意味、定義と求め方、偏心率との関係

断面二次半径とは？1分でわかる意味、公式、計算、座屈、断面二次モーメントとの関係

偏心率の算定

前述したように偏心率は、偏心距離÷弾力半径で算定します。よって、

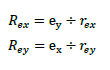
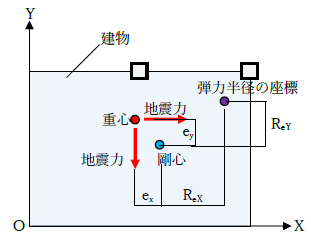
です。なお、下図のようにX方向加力時にはY方向の偏心距離eyがねじれやすさを表し、rexがねじれ抵抗の度合いです。Y方向加力時には偏心距離exがねじれやすさで、reyがねじれ抵抗の度合いを意味します。

以上のように偏心率の計算は、

・モーメントのつり合い

を基本的な考え方として求めます。途中、慣性モーメントの考え方が必要になりますが、全体を通して、そこまで難しくない内容だと思います。

実際の構造設計では、上記で解説した偏心率を「一貫計算プログラム」により求めます。手計算することなく勝手に出てくる値です。

よって、計算式の内容を理解して、適用範囲および「どうすれば偏心率を下げられるのか」なども勉強しましょう。

偏心率を下げる方法は？偏心距離、弾力半径との関係

まとめ

今回は、偏心率の計算について説明しました。建物の偏心率は「偏心距離÷弾力半径」で計算します。この計算式自体は簡単ですが、偏心距離や弾力半径の算定には「モーメントのつり合い」や「慣性モーメント」の考え方が求められます。下記も併せて参考にしてくださいね。

偏心率とは何か？

慣性モーメントとは？【近日公開予定】

台形の重心は？1分でわかる意味、重心位置の求め方、面積

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

▼スポンサーリンク▼

【初回資料が今だけ無料！】1日約13円で情報をアップデート！

有料メルマガを無料で見てみませんか？⇒　忙しい社会人、学生のためのビルディング・アップデート

更新情報

• 当サイトでは、ほぼ毎日、記事更新・追加を行っております。


• 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。


• 新着記事一覧

プロフィール

• 
• 略歴▼
• 名前　ハナダユキヒロ/MITUME lab代表.
• 2010年　弊サイトを開設
• 2010～2017年　国立大学大学院修了
• 2017年12月に当HPが書籍化。
• 「わかる構造力学」
• 2022年4月に「わかる構造力学」の改訂版出版。
• 「わかる構造力学(改訂版)」


• 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。


• 当サイトの目的▼
• 建築学生が学ぶ「構造力学」の目的


• とりあえず10記事▼
• 初めましての方に10記事用意しました


• おすすめ書籍紹介▼
• ハナダユキヒロが建築関連書籍の良書を選びました

建築の本、紹介します。▼

▼【好評！】管理人おすすめ▼

• あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！

同じカテゴリの記事一覧

• 偏心とは？1分でわかる意味、偏芯との違い、偏心率の目安、偏心量、偏心距離1/6との関係
• 偏心率とは何か？
• 偏心率を下げる方法は？偏心距離、弾力半径との関係
• 偏心距離ってなに？1分でわかる意味と、偏心率との関係
• 重心とは？1分でわかる簡単な意味、定義、求め方、公式
• 建物の重心の求め方は？3分でわかる意味、計算方法、偏心率との関係
• 重心と剛心の距離の関係は？1分でわかる意味、偏心距離eの求め方は？
• 弾力半径とは？3分でわかる意味、定義と求め方、偏心率との関係
• 保有水平耐力とは何か？
• 必要保有水平耐力の算定方法と意味がわかる、たった３つのポイント