【好評】LINEで質問構造力学が苦手おすすめ書籍おすすめPDF教材無料メルマガ図解集用語集

HOME > 材料力学の基礎 > 応力集中と応力集中係数の基礎知識

応力集中と応力集中係数の基礎知識

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

応力集中とは、応力がある部分に集中することです。

応力集中は、部材が不連続になる箇所等で生じます。たとえば、鋼材の接合部に高力ボルトを留めるため孔を空けた周辺等が該当します。

応力集中や、応力集中の度合いを示す応力集中係数は、接合部周りの応力度の大きさを知る上で役に立ちます。

今回は、応力集中係数の意味や求め方、応力集中の意味について説明します。

※応力、応力度については、下記が参考になります。

応力とは？1分でわかる意味と種類、記号、計算法

応力度の基礎知識、応力度の種類と1分でわかる応力との違い

応力集中とは？

例えば、切り欠きのある鋼材を引張ると応力は均一ではなく、切り欠き周辺に集中します。また、円孔が空く鋼材も同様に、円孔周りに応力が集中します。

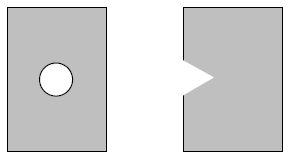
円孔の空いた鋼材

このように、応力が均一ではなくある部分に集中することを「応力集中」と言います。

また、建築分野では「鋼材の切り欠き、円孔」のようなミクロな視点の応力集中もあれば、柱や梁などのマクロな視点での応力集中も話題にします。これは後述します。

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

記事を書いた人

ハナダユキヒロ／建築学生が学ぶ「構造力学」

難解な構造力学、建築構造の用語を分かりやすく解説する専門家。高等専門学校在学中から建築学生が学ぶ「構造力学」を運営。その後、国立大学大学院⇒組織設計事務所⇒弊サイト運営に従事している。

著書：「わかる構造力学/工学社」、「わかる構造力学改訂版/工学社」

LINEで質問したい方はこちら　⇒　【好評】管理人にLINEで質問してみよう

応力集中係数の意味と計算方法

応力集中係数とは、下式で計算します。

応力集中係数α＝最大応力(σmax)／平均応力(σ)

ただ問題は、「最大応力をどのように計算するのか」ということです。

今回は円孔のあく平板に引張力が作用するときの、最大応力の計算方法と、応力集中係数を求めます。※引張力については、下記が参考になります。

引張、圧縮とは？1分でわかる意味、違い、符号、強度の関係

下式をみてください。これは、円孔の空く平板の応力度を求める式です。σは応力度、aは円孔の半径、yは縦軸の未知数、σxはx軸の未知数（つまり応力度）です。

⁴

下記で示すように、上式はσxを求める関数です。yに数値を代入すれば、その位置での応力が分かります。円孔近傍の応力を知りたいので、半径aをyに代入します。

y=aのとき

σx＝σ（1+( a²／2a²) +(3a⁴／2a⁴)）

　＝σ（1+1／2+3／2）＝3σ

です。このとき「3」を応力集中係数といいます。yを大きくするに従って、「3」は「1」に近づきます（平均応力度に近づく）。

接合部の応力集中を、構造力学の視点から考える

接合部の応力集中を、構造力学の視点から考えます。同様に円孔の空く平板を例にしましょう。構造力学では、力が流れるか否かを考えます。

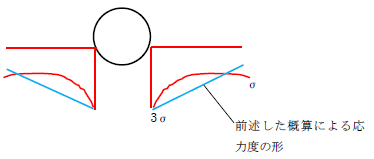
引張力が作用するとき、円孔が空いている部分は応力が流れません（当たり前ですが、中空なので力は伝達しない）。下図をみてください。

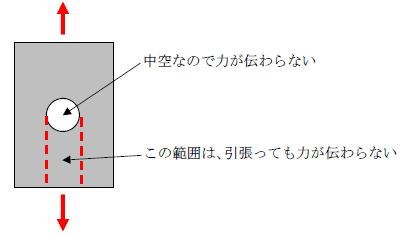
力の伝達メカニズム

つまり力が伝達しない円孔の応力は、別の箇所に流れる必要があります。

このとき力の流れは「最も近い位置に流れる」のが普通です。つまり、円孔の近傍に伝達しない応力が作用します。

元々の応力度がσとするなら、円孔周りにはσ'（σより大きい値）が作用します。

円孔に作用する荷重は、どのように伝達されるのでしょうか。仮に、円孔近傍を固定支点と考えると、片持ち形状とみえます。

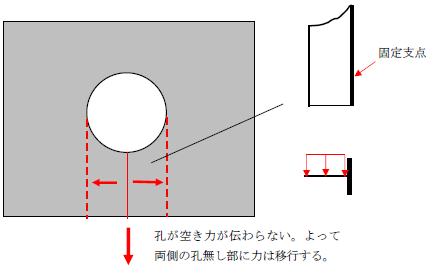
円孔の空く鋼板を構造力学的にモデル化

片持ち梁には曲げ応力度が作用します。曲げ応力度は圧縮と引張側に応力度が作用します。

元々は引張側にのみ応力度が発生しているので、２つを合算すると下図の応力度図になります（もちろん正しくはありません）。

※片持ち梁、曲げ応力度については、下記が参考になります。

片持ち梁とは？1分でわかる構造、様々な荷重による応力と例題

曲げ応力とは？1分でわかる意味、公式と演習問題、単位、曲げ応力度との違い

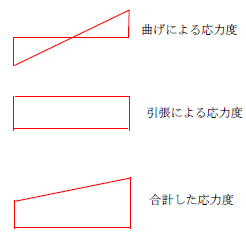
鋼板の応力度

つまり、難しい数式を知らなくても「どこに応力が集中するのか？」大体の見当は付くのです（実際の円孔周りの応力度は下図となる）。

円孔周りの応力

耐震要素の応力集中と、接合部の応力集中

前述した円孔や切り欠きの話題は、実は建築であまり問題にしません。細かい部品を厚保かう機械工学の分野です。建築では巨視的な視点の、応力集中を問題にします。

下図をみてください。これは平面的に耐震要素を示しました。左側のみ耐震壁があり、あとは柱と梁だけです。

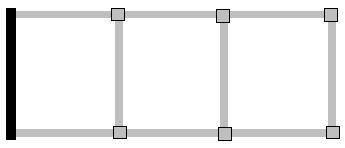
部材の応力集中

地震力が作用するとき、どこに応力が集中するでしょうか？答えは「耐震壁」です。

剛性の大きな部材に力が集まる原則を知っていれば、ごく当たり前のことです。

建築を勉強するなら、前述した応力集中や応力集中係数よりも、耐震要素のどこに応力が集まるのか、理解した方が良いでしょう。

剛性、剛比については、下記が参考になります。

剛性ってなに？剛性の算定と、軸方向応力、ポアソン比、ひずみの関係

剛比とは？3分でわかる剛比の意味と計算方法

地震力、耐震壁については、下記が参考になります。

地震力の算定方法と、簡単にわかるZ、Rt、Ai、Coの意味

耐震壁ってなに？すぐに分かる耐震壁の意味と役割、耐力壁との違い

まとめ

今回は応力集中と応力集中係数について説明しました。応力集中係数の計算方法も大事ですが、

「どこに応力が集中するのか」把握する考え方を身に付けましょう。下記も併せて学習しましょう。

応力とは？1分でわかる意味と種類、記号、計算法

応力度の基礎知識、応力度の種類と1分でわかる応力との違い

繰り返し応力とは？1分でわかる意味、s-n曲線、疲労限、応力集中との関係

▼スポンサーリンク▼

▼【好評！】管理人おすすめ▼

あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！

▼用語の意味知らなくて大丈夫？▼

▼同じカテゴリの記事一覧▼

▼カテゴリ一覧▼

▼他の勉強がしたい方はこちら▼

noteで学ぶ建築士試験の構造

ゼロから建築士試験の構造を勉強しよう～！

ゼロから学ぶ建築士試験の構造

【好評】LINEで質問！

管理人に質問してみる？

わかる1級建築士の計算問題解説書

【初回資料が今だけ無料！】1日約13円で情報をアップデート！

有料メルマガを無料で見てみませんか？⇒　忙しい社会人、学生のためのビルディング・アップデート

わかる2級建築士の計算問題解説書！

【30%OFF】一級建築士対策も◎！構造がわかるお得な用語集

更新情報

当サイトでは、ほぼ毎日、記事更新・追加を行っております。

更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。

新着記事一覧

プロフィール

略歴▼
名前　ハナダユキヒロ/MITUME lab代表.
2010年　弊サイトを開設
2010～2017年　国立大学大学院修了
2017年12月に当HPが書籍化。
「わかる構造力学」
2022年4月に「わかる構造力学」の改訂版出版。
「わかる構造力学(改訂版)」

10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。

当サイトの目的▼
建築学生が学ぶ「構造力学」の目的

とりあえず10記事▼
初めましての方に10記事用意しました

おすすめ書籍紹介▼
ハナダユキヒロが建築関連書籍の良書を選びました

建築の本、紹介します。▼

▼【好評！】管理人おすすめ▼

あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！

同じカテゴリの記事一覧

Topへ >>