1. HOME > 構造計算の基礎 > 地震力の算定方法と、簡単にわかるZ、Rt、Ai、Coの意味

地震力の算定方法と、簡単にわかるZ、Rt、Ai、Coの意味

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

構造物に作用する外力は大まかに分けて２つあることを、『長期荷重と短期荷重』の記事で説明しました。長期荷重と短期荷重の違いは下記が参考になります。

長期荷重・短期荷重

短期荷重の１つが、皆さんも良く知っている『地震力』です。では、この地震力はどのように算定するのでしょうか。また建物にどう作用するのでしょうか？

今回は地震力の算定方法、地震力の作用位置、地震力の算定に欠かせないキーワード「Z、Rt、Ai、Co」の意味について説明します。

地震の大きさには、中地震と大地震があります。下記も参考になります。

中地震とは？1分でわかる意味、震度との関係、大地震との違い

極めて稀とは？1分でわかる意味、稀との違い、地震力の大きさ、震度

地震力はどこに作用するのか？

「建築物の耐震設計」と聞くと、とても高度な計算を行っているように思います。しかし、実際は建物や地震力を単純化（モデル化）しています。

本来地震力は建物全体に作用しますが、それでは計算が複雑過ぎるからです。

※但し、特殊な建物（スカイツリー）や超高層ビルは、実際の揺れ方などを解析します。「振動解析」といいます。

多質点系の時刻歴応答解析

そこで、建築物に作用する地震力は「床」に、「集中荷重として」作用すると考えます。なぜ床に作用すると考えるのか。

それは、地震力のような水平方向の力に対して柱や梁は断面積が小さく、一方床は大きな断面積です。つまり、床の剛性はとても大きいのです。

剛性が大きな部材に力が集まる、という構造力学の原則に基づけば「地震力は床に作用する」という考えは必然ですね。この考え方を「剛床仮定」といいます。

さて、前述した地震力を私達は専門用語で『層せん断力』とも言います。「地震力＝層せん断力」ということです。

では次に、地震力の算定方法について勉強しましょう。

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

記事を書いた人

ハナダユキヒロ／建築学生が学ぶ「構造力学」

難解な構造力学、建築構造の用語を分かりやすく解説する専門家。高等専門学校在学中から建築学生が学ぶ「構造力学」を運営。その後、国立大学大学院⇒組織設計事務所⇒弊サイト運営に従事している。

著書：「わかる構造力学/工学社」、「わかる構造力学 改訂版/工学社」

LINEで質問したい方はこちら　⇒　【好評】管理人にLINEで質問してみよう

地震力の算定方法

地震力は下式で算定できます。

Q=W×Ci

Qは地震力、Wは地震用重量（つまり建物の重さ）、Ciは層せん断力係数です。さらに層せん断力係数Ciは下式で算定されます。

Ci＝Z×Rt×Ai×Co

Zは過去の地震記録に基づく国土交通省が定める値です。地震の起きやすさを数値化した値と考えてください。

Rtは振動特性係数、Aiは地震層せん断力係数の高さ方向の分布、Coを標準せん断力係数といいます。

それぞれの用語について説明します。最終的に地震力の算定方法を理解しましょう。※層せん断力係数については、下記が参考になります。

地震層せん断力係数とは？1分でわかる意味、上層、ベースシア係数、地震力との関係

標準せん断力係数Coの算定方法と意味

地震力は、地面が揺れることで建物が振られ、その際に発生する慣性力です。

地震力は建物重量が大きく関係し、例えば軽い構造物だと地震力が小さく、重い建物ほど地震力は大きくなります（前述した地震力の式をご覧ください）。

過去、日本内外で発生した地震を取りまとめ、先人達が様々な分析を行った結果、現在の法律では、

地震力＝建物の重量×0.2（もしくは0.3）

とされています。この0.2や0.3の係数をベースシェアー（標準せん断力係数）Coと呼んでいます。

建築基準法では、Co＝0.2のベースシェア―で中程度の地震（この地震力を外力とした設計を１次設計と呼ぶ）、大地震時でCo＝1.0のベースシェア―（２次設計時の外力）と考えています。

また靭性を期待しない建物（強度は高いが変形しない建物）は、Co＝0.3のベースシェアーとします。

0.2と0.3の使い分けは、「構造計算ルート」が関わっています。下記が参考になります。

構造計算ルートとは何か？

さて、Coを整理すると下記となります。

• 中程度の地震　Co=0.2（または0.3）
• 大規模の地震　Co=1.0

このベースシェアーが意味することは、建物重量に対して「2割、3割が地震の力になる」ということです。実はCoの値は下記のように、別の見方もできます。

• Co＝0.2　⇒　200gal（gal＝0.001cm/s^2）
• Co＝1.0　⇒　1000gal（gal＝0.001cm/s^2）

ピンときた方もいるかもしれませんが、1000galとは1ｇすなわち重力加速度と同じ値なのです。

つまり建築基準法では、大地震時に想定する地震力を「建物の重量と同じ値で考える」としています。

中程度の地震、大規模の地震の詳細は下記が参考になります。

中地震とは？1分でわかる意味、震度との関係、大地震との違い

極めて稀とは？1分でわかる意味、稀との違い、地震力の大きさ、震度

回りくどいかもしれませんが、もう１つ別の考え方をすれば、大地震時は「建物を真横に倒しても大丈夫か」というレベルの検討をするわけです。

地震用重量Wとは何か？

地震力の算定式は下記です。

Q=W×Ci

では、簡単に書きましたが「建物の重量W」とは、どういうことでしょう？どうやって算定するのでしょうか。

仮に3層の建物を想定すると、建物重量はどう振り分けて、各層の床にせん断力として作用させるべきでしょう。

これは、力の伝わり方によって様々な議論があるわけですが、基本的な考え方として『階高の1/2の重量を地震用重量』としています。

上図のように重量は振り分けるわけです。

Zの算定方法と意味

次にZの算定方法と意味について説明します。Zとは層せん断力係数Ciを算定するとき必要な係数でしたね。

Zは、各地方における過去の地震記録に基づく地震被害の程度、地震活動の状況に応じて国土交通大臣が定める値です。

Zは1.0～0.7の範囲内で定められています。ざっくり言えば、「地震が多い地域は1.0、地震が少ない地域は0.7」と覚えておけば大丈夫です。

沖縄は地震が少ないため、Z=0.7に設定されます。他にも島根県や岡山県、広島県などの中国地方、北海道はZ＝0.9など地震力を低減できるよう値が設定されています。

各都道府県の市町村郡によって定められています。HPで公開されているので、気になる地域の値を確認してみましょう。地震地域係数の詳細は、下記が参考になります。

地震地域係数とは？1分でわかる意味、一覧、沖縄、東京都、名古屋

振動特性係数Rｔの算定方法と意味

振動特性係数Rtは、建物の固有周期及び地盤の種別に応じて、地震力の値を変化させる係数です。Rtは下表の式により算定します。

また、Tcは下表から選びます。

Tcの値は地盤の区分により変化します。これは感覚的に掴んでほしいのですが、第１種地盤は「良い地盤」。

固くて直接基礎にできそうな地盤」のことです。一方、第３種地盤は沖積層と言い、いわゆる「軟弱地盤」です。

液状化するような地盤は第３種地盤に該当します。第２種地盤は、それ以外の地盤です。

また固有周期Tは下式から算定できます。

T=ｈ（0.02+0.01α）

Tは固有周期、ｈは建物の高さ、αは建物の高さに対して、鉄骨造である階の高さの合計のｈに対する比です。

αについて少し説明します。固有周期の詳細は下記が参考になります。

固有周期の基礎知識と、3分でわかる計算方法

例えばRC造の建物があります。αは鉄骨造である階の高さの合計のｈに対する比ですから、α＝0です。

また、全階が鉄骨造ならα＝1.0です。例えば３階建てで、３階部分のみ鉄骨造の場合、これは「３階の階高／建物高さ」がαとなります。

さて、Rtの算定方法は前述した通りですが、意味を考えてみます。Rtの算定は３つの条件下で計算式が違いました。最も簡単な下式をみると、

T＜Tcの場合　Rt=1.0

でしたね。Tは建物の固有周期で、Tcと比較しています。つまりTcは地盤の固有周期です。

T＜TcでRt＝0とは「地盤の周期より建物の周期が短いなら、建物は普通に揺れるよ」という意味です。

2Tc≦Tの場合　Rt=1.6Tc／T

の状況では、地盤の固有周期より建物の固有周期が大分長いですね。このとき、Rtは1.0以下の値であり、地震力は小さくなります。

Ai分布の算定方法と意味

最後にAiについて勉強します。Aiとは高さ方向の層せん断力係数の分布です。

前述した標準せん断力係数Coは、あくまでも１層目の値を示したに過ぎません。

建物の中には、１０階、２０階、最近ではもっと高い超高層ビルさえあります。

それらの建物に作用する地震力（層せん断力係数の分布）は、１層と同じ力で分布するとは思えませんね。上に行くほど大きくなる？あるいは小さいことも考えられます。

本来、地震力の分布は振動解析を行い求めるのですが、建築基準法では振動解析という高度な計算を行わずとも算定できる方法があります。

それが「Ai分布」です。要するに、地震力の高さ方向の分布を便宜的に決めた値です。Ai分布は下式より算定されます。

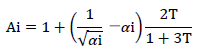
Tは建物の固有周期で、前述した算定式で求めます。

αiはAiを算出しようとする高さの部分が支える部分の固定荷重と積載荷重との和を、建築物の地上部分の固定荷重と積載荷重との和で除した値、と定義されます。

つまりAiを算出したい層の重量を、全重量で除すことで算定できます。

上記に示したAi分布を計算すると、最上階が最も大きいせん断力係数の値となり、徐々に標準せん断力係数の値になります。

地下部分の地震力の算定方法

地下の地震力の算定は、とても簡単です。

ｋ≧0.1（1－H／40）×Z

ｋは水平震度（地上のCoとほぼ同義）、Hは地下部分の地面からの高さ、Zは前述した値です。

ただ、建築設計の実務では、40ｍの地下建物はほとんど考えられないので、ｋ＝0.1として差し支えないでしょう。

ｋ＝0.1である理由ですが、地下は、土がクッション材として働く分、地上より地震力が小さいのです。

まとめ

以上、地震力の算定方法について勉強しました。地震力の算定式自体は

Q=W×Ci

なので簡単です。但し、下式のように層せん断力係数の算定に用いられる係数が難解です。

Ci＝Z×Rt×Ai×Co

今回、各係数の算定方法や意味について詳細に説明しました。ぜひ、地震力の算定に活かして頂ければと思います。下記も併せて参考にしてください。

地震層せん断力係数とは？1分でわかる意味、上層、ベースシア係数、地震力との関係

ベースシア係数とは？1分でわかる意味、計算方法、層せん断力係数との関係

地震地域係数とは？1分でわかる意味、一覧、沖縄、東京都、名古屋

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

▼スポンサーリンク▼

【初回資料が今だけ無料！】1日約13円で情報をアップデート！

有料メルマガを無料で見てみませんか？⇒　忙しい社会人、学生のためのビルディング・アップデート

更新情報

• 当サイトでは、ほぼ毎日、記事更新・追加を行っております。


• 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。


• 新着記事一覧

プロフィール

• 
• 略歴▼
• 名前　ハナダユキヒロ/MITUME lab代表.
• 2010年　弊サイトを開設
• 2010～2017年　国立大学大学院修了
• 2017年12月に当HPが書籍化。
• 「わかる構造力学」
• 2022年4月に「わかる構造力学」の改訂版出版。
• 「わかる構造力学(改訂版)」


• 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。


• 当サイトの目的▼
• 建築学生が学ぶ「構造力学」の目的


• とりあえず10記事▼
• 初めましての方に10記事用意しました


• おすすめ書籍紹介▼
• ハナダユキヒロが建築関連書籍の良書を選びました

建築の本、紹介します。▼

▼【好評！】管理人おすすめ▼

• あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！

同じカテゴリの記事一覧

• 地震層せん断力係数とは？1分でわかる意味、上層、ベースシア係数、地震力との関係
• ベースシア係数とは？1分でわかる意味、計算方法、層せん断力係数との関係
• 地震地域係数とは？1分でわかる意味、一覧、沖縄、東京都、名古屋、静岡の値
• 中地震とは？1分でわかる意味、震度との関係、大地震との違い
• 極めて稀とは？1分でわかる意味、稀との違い、地震力の大きさ、震度との関係
• 耐震設計とは？1分でわかる意味、考え方、震度との関係、制震、免震との違い
• 重要度係数がよくわかる、重要度係数と耐震性能の関係について
• 共振とは？1分でわかる意味、原理、地震、固有周期との関係
• 突出部の水平震度は？1分でわかる意味、地震力の求め方、突出部の例
• 震度階とは？1分でわかる意味、計測震度、段階、加速度、galとの関係
• 必要保有水平耐力の算定方法と意味がわかる、たった3つのポイント
• 一次設計とは？1分でわかる意味、震度との関係、二次設計との違い
• 二次設計とは？1分でわかる意味、目的、保有水平耐力計算