1. HOME > 鉄筋コンクリート造の基礎 > ゲルバー梁とは？1分でわかる意味、解き方、利点と単純梁との違い、応力、静定構造物との関係

ゲルバー梁とは？1分でわかる意味、解き方、利点と単純梁との違い、応力、静定構造物との関係

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

ゲルバー梁とは、連続梁にヒンジ（ピン接合部）を設け静定構造にした梁です。単純梁に比べて、応力やたわみを小さくすることが可能です。今回はゲルバー梁の意味、解き方、利点単純梁との違い、応力、静定構造物との関係について説明します。梁の反力、応力の求め方は、下記が参考になります。

梁の反力と、演習問題から学ぶ計算方法

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

記事を書いた人

ハナダユキヒロ／建築学生が学ぶ「構造力学」

難解な構造力学、建築構造の用語を分かりやすく解説する専門家。高等専門学校在学中から建築学生が学ぶ「構造力学」を運営。その後、国立大学大学院⇒組織設計事務所⇒弊サイト運営に従事している。

著書：「わかる構造力学/工学社」、「わかる構造力学 改訂版/工学社」

LINEで質問したい方はこちら　⇒　【好評】管理人にLINEで質問してみよう

ゲルバー梁とは？

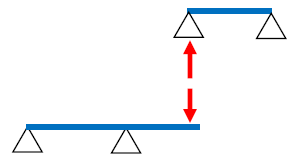
ゲルバー梁とは、連続梁にヒンジ（ピン接合部）を設け、静定構造にした梁です。下図をみてください。これがゲルバー梁です。

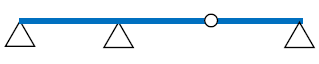
ヒンジとは、ピン接合部のことです。鉛直、水平方向を拘束しますが、回転方向は自由に変形できます。よって、曲げモーメントが0になります。ピン接合の意味は、下記が参考になります。

剛接合とピン接合の意味と、納まりと構造性能の違い

普通、連続梁は不静定構造です。不静定構造は、力のつり合い条件だけでは解けず、やや複雑な計算を要します。

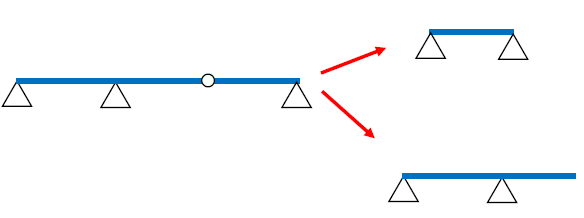
一方、ゲルバー梁は「ヒンジを設けること」で不静定次数を減らすことが可能です。例えば、上図の例では反力数が4つですが、ヒンジが１つあるため「4－1＝3」の反力数と考えて良いです。つまり静定構造です。

なぜ反力数を１つ減らすことができるのでしょうか。下図をみてください。ゲルバー梁の「ヒンジ」は、ピン接合です。ヒンジを境に、２つの静定構造に分解しましょう。分解した２つの梁は静定構造です。２つの梁を重ね合わせれば元のゲルバー梁になります。

ゲルバー梁の解き方

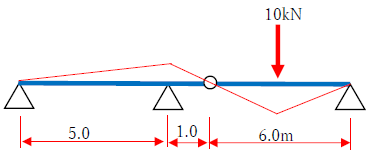
ゲルバー梁を解きましょう。下図をみてください。2スパンの連続梁です。ヒンジがあるので、ゲルバー梁です。

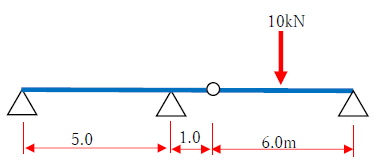
ゲルバー梁は、ヒンジを境に複数の静定梁に分解できました。下図に示します。

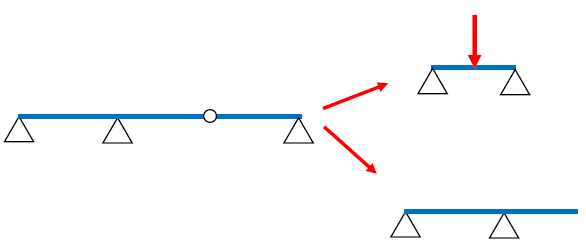
分解した静定梁を個別に解いて、応力またはたわみを重ね合わせれば最終的な結果となります。

まず分解した単純梁の反力は、

R=10÷2＝5kN

です。最大曲げモーメントは、

M=5×3＝15kNm

です。

ここで注意したいのが、単純梁の右側支点の反力は、もう一方の静定梁に「荷重として作用する」ことです。下図をみてください。分解した梁の支点が、張出部分に「載っている」ので、その重さは張出部分に作用しますよね。

さて、もう一方の静定梁を解きます。荷重は張出部分に作用しますよって、

P=5ｋN

R=5×1÷6＝5/6

です。上記の反力Rが、２つの支点に正反力、負反力として作用します。曲げモーメントは、片持ち曲げの計算と同様に、

M=5×1＝5kNm

です。以上を重ね合わせると、ゲルバー梁の曲げモーメント図は下記です。

梁の解き方、反力の求め方は下記の記事が参考になります。

梁の反力と、演習問題から学ぶ計算方法

ゲルバー梁の利点と応力、単純梁（静定構造物）との違い

ゲルバー梁の利点を下記に示します。

不静定梁に比べて計算が簡単

単純梁に比べて、応力を減らすことが可能

単純梁に比べて、たわみを減らすことが可能

ゲルバー梁は静定構造なので、不静定梁に比べて計算が簡単です。また、梁の諸条件によりますが、ゲルバー梁は応力やたわみを減らすことができます。単純梁の意味は、下記が参考になります。

梁の種類とは？1分でわかる種類と構造

下図をみてください。単純梁の中央に荷重が作用します。中央に最大曲げモーメントとたわみが生じます。

次に、上図の単純梁にもう１つ支点を設けて、中央の支点左側にヒンジを設けます。前述より、ゲルバー梁は複数の静定梁に分解できます。分解後の静定梁を見てください。元よりスパンの短い単純梁と、張出梁があります。

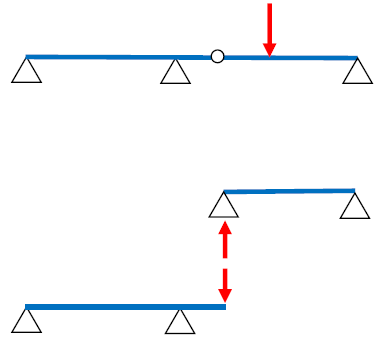
スパンが短くなる分、応力とたわみは減ります。張出梁の片持ち長さが短ければ（意図的に短くする）、片持ちの応力も僅かです。

ゲルバー梁はヒンジを境に分解すると、張出部分がでてきます。スパン中央で最大だった曲げモーメントが、張出部分の負曲げに引張られて減ったと考えることも可能です。同じことが、たわみにも言えます。

まとめ

今回はゲルバー梁について説明しました。意味が理解頂けたと思います。ゲルバー梁は、連続梁にヒンジを設けたものです。不静定梁である連続梁に比べて、簡単に反力や応力が計算できます。ゲルバー梁の利点、応力とたわみの関係を覚えましょう。解き方の基本も理解しましょうね。梁の解き方は、下記も参考になります。

梁の反力と、演習問題から学ぶ計算方法

【管理人おすすめ！】セットで3割もお得！大好評の用語集と図解集のセット⇒　建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！）

▼スポンサーリンク▼

【初回資料が今だけ無料！】1日約13円で情報をアップデート！

有料メルマガを無料で見てみませんか？⇒　忙しい社会人、学生のためのビルディング・アップデート

更新情報

• 当サイトでは、ほぼ毎日、記事更新・追加を行っております。


• 更新情報として、先月分の新着記事を一覧表示しております。下記をご確認ください。


• 新着記事一覧

プロフィール

• 
• 略歴▼
• 名前　ハナダユキヒロ/MITUME lab代表.
• 2010年　弊サイトを開設
• 2010～2017年　国立大学大学院修了
• 2017年12月に当HPが書籍化。
• 「わかる構造力学」
• 2022年4月に「わかる構造力学」の改訂版出版。
• 「わかる構造力学(改訂版)」


• 10数年以上、建築の学問、研究、構造設計の実務に携わった経験を元に、未経験の方、建築関係の学生、社会人の方に役立つ知識を、分かりやすくお伝えします。


• 当サイトの目的▼
• 建築学生が学ぶ「構造力学」の目的


• とりあえず10記事▼
• 初めましての方に10記事用意しました


• おすすめ書籍紹介▼
• ハナダユキヒロが建築関連書籍の良書を選びました

建築の本、紹介します。▼

▼【好評！】管理人おすすめ▼

• あなたも管理人に直接質問してみませんか？→【好評】LINEで質問！

同じカテゴリの記事一覧

• スランプ試験ってなに？スランプコーンとスランプ値、Fcとの関係
• 設計基準強度と品質基準強度の違いと、５分で分かるそれぞれの意味
• スラブってなに？現役設計者が教えるスラブの意味と、特徴、役割
• 増打ちってなに？増打ちの意味と納まり詳細図の描き方
• パラペットの特徴や設ける理由がすぐにわかる、たった１つのポイント
• ハンチってなに？現役設計者が教えるハンチの目的と種類
• JASS5ってなに？１分で分かるJASS5の意味について
• 骨材に必要な性質と、粗骨材と細骨材の違いがわかるたった１つのポイント
• セメントとモルタル、コンクリートの特徴、違いを知るたった１つのポイント
• コンクリートの比重は？鉄筋コンクリートとの違い、骨材、鉄筋の影響
• コンクリートの種類は？よくわかる７種類のコンクリートの特徴
• 普通コンクリートってなに？普通コンクリートの特徴、空気量、セメント量の規格
• 軽量コンクリートの特徴と使用箇所について
• 高流動コンクリートと高性能ＡＥ減水材とは何か？
• 生コンとモルタルの比重の違いは？砕石と砂の比重との関係
• PC構造と理論
• 耐震スリットってなに？耐震スリットの意味と目的、構造スリットとの違い
• スリーブってなに？梁のスリーブ位置や間隔、孔径、スリーブ補強
• フラットスラブってなに？フラットスラブのメリットとデメリット
• 開口周比ってなに？1分で分かる開口周比の意味と計算方法
• あと施工アンカーってなに？1分でわかる種類と使い方
• 接着系アンカーってなに？1分でわかる意味と材質、埋込長さ
• 金属系アンカーってなに？1分でわかる意味と材質、埋込長さ