構造図解で一発理解建築用語サクッと理解構造力学が苦手おすすめ書籍おすすめPDF教材 noteで学ぶ

HOME > 鉄筋コンクリート造の基礎 > ねじりとは？1分でわかる意味、応力、ねじり剛性、計算方法、丸棒との関係

ねじり意味応力ねじり剛性計算丸棒建築部材

この記事の要点

ねじりは部材が回転するように変形する現象です。

ねじりモーメント・ねじり応力の計算とねじり剛性の意味、丸棒と断面形状の関係を解説します。

ねじりに対する抵抗の大きさをねじり剛性（GJ）といい、せん断弾性係数Gとねじり定数Jの積で表される。

断面形状によってJの値が大きく変わる点が重要。

【管理人おすすめ！】セットで3割もお得！約1,100語の用語集＋476点の図解集セット⇒　建築構造がわかる基礎用語集＆図解集セット

ねじりとは、雑巾を絞ったような状態になる作用です。

ねじりを起こすモーメントを、ねじりモーメントといいます。

構造部材は、なるべく「ねじり」が起きないよう設計します。

今回はねじりの意味、応力、ねじり剛性との関係、丸棒のねじりの計算方法について説明します。

ねじりモーメント、ねじり剛性の意味は、下記が参考になります。

ねじりモーメントとは？1分でわかる意味、公式、単位、トルクとの関係、h鋼

ねじり剛性とは？意味・計算方法・単位と剛性との違いを解説

100円から読める！ネット不要！印刷しても読みやすいPDF記事はこちら⇒　いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のPDF版の学習記事

ねじりとは？

ねじりとは、雑巾を絞ったような状態になる作用です。下図をみてください。ねじりを加えた棒は、このように変形します。

ねじり

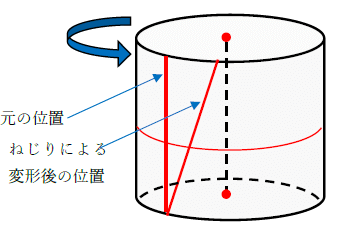
※試しに雑巾や布をねじってみましょう。

また、ねじりを起こすモーメントを、ねじりモーメントといいます。構造部材には、ねじりモーメントが起きないよう設計します。ねじりモーメントの意味、鉄骨部材との関係など、下記が参考になります。

ねじりモーメントとは？1分でわかる意味、公式、単位、トルクとの関係、h鋼

鉄骨梁のねじり検討とは？ねじり定数・ねじり応力度の計算方法

丸棒のねじりと計算方法、応力とねじり剛性の関係

ねじりによる応力、ねじり剛性を計算する場合、よく丸棒の例を使います。下図をみてください。下端を固定した丸棒があります。丸棒にねじりモーメントTを作用させると、下図のように変形します。

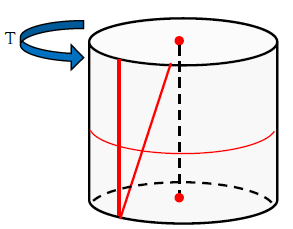
丸棒のねじり

元の鉛直線がねじりにより、斜めの線になりましたね。ただし、固定端の点は変わりません。固定されており変形しようが無いからです。今回、丸棒の１つの線に着目しましたが、当然、ねじりの作用は「円周上」で起きています。

さて、見方を変えて、ねじられた丸棒を真正面から見ます。下図をみてください。これは、せん断変形と同じだと思いませんか。

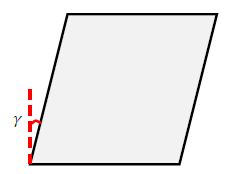
ねじりによる変形とせん断変形

せん断変形の意味は下記が参考になります。

材料力学の基礎-せん断ひずみ（yahoo知恵袋の件）-

部材が変形するとき、応力も生じています。例えば、棒が伸びる時、部材には引張力が生じています。せん断変形が起きる時、せん断応力が生じます。「ねじり」による変形は、せん断変形でした。これと対応する応力は「せん断応力」です。

つまり、ねじりが作用するとき、「せん断応力」が生じるのです。せん断応力は下式で計算します。

τ＝Gγ

τはせん断応力、Gはせん断弾性係数、γはせん断ひずみです。せん断応力の意味は、下記が参考になります。

せん断応力とは？公式・計算法・せん断応力度との違いを解説

但し、上式の「せん断ひずみγ」は、ねじりによる影響を考慮する必要があります。「ねじりによる影響」を考えると、ねじりは、単純なせん断変形ではなく「角度の変化を伴う」ことに気づけます。下図を見てください。

丸棒に線を引きます。ABという線分です。ねじりを受けてA'B'になります。高さ方向に任意の位置Xで円周上に線を引きます。この線と前述の線分と交わる点をC、C'とします。棒の中心線O、C、C'の関係をみると、θだけ角度が生じていますね。

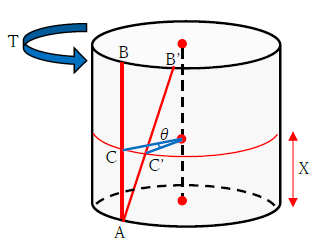
ねじりと角度の関係

Xの位置を変えると、θの角度も変わります。

Xの値が小さいほどθは小さく、Xが大きいほどθも大きくなります。

さて、X+dxの位置での角度はθ+dθです。

dxとは微小な高さ、dθは微小な角度です。

X+dxの位置での角度の関係を下図に示します。

また、元々の丸棒より半径の小さな円柱を取り出して考えます。

※見やすくするため、ｄxの高さはXと同じにしました。

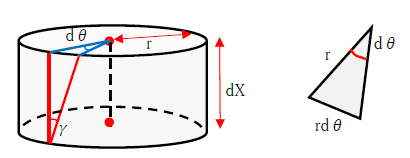
ねじりによるせん断ひずみの計算

半径ｒ、微小角度dθより、円周上の微小変形は

rdθ

ですね。半径と角度、円周の長さの関係を思い出しましょう。微小高さdxなので、せん断ひずみγは、

γ＝rdθ/dx

です。せん断ひずみを、半径、微小角度、微小高さの関係で表すことができました。せん断応力の式に代入すると、

τ＝G rdθ/dx

です。

上式をねじりモーメントT、丸棒の断面形状などを考慮し、さらに具体的な公式を求めることが可能です。結果だけ示すと、せん断応力τは

τ＝ｒ×T／J

です。Tはねじりモーメント（トルク）、Jをサンブナンのねじり定数といいます。サンブナンのねじり定数の求め方、ねじりモーメントの意味は、下記が参考になります。

鉄骨梁のねじり検討とは？ねじり定数・ねじり応力度の計算方法

ねじりモーメントとは？1分でわかる意味、公式、単位、トルクとの関係、h鋼

混同しやすい用語

ねじり（torsion）

部材の軸まわりに回転力が作用する状態。

断面にせん断応力が生じ、丸棒では外周部で最大となる。

軸力・曲げ・せん断とは異なる第4の応力状態。

ねじりモーメント（トルク）

ねじりを引き起こす力のモーメント。

単位はN・mまたはkN・m。

曲げモーメントが部材軸に直角な軸まわりに生じるのに対し、ねじりモーメントは部材軸まわりに生じる点が異なる。

ねじりを整理した表を示します。

項目	内容	備考
ねじりによる応力	断面全体にせん断応力が生じる（τ＝rT/J）	丸棒では外周部で最大となる
ねじり剛性（GJ）	せん断弾性係数Gとねじり定数Jの積	閉断面（箱型）は大きく、H形鋼は小さい
設計上の注意	構造部材はねじりが生じないよう計画・設計する	ねじりが避けられない場合は専用の検討が必要